制定系统误差分配

要测定刚体对于另一物体的相对位置，需要明确六个自由度。更复杂的是，每个自由度的误差是许多部件共同作用的结果。事实上，考虑到一个机床内所有相互关联的元件，需要掌握误差数量会非常惊人。因此，掌握和分配这些误差的允许值最好的办法就是误差分配。误差分配和其他分配一样，是指将资源分配在机械各部件上。目的是通过分配误差，使得特定部件实现误差分配的能力不会超过应有的限度。因此，最大限度地减少工作量和简化工作，满足误差分配的要求，就成为在各部件之间分配和再分配允许误差的主要目的。误差分配可以看作是控制和指导整个设计过程的工程管理工具，也是最终设计结果的预算工具。

根据定义机械各部件和连接部分运动规则，以及组合不同类型误差的组合规则，就可以制定出误差分配。确定误差分配的第一步是为系统建立一个由一系列齐次变换矩阵组成的运动学模型。接下来要全面分析系统可能产生的每种误差，并使用HTM,模型帮助确定这些误差对刀尖相对工件位置精确度的影响。然后得到一组包括所有终点误差分量、误差源以及刀尖处误差放大因子的列表。最后，应用不同的组合规则就可以得到机器总误差上限和下限的预测值。

通过误差分配检查工具端或工件位置的设计精度和规定精度时，必须首先确定机器的敏感方向。在车床上车削半径为r的圆形工件时，刀具沿着零件表面的切向运动误差为Ƹ，在工件半径方向上产生的误差大小为（Ƹ^2）/r，该误差远远小于Ƹ。如果刀具静止、工件转动，误差敏感方向固定；如果刀具旋转、工件固定，误差敏感方向跟着旋转。没有必要花费太大经历去减少那些无足轻重的误差。但通常误差分配应涵盖所有误差，以避免意外地忽视一个敏感误差，当最终列表形成后，再忽略敏感方向的误差。

机械的齐次变换矩阵模型

为了确定一个部件的误差对刀具或工件位置的影响，需要首先明确两者的空间关系。要表示三维空间中一个刚体在个体坐标系中的位置，需要一个4×4的矩阵。这个矩阵从刚体坐标系（X_n，Y_n，Z_n）到参考坐标系（X_R，Y_R，Z_R）的坐标转换，称为齐次变换矩阵（HTM）。HTM的前三列为方向余弦（单位向量i,j,k），代表刚体X_n，Y_n，Z_n三轴相对于参考坐标系的倾斜其其比例因子为0最后一列代表刚体坐标系原点相对于参考坐标系的位置P_s为一个标度因数，通常统一设置，避免混淆。上标代表称你希望显示结果的参考坐标系，下标代表被转换的坐标系。

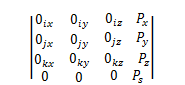
由此可得一个点在坐标系n中相对参考坐标系R的等值最标为

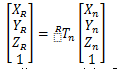
例如，当X₁Y₁Z₁坐标系沿X轴转换x，将X₁Y₁Z₁坐标系中的一个点的坐标转换成XYZ参考坐标系的HTM为

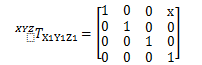
当X₁Y₁Z₁坐标系沿Y轴转换y，将X₁Y₁Z₁坐标系中的一个点的坐标转换成XYZ坐标系的HTM为：

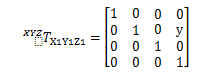
当X₁Y₁Z₁坐标系沿Z轴转换z，将X₁Y₁Z₁坐标系中的一个点的坐标转换成XYZ坐标系的HTM为：

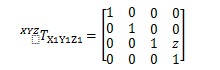
当X₁Y₁Z₁坐标系相对X轴转换⍬_x，将X₁Y₁Z₁坐标系中的一个点的坐标转换成XYZ坐标系的HTM为：

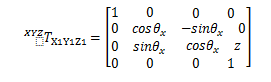
当X₁Y₁Z₁坐标系相对Y轴转换⍬_y，将X₁Y₁Z₁坐标系中的一个点的坐标转换成XYZ坐标系的HTM为：

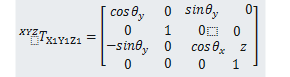
当X₁Y₁Z₁坐标系相对Z轴转换⍬_z，将X₁Y₁Z₁坐标系中的一个点的坐标转换成XYZ坐标系的HTM为：

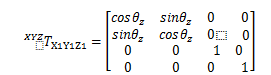
对于同时组合了这些运动的轴来说，可以将这些HTM连乘，得到一个HTM。对于较大的多维旋转来说，需要特别注意，因为旋转的方向非常重要，你可以用一本书来试验，沿不同的轴将书旋转90°，观察在旋转相同转速后，哪些面朝上。机械结构可以分解成一系列的坐标转换矩阵，描述每个轴和中间坐标系相对位置，帮助建模，从末端开始一直到基轴坐标系（n=0）。如果N个刚体被连接起来，已知相连的轴之间的HTM，那么，就参考坐标系而言，末端的位置就是所有HTM相继产生的结果

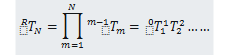
通常为零件建立刚体模型，很难确定零件的真正运动轨迹，因此，当系统中有多个接触点时，评定HTM中的误差项需格外小心。串行连接的机械需要定制的公式来说明各连接部位的相互关系。矩阵元可为数学函数，整体称为机械的成形函数，这样就产生了一个机械性能的闭型数学表示。虽然闭型方案对一些优化研究来说十分有用，但是结构复杂、轴数较多的机械来说，这种该方法通常不可取，建立的模型可能过于简单。此处所讲的HTM方法适用于任何数目的坐标系。用数学计算机就能建立出描述误差和运动轨迹的数学函数。