使用菲涅耳公式提取复介电常数和折射率，对于双相位或多相位合成是可能的，如果基质材料的杂质太小，来自系统的电磁辐射的散射可以忽略不计，胶体的研究，例如气体、液体或固体纳米颗粒的研究，在化学和物理中都有着悠久的历史，嵌入到宿主媒介的纳米颗粒的光学性质，如黄金纳米颗粒在水中的性质引起了极大光柱，由于入射光与黄金颗粒互作用时产生的表面等离子谐振，金色胶体通常呈现出红色，为了解释包含微小金属颗粒的玻璃及溶液呈现的颜色，给出了有效的媒质模型的公式表达，它包含一个主媒质和嵌入的，该模型假设没有光散射及呈球形分布的相互作用的杂质，杂质均匀分布在主媒质中，MG模型以及有效媒质模型是有效媒质的标准模型。同时也存在其他有效媒质模型，但我们主要关注这两个简单的标准模型。MG模型和B模型的基本物理属性已由Aspenes很好地进行了描述。MG模型和B模型的主要区别是B模型杂质的填充比的值不像MG模型里面那样限制得那么低，且在B模型里面填充物是嵌入在有效媒质自身里面。通常依靠复介电常数来考量有效介质模型，在MG模型汇总，双相位合成的有效介电常数如下：

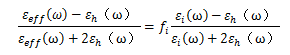
式中ɛeff是有效介电常数，ɛh是主媒质的介电常数。杂质的填充比用fi表示，当主媒质和杂质的填充比相等时，问题就出现了，因为很难确定那种材料是真正的主媒质。Bruggeman通过引入其提出的球形杂质模型解决了这个问题，即

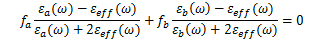
式中：a和b表明两部分有不同的复介电常数和填充比。上式可以推广到考虑球形杂质的多相结构，这些模型被推广到其他常规结构如椭圆体中，但在应用在针对一些形状不规则的复介电常数及主媒质的复介电常数决定了有效媒质的光学特性。通常，人们会观察光谱特性的变化，因为光谱特性为为填充比的函数。MG模型和B模型的缺点在于忽略了散射单元的大小。利用米氏散射理论可以修改如MG这样的模型，因此在计算有效介电常数时考虑了球形杂质的直径。对于实际情况而言，杂质显然具有不规则的形状，同时这些杂质在很多情况下是随机离散分布的，因此MG和B模型提供的有效介电常数只是一个粗略的估计。通常一种更简单的办法是利用维纳边界，它考虑两种极端情况，即所谓的微结构的最大筛查和不筛查。对于双相位合成来说这些边界可以表示为：

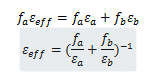
这些边界对于杂质的形状不做任何假定。维纳边界对于多相位系统说也是适用的。涉及复介电常数的系统。因为在许多情况下杂质或孔尺寸远小于太赫兹辐射波长，有效介质模型和维纳边界有时可用于太赫兹光谱定性和定量地描述系统的复有效介电常数或折射率。换句话说就是，太赫兹波的散射是可以忽略的。在太赫兹光谱范围内利用MG模型和维纳边界描述制药化合物的材料属性已有一定的进展。