抽样检测的实质是用样本属性评估总体属性。以药品为例，某批次片剂产量为一千万片，如欲知该批次产品的含量属性，将所有的产品全部检测在经济上与可行性上均不可能，只能取其中一部分样本进行检测，以样本的检测结果对该批次产品的含量进行评估。

抽样检测必然要求样本属性能够在一定程度上代表总体属性。因为在个体属性存在差异的情况下，每个样本属性均与总体属性完全一致的可能性几乎为零，因此需要评估样本属性在多大程度上代表总体属性。同样以上文提及某批次片剂含量为例，如该批次的总体含量的真实值为100%，样本检测结果不可能每次均为100%，需要确定样本的检测结果在多大范围可以接受，即确定样本检测结果允许偏离真实值的范围。

假设总体中有无穷多的个体，属性完全一致，且每次检测的结果均与真实值一致，如果抽样检测评估总体属性，样本量应为多大？

假设总体中有无穷多的个体，属性分别为1到正无穷，且每次检测的结果均与真实值一致，如果抽样检测评估总体属性，样本量应为多大？

以上是总体属性的两种极端情况，显而易见，第一种情况可以选择任何大小的样本，即样本量最小可以为1；第二张情况样本量越小，检测结果与总体均值不一致的风险越大，样本在容量无限趋近于总体的时候，其属性无限趋近于总体，即样本越大，其属性越接近总体属性。但出于经济、可行性等方面的考虑，样本量一般不宜过大。

通过上文的假设，能对样本量有了一些直接的感性认识：

样本量与个体间的偏差成正相关，偏差越大，样本量越大。完全均匀的总体，样本量可以任意小。

样本量与检测结果允许偏离的范围成负相关，允许偏离范围越小，样本量越大。

样本量与允许OOS的次数成负相关，允许OOS的次数越少，样本量越大。

样本量除了个体间属性的差异外，还需考虑检测本身产生的误差，如仪器响应、称量、稀释等。

根据置信区间理论，假设总体均值为μ，标准误差为σ，则样本量为n的样本均值`X的置信区间为：

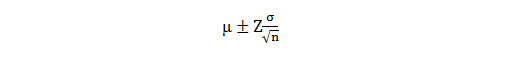
Z值可通过查询Z值表查得。

如样本检测结果允许偏离总体均值的范围为k，即：

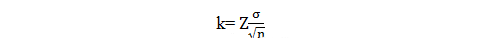
该公式可变形为：

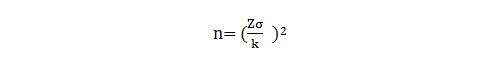
该公式可以解释上文提及的样本量的感性认识，Z值与置信系数（可以理解为允许OOS的次数）相关，σ为个体间的偏差，k为允许偏离的范围。样本量与三个参数均呈2次方关系，也就是每个参数的影响均非常巨大。

同样以上文提及某批次片剂含量为例，如该批次的总体含量的真实值为100%,σ为10%，检测结果的可接受区间为98.0%~102.0%，允许OOS的次数是每千次检测出现1次，则样本量应为多少？

查询Z值表中置信水平0.999的Z值，Z=3.1，代入公式计算，n=240。

如σ为2%，样本量应为多少？计算可得n=10

由此可看出个体间的均匀性对样本量的影响之大。

在方法开发的实践中，一般无法获得用于方法开发的样品的μ与σ值，一般只能通过检测获得样本的平均值与标准差s，可通过样本的置信区间

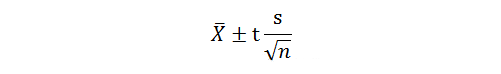
同上文的原理进行评估。

需要注意的是，实践中检测结果变异的来源并只是样本不均匀导致，还包括方法、仪器、操作及其他，这些来源的变异并不能通过增加样本量的方式减轻；一般应当优化分析方法，如改进色谱条件使峰型更加对称减少积分误差、避免溶剂效应对响应值的不利影响等；也可增加平行测定次数以减少误差。如何操作应当根据检测结果允许的偏离范围以及相关误差的大小综合判断。如原料药，一般情况下可认为样本是均匀的，其检测结果变异均为其他来源。

以HPLC法片剂含量测定为例，如对照品连续进样5次的RSD为0.3%，分别测定10片，含量结果的RSD为3%，这表明检测结果变异的主要来源是样本的均匀性，可根据上述原理评估含量测定的样本量。

由于篇幅有限，为减少非样本均匀性导致的检测结果变异、增加平行测定次数的研究方法将另作说明，本文不再论述。