一、引言

 

在产品的寿命分析及预计研究中，需要用到各种寿命分布函数，主要包括：正态分布函数、对数正态分布函数、指数分布函数、威布尔分布函数等。其中，指数分布是用来描述电子产品在随机失效阶段的可靠性函数，在可靠性领域中研究甚为广泛。然而，由于产品自身的复杂性、产品所处阶段的不确定性等因素，我们在处理产品试验数据、现场使用数据、产品售后数据时，并不能完全确定产品所处的浴盆曲线阶段，与此同时，很多产品由电子件及机械执行件构成，仅仅利用指数分布进行数据耦合是远远不够的。基于此，威布尔分布在产品的寿命分析中可以起到重要的作用，威布尔分布中的形状参数取值不同，可以产生不同的函数形态，函数形态可以对应不同的产品失效阶段；威布尔分布中的尺度参数可以在确定函数形态后对函数进行拉伸，可以对应产品的失效速率进行耦合描述；威布尔分布的位置参数，又可以将函数的初始位置进行平移，可以对应描述某些产品通过一段“货架期”后进入寿命阶段的特性。

 

本文将细致介绍威布尔分布函数对应的失效密度函数f(t)、失效函数F(t)、失效函数；威布尔分布函数的形状参数、尺度参数和位置参数的含义，参数的变化可以形成不同的失效函数形态产生不同的函数类型；威布尔分布函数的三个参数如何通过双对数方式及线性回归方式进行求解，从而估计产品的各种寿命，为产品制定保修期、售后等提供依据。

 

二、威布尔分布的失效密度函数、不可靠度函数、失效函数及各参数含义

 

1、威布尔分布的相关函数形式

 

 

2、威布尔分布各参数含义

 

自变量t含义：在不同的场合中可以有不同的意义，比如时间、距离、（试验）循环或机械应力等等。

 

形状参数β含义：形状参数是瞬时失效率随时间的变化率。例如：早期失效、随机失效、耗损失效。形状参数决定了该分布是威布尔分布族中的哪一种。形状参数不同的威布尔分布密度函数的形状是截然不同的。这就使得威布尔分布与其他分布模型相比，能够拟合很多的寿命数据。形状参数起决定性作用，决定函数形状即产品所处的失效阶段，在不同的参考文献中记录为不同的字母，读者只要记住在威布尔分布的各函数中，幂指数位置的参数为形状参数即可。因为幂指数在整个函数中级别最高，驱动效应最强，此位置的参数为最为重要的形状参数。

 

尺度参数η含义：尺度参数变化影响失效率增长速度，η越小，增长速度越快。尺度参数起到拉伸整个函数的作用，对于产品失效而言体现为失效速率的快慢问题。

 

位置参数t0含义：利用位置参数，失效时间平移了一段固定时间（t0），这个固定时间称作“门限”。当产品先度过一段“货架期”才可能发生首次失效时，通常这段时间可以作为位置参数。如果威布尔概率图有凹凸形状则提示需要加入位置参数。很多时候产品出货后即应用，进入寿命期，此时t0=0，这时威布尔分布即变换成为两参数分布。位置参数会改变失效率函数的左右位置（即起始位置的改变），不会引起函数曲线形状和大小的变化。

 

下面通过数形结合的方式更直观的描述各参数在寿命分布中的意义：

 

 

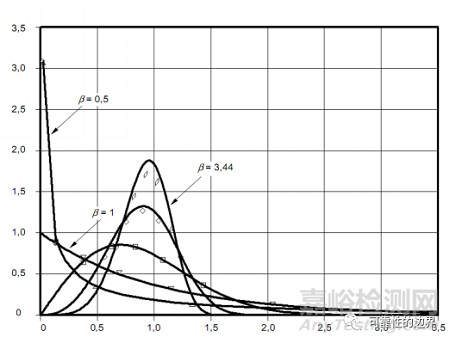
图1：尺度参数η=1，位置参数t0=0时威布尔分布族的失效密度函数形状

 

从图1中可以看出，当形状参数β=3.44时，威布尔分布的概率密度函数（PDF）看起来很像正态分布，实际上它除尾部外都与正态分布十分相似；当形状参数β<1时(图上为0.5)，失效密度函数没有峰值，直线t=t0是它的一条竖直渐近线；当形状参数β>1时, 失效密度函数先增后减。

 

 

 

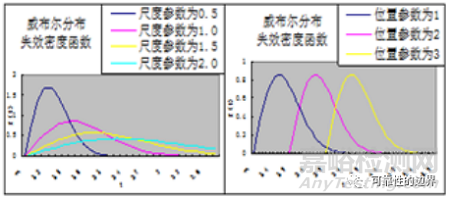
图2：威布尔分布失效密度函数图形（尺度参数、位置参数对时效密度函数作用）

 

从图2左边第一张图中可以看出，当形状参数一定，位置参数为0时，尺度参数的作用是拉伸失效密度函数，尺度参数越大，失效函数上升越慢，下降也越慢；从图2第二张图可以看出，位置参数的作用相当于将失效密度函数右移动，实际的意义为：早期（即右移的一段）产品不失效。

 

 

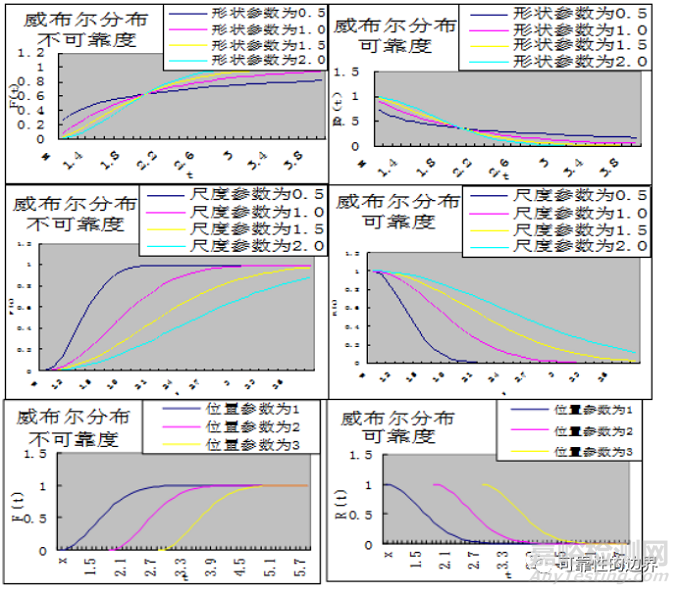
图3：威布尔分布可靠度与不可靠度函数图形（形状参数、尺寸参数、位置参数比较）

 

从图3的6张图中，显而易见的看出，形状参数越大，可靠度起始水平高，但可靠度随时间下降快（即形状参数越大，不可靠度（失效）起始水平低，但可靠度随时间上升快）；尺度参数越大，可靠度下降越缓慢（即尺度参数越大，不可靠度（失效）上升越缓慢）；位置参数的加入，使得产品存在一个无失效时间（即产品过了位置参数时间后才开始失效，前面时间全部完好）

 

 

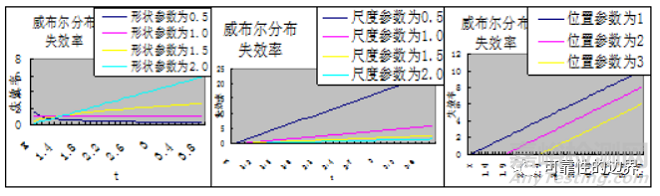
图4：威布尔分布失效率函数图形

 

从图4的3张图中，可以看出，形状参数，决定了失效率的上升、下降或恒定；尺度参数决定了失效率的快慢；位置参数决定了起始失效位置。

 

对于形状参数对失效率的影响作如下总结：

 

当β=1，威布尔分布就是指数分布；

 

当β>1，威布尔分布的瞬时失效率随时间递增；

 

当β<1，威布尔分布的瞬时失效率随时间递减。

 

3、威布尔分布小结

 

通过上面的分析，我们认识到威布尔分布的变换形式是多样的，通过不同的参数变换可以变换成不同形式的分布模型，例如：指数分布、正态分布等。与此同时，对于产品的早期失效、随机失效、耗损失效都可以进行描述。

 

基于此种特性，我们需要进一步研究，如何通过一系列的产品数据，求解出威布尔分布的各参数，从而进一步推算产品的各种寿命指标。

 

三、威布尔分布评估产品寿命指标分析

 

1、整体思路

 

通过威布尔分布分析产品寿命的整体思路是，利用上面分析的不可靠度函数。

 

 

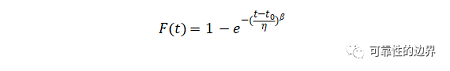
通过产品的故障统计，利用线性回归的方式将产品的每个故障时间t、计算出的每个故障的不可靠度F(t)组成回归方程，将形状参数、尺度参数及位置参数求解出。从而就可以利用不可靠的函数，计算产品的各种寿命指标。

 

2、寿命指标

 

常用的寿命指标有B10、B20、中位寿命（B50）、MTBF(MTTF)等。用户可以根据自己的需求制定符合自己企业需求的寿命指标。

 

B10:作为考察的一批产品从投入使用至10%的产品损坏所经历的时间。利用上述F(t)=0.1,反解出时间t即可。同理可知道B20及中位寿命即B50含义及具体求法。 

 

MTBF(MTTF):平均无故障间隔时间。从威布尔分布失效函数的角度解释为，当产品工作时间t达到特征寿命η时，这时的产品失效率为63.2%，MTBF(MTTF)就是特征寿命η。MTBF(MTTF)为经常使用的寿命指标，是否合适此处不讨论，读者可以根据需要选择。

 

读者可以根据自己的产品需要，选择其它的寿命指标。

 

3、数据来源

 

威布尔分布耦合的寿命数据可以从多方面获得，（1）通过可靠性试验，统计产品数量、试验时间、故障数；（2）现场使用数据，统计使用时间、故障数、产品数量；（3）售后数据，统计返修时间、故障数、故障产品数量。

 

威布尔分布的数据处理可以渗入到产品的各个阶段，应用广泛、实用性极高。

 

4、本文实例数据来源

 

本次实例数据来源于某厂家生产的汽车显示屏产品，随机抽取201件研究其使用可靠性。通过显示屏的返回车厂维修数据进行统计，统计数据见表1。（篇幅考虑，截图部分数据示例）

 

 

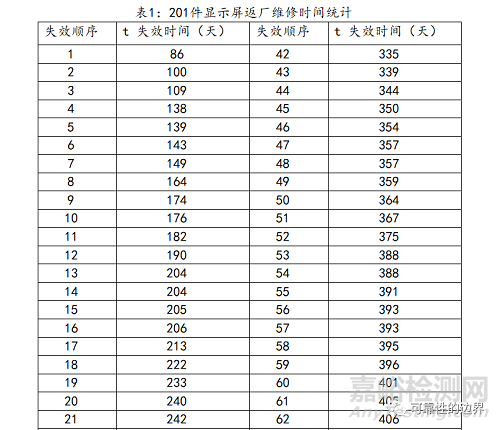
5、中位秩法计算不可靠度F（t）

 

中位秩计算F(t)，此处简单介绍计算方法，需要详细了解例如：删失数据、搁置数据、调整秩的读者可参考IEC61649标准或相关资料。

 

 

6、不可靠度F（t）的双对数表示方法

 

为了线性回归的需要，需要将F(t)变形为Y=AX+B的形式，此处的方法为取两次对数，这样就可以将指数部分放下，便于后续数据处理。变形方式很多，笔者采用相对简便的一种进行变换。

 

 

7、利用最小二乘法求解线性回归方程中的A和B

 

利用上面的双对数式，中位秩算法，可以连列出表1的矩阵方程组，利用最小二乘法可以方便计算出A,B的值。此处只列出A，B算法，不对最小二乘法做探讨，有兴趣读者可参考其它资料。

 

 

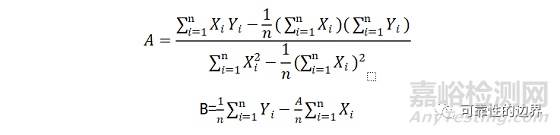
8、本案例求解

 

本案例中，产品个数一共为201(即n=201),表1中已列明，时间t以天为单位，失效序列也列明，可以方便求出对应的不可靠度，由于产品出货即应用，没有“无失效的货架期”，故此例中位置参数。下面笔者通过上述方法，用电子表格的方式对形状参数β、尺度参数η进行求解,详见表2。（篇幅考虑，截图部分数据示例）

 

 

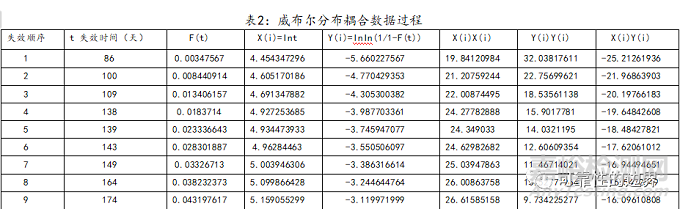
9、产品寿命指标估计

 

根据上述求解出来的形状参数（β=1.98687816）和尺度参数（η=756.5491009），不可靠度函数可写成：

 

 

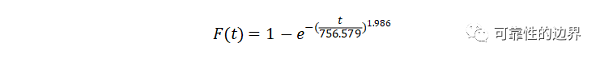
产品工作到756天左右，即特征寿命时，约有63.2%会产生故障，此产品的使用MTBF(MTTF)约为756天；B10寿命，F(t)=0.1,反解出t，可方便求出B10约为242天；同理可计算出，B20约为354天，B50约为628天等等。

 

四、结束语

 

对威布尔分布的研究目的是为了评估产品各种寿命指标，用户可以根据自己产品的试验数据、现场使用数据、返修数据等归纳自己产品的故障类型，不同故障的时间序列，利用威布尔分布对其进行耦合，从而科学的得到在现有水平下，某类产品的故障产生概率大小，及早制定维修、保障计划，节约公司成本，同时对于反映出的重点问题，可以进行识别从而加以改进。利用这种数据处理手段同样可以将试验及现场数据进行分析，得到更好更符合实际的试验方案。

 

对于本文讨论的威布尔分布寿命分析，通过工程化的实用算法为产品解决数据评估问题，但其中并未涉及置信区间的讨论，因为威布尔分布的置信区间讨论的方法很多（例如极大似然估计、矩估计等等），也比较复杂，本文出于方便工程实践角度，不予讨论。但这并不影响对此数据的采纳与使用，例如上述的寿命指标可以人为规定一个5%-10%的波动区间，这也是符合实际需要的。