针对定时截尾试验中装备无失效被接收时平均无故障间隔时间（Mean Time BetweenFailures, MTBF）估计的问题，通过一种简易的方法从理论上推导得出了无失效情形下MTBF置信下限的计算公式，并与其他方法进行了比较。同时根据置信下限计算的公式分析出一种定时截尾试验点估计的实现方案。最后通过实际工程应用，验证了方法的有效性。

随着军方对装备可靠性的重视，装备的设计不断更新优化，相应配套元器件的可靠度也在逐渐提高，在进行可靠性鉴定和验收试验时出现零失效被接收的情况是越来越多。

然而，在MTBF值的实际验证过程中，当失效数大于0时，根据GJB 899A-2009《可靠性鉴定和验收试验》提供的方法可以很方便的计算出MTBF的估计，但对于失效数为0时的情况，标准中没有给出明确说明。

对于这一问题，有文献从应用数学的角度推导出了指数分布下失效数为0时MTBF置信下限的计算公式，理论性较强，对工程人员来说理解起来需要花费精力。本文给出了一种简易的推导方法，并对MTBF的点估计做了初步探讨，给出了一种计算公式。

失效数为r(r>0)时被接收的估计

根据GJB 899A，当做出的试验判定为接收时，该试验停止前发生的责任失效数一定小于等于接收判决的失效数，试验必须是在达到规定的试验时间后就停止的。

即MBTF的点估计  为：

（1）

式中：

T—装备的总试验时间；

r—责任失效数。

置信度为C的MTBF验证区间为(θL，θU)，其中θL为置信下限，θU为置信上限。计算公式为：

 （2）

  （3）

其中C’=(1+C)/2为单边置信限的置信度，θL(C’,r)和θU=θU(C’,r)分别为置信下限系数和置信上限系数。计算公式为：

  (4)

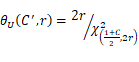(5)

标准中给出了取置信度C=1-2β（其中β为使用方所承担风险）时，失效数大于0情况下的置信下限和置信上限系数。通过查表就可以计算出MTBF的验证区间。但是当失效数为0时上述方法无法应用。

失效数为r(r=0)时被接受的估计

01、MTBF置信下限的推导

任取n个失效率为λ的指数型样品做定时截尾试验，则到试验截止时间t时已失效k个的概率服从二项分布为：

（6)

因此，到时间 t时，已失效的样品数k≤a（k为试验方案中规定的接收失效数）的概率就是装备被接收的概率，公式为：

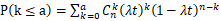(7)

当n比较大，λt比较小时，可以用泊松概率近似该二项概率，此时装备被接收的概率可以近似表示为：

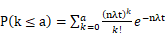  (8)

对于有替换的试验总试验时间T=nt ，对于无替换的试验，由于k相对于n来说较小，近似取T=nt，则：

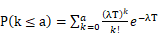（9）

由此可得试验方案中MTBF的真值θ与接收概率P(θ)的关系为：

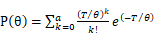(10)

由于β为使用方风险，即当实际的θ=θ1（θ1为检验下限值）时，装备被接收的概率，代入上式有：

   (11)

当达到截止时间，失效数为0时，代入上式得：

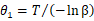
对于θ1满足

根据单侧置信限的定义，此时称θ1为置信度为1-β的单侧置信下限，记为θL,即：

  (12)

该公式与相关文献推导出来的公式是一致的，区别在于部分文献推导过程理论性比较强，工程试验人员理解起来比较困难，不易掌握，而另有文献是基于失效数不为零的情况下进行的推导，不具备较强的说服力。

02、无失效时的点估计

当达到试验截止时间，责任失效数为0，做出接收判决时，GJB 899A中没有给出MTBF点估计的计算方法，而GB5080.4-85《设备可靠性试验可靠性测定试验的点估计和区间估计方法（指数分布）》 中则给出了推荐公式，即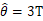，但应用此方案需要使用方承担很高的风险。

针对此问题， 由于MTBF点估计值在不同置信水平C下存在于真值θ与检验下限θ1之间，通过式(12)可以推断，此时必有一估计下限θ1’使得

(13)

取 θ1’作为无失效时MTBF的点估计，则

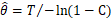   (14)

若采用GJB 899A中建议的置信度 C=1-2β，则

 (15)

不同 β值下的点估计见下表1。

表1. 不同 β值下的点估计

根据式（15）的单调性，可知β 越大越大，当β=0.3时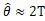，，相对于GB 5080.4推荐的图片，有效控制了使用方风险。

案列分析

某型北斗车载终端要求的MTBF最低可接受值为θ1=160 h ，在定型阶段的可靠性鉴定试验中，通过对该终端全寿命周期分析，确定了其不同的任务剖面，再参照其每一种任务剖面的特征参数图，拟定出了其在该任务剖面下的环境剖面，参考标准对环境剖面数据简化后形成制式表格，最终绘制出了针对该终端的试验剖面图。根据试验大纲要求采取定时截尾试验验证，选用标准GJB 899A中标准型试验统计方案17进行本次试验，总试验时间为。

试验结束后，对统计的试验数据进行整理分析，责任故障为零，结果为无失效，对该终端给出的判定为接收。

依据技术文件要求，在形成正式报告时需要对该型终端的可靠性指标进行估计，由于提供的技术文件中没有对无失效接收时的点估计进行明确约定。与相关技术人员进一步沟通后了解到该型号技术还不尽完善，成熟度可能不高。于是议定采用式（15）计算点估计得。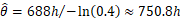

由于试验结果为无失效，在获得MTBF验证区间时只需计算其置信下限，依据式（12）得。

针对本次试验，对于点估计的计算，如果依据GB 5080.4推荐的公式计算可以得到，此计算结果远大于750.8h，这个数据对于使用方了解装备可靠性是没有指导意义的。当装备成熟度比较高时，可以参考引用。

结  束 语

随着使用方对装备可靠性要求越来越具体化，针对可靠性验证试验中无失效被接收的情况，只对试验结果进行接收判定已不能满足使用方要求。本文从装备被接收的概率公式出发，考虑当样品无失效时这一特殊情况，对概率公式进行简化，进一步从理论上推导出了MTBF的置信下限及点估计公式，通过案例借用推导的公式对试验结果进行了定量分析，有效的帮助了使用方对装备可靠性的直观了解，得到了生产方和使用方的认可，同时为工程试验人员提供了一种可行的实施方案。