确信可靠性理论基于三个科学原理，建立了4个方程，通过求解这4个方程，可以优雅地开展以确信可靠度为目标的产品正向设计。确信可靠性理论的核心思想有：

（1）科学原理

可靠性的本质是确定性与不确定性的综合体现。首先，可靠性是一个确定性的问题，它是由产品的裕量（性能与阈值的距离）和退化规律决定的。裕量越大，退化越慢，产品越可靠。其次，可靠性又是一个不确定性的问题，各种不确定因素将共同影响裕量与退化的大小和趋势。确信可靠性理论由此总结出以下三个科学原理：

原理1.裕量可靠原理：产品的裕量决定了其可靠程度；

原理2.退化永恒原理：产品的裕量始终沿着退化时矢发生退化；

原理3.不确定性原理：产品的裕量与退化过程具有不确定性。

裕量可靠原理指出了人们对产品最基本的要求，裕量越大意味着产品完成规定功能就越轻松；退化永恒原理指出了产品运转的客观规律，从无限长的时间尺度看，产品一定处在退化中；不确定性原理指出了人类实践的矛盾要素，人们不仅需要把握裕量和退化的确定性规律，还要衡量各类不确定性的影响。

（2）数学表达

在可靠性科学原理的指导下，确信可靠性理论给出了四个基本方程，并将规定时间、规定条件和规定功能全部纳入了可靠度函数中。

其中，P为性能参数向量，X为产品内因变量（如材料、尺寸），Y为产品外因变量（如环境条件），t为退化时间，M(t)为裕量向量，Pth为性能阈值向量，R(t)为可靠度函数，为度量不确定性的某种数学测度。

学科方程是不同学科领域中基本科学原理决定的方程，它描述了产品关键性能与设计变量、外界环境应力变量之间的函数关系，例如电子产品的电性能方程、机械产品的力学方程等。退化方程描述了关键性能随时间变化的函数关系。裕量方程表征了性能参数与性能阈值之间的距离。度量方程是对“裕量大于0”这一事件不确定性的量化，需要根据实际需求确定数学测度，从而完成可靠性度量。

可以看到，关键性能参数及其裕量要求体现了产品的“规定功能”，退化时间体现了产品的“规定时间”，内外因变量则体现了产品的“规定条件”。因此，基于四个方程得到的可靠度函数才真正覆盖了可靠性定义的所有要素。

（3）实验验证

确信可靠性理论强调应通过开展可靠性科学实验来验证和揭示产品裕量与退化的确定性规律。

确信可靠性理论中提出的可靠性科学实验主要包含两大类：功能可靠域实验与性能退化律实验。

功能可靠域实验通过不断提高产品环境应力或工作应力的方式，获取产品功能边界、性能阈值或极限应力，从而验证产品裕量大小。

性能退化律实验通过开展产品内因和外因变量不同组合下性能的退化实验，探究产品的退化轨迹和敏感因素，从而验证产品退化过程。

（4）机会预测

确信可靠性通过度量方程来实现可靠度的预测。那么其中数学测度如何选择呢？确信可靠性理论给出了最一般的形式——机会预测，即通过机会测度量化可靠性水平。

机会测度Ch是概率论中的概率测度和不确定理论中的不确定测度的融合测度。当能够收集到足够的故障数据时，产品称为随机系统，机会测度退化为概率测度；当面对小样本数据时，产品称为不确定系统，机会测度退化为不确定测度；当同时出现两种情况时，产品称为不确定随机系统，则直接使用机会测度。

基于这一分析，确信可靠度就被定义为系统裕量大于0的机会，即：

RB(t)=Ch{M(t)>0}

这一定义包含两方面内涵：一是裕量可以是狭义的性能裕量，如电性能裕量、机械性能裕量，对应基于性能裕量的确信可靠度，通常用来开展确信可靠性设计、分析与实验。二是裕量可以是时间裕量，如故障时间裕量、服务时间裕量，对应基于时间裕量的确信可靠度，通常用来开展确信可靠性评估。确信可靠度的两个内涵对应着不同的工程应用场景，可以在不同背景下开展合适的可靠性工作。

确信可靠性理论的数学基础是概率论、不确定理论和机会理论，围绕确信可靠度这一核心，形成了完整的可靠性度量体系——确信可靠性度量框架，如下图所示。

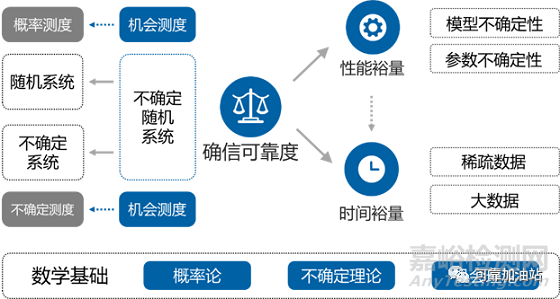
目前，确信可靠性已形成了较为完整的理论和方法体系，建立了全新的可靠性理论话语。这一创新的理论成果在工业界得到了广泛关注。