有同行提出问题，在扫频试验中，扫频速度2oct/min，频率范围5～1000Hz，来回往复扫频，扫频试验时间为60min，问试验结束时的频率是多少Hz？

要想计算此结束频率，需要先复习倍频程的概念，

倍频程（oct）

※定义

    指使用频率f与基准频率f0之比等于2的n次方，即f/f0=2n，则称f为f0的n次倍频程。计算式如下，

      n = lg（f/f0）/lg2 或  n = log2（f/f0）

比如，下限频率100Hz，上限频率2000Hz,通过上面的计算式可以得到100～2000Hz之间约有4.3个倍频程（可以简写成4.3oct）。

回到问题，将此概念充分理解，反向应用，便可计算出问题的答案。

第一步，

下限频率5Hz，上限频率1000Hz，则利用上面计算式得到该频率范围内有n个倍频程（小数点后取5位）。

    n = lg（1000/5）/lg2 = lg200/lg2 = 7.64386 oct

第二步，

从5Hz到1000Hz扫频，扫频速度2oct/min，所以，频率范围内扫频一次的时间是，

7.64386oct ÷ 2oct/min = 3.82193min

第三步，

扫频试验时间为60min，可以计算出一共扫频的次数为，

        60min ÷ 3.82193min = 15.69887 次

第四步，

来回往复扫频，可推算出最后一次的扫频方向为从大到小，如下图所示，

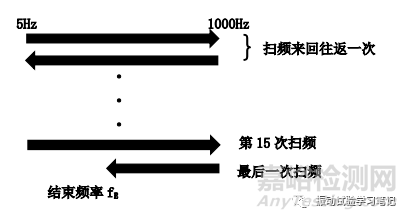
最后一次扫频为0.69887次，花了3.82193min×0.69887= 2.67103min，也就是扫了2.67103min×2oct/min= 5.34206oct。

第五步，

也就是结束频率fE到1000Hz有5.34206oct，反向利用倍频程计算公式，即（小数点后取2位）

lg（1000/fE）/lg2  = 5.34206

lg（1000/fE）= 5.34206×lg2

1000/fE= 101.60812

fE= 24.65 Hz

也可以用另外一种方法，fE到1000Hz有5.34206oct，则5Hz到fE有

7.64386- 5.34206 = 2.3018 oct

即（小数点后取2位）

lg（fE /5）/lg2 =2.3018

fE/5 = 100.69284

fE = 24.65 Hz

（小数点后面位数不同，结果会有所偏差，以振动控制仪内的数据结果为准。）

（扫频方向（频率来回往复、频率从大到小、频率从小到大）不同，结果也不同，可自己分别计算一下。）

总结

  这是一个很好的问题，一般试验中，都是通过振动控制仪输入试验条件，自动生成扫频数据，不会去深入计算结束频率。之所以撰文，主要是为了帮助初学者理解倍频程（oct）的概念，随机试验条件PSD中也经常会出现倍频程（oct），比如oct/dB。