实际工程应用中，通常会在实体模型表面包一层很薄的壳单元，这是为什么呢？

先说答案：实体网格表面包壳可以提高表面应力精度。

下面通过一个存在理论解的一侧受集中力的悬臂梁案例来详细解释。

1、理论解

有如下所示的悬臂梁，长L=1500mm，宽b=20mm，高h=100mm，杨氏模量210GPa，泊松比0.3，一端受力F=1000N。

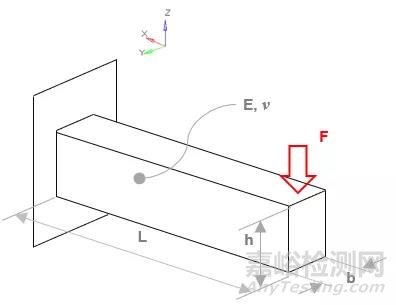
悬臂梁受集中力示意图

根据材料力学相关内容，可得出理论解：全局最大位移为3.214mm，L/2截面内最大应力为22.5MPa。

2、仿真结果

2.1 位移对比——包壳vs不包壳

网格密度6x1x1表示L方向网格分6层，h和b方向网格分1层。下图为不同网格密度下，二阶四面体网格模型表面包壳和表面不包壳的位移结果对比，一共6个模型，上面三个模型表面不包壳，下面三个模型表面包一层厚度为0.0001mm的与实体单元材料相同的钢片。

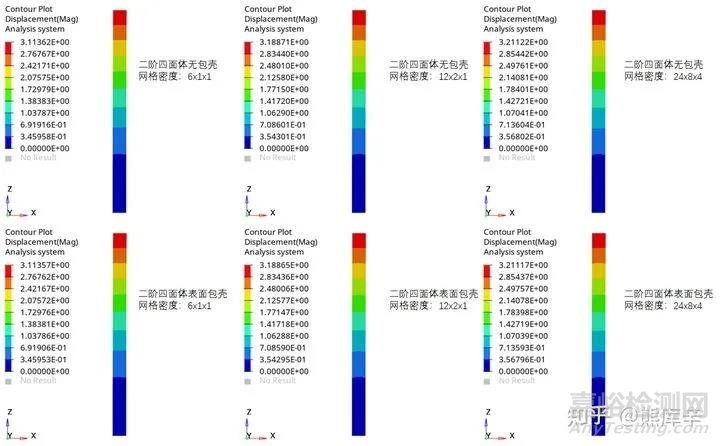
位移对比——不同网格密度/包壳和不包壳

可以看出，6个模型中位移都与理论解非常接近，同一列的两个模型网格密度相同，其位移差异非常小，包壳的模型表面加了一层材料，因此其位移比不包壳的模型位移略小，但几乎可以认为包壳对于位移完全没有影响。

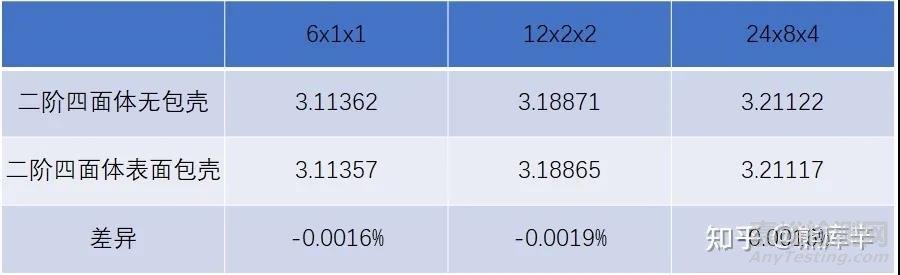
位移对比——不同网格密度/包壳和不包壳

2.2 应力对比——包壳vs不包壳

下图为不同网格密度下，二阶四面体网格模型表面包壳和表面不包壳的位移结果对比。一共6个模型，上面三个模型表面不包壳，下面三个模型表面包一层厚度为0.0001mm的与实体单元材料相同的钢片。

应力对比——不同网格密度/包壳和不包壳

备注：上图为根据积分点应力进行插值平均得到的结果

根据上图和下表可知，不同网格密度下，包壳和不包壳的模型L/2截面处最大应力差异非常大，包壳模型L/2截面上最大应力更接近理论解22.5MPa；随着网格不断加密，仿真模型应力逐渐接近理论解，包壳和不包壳模型的应力差异逐渐减小；表面包壳时，即使网格使用比较稀疏的网格，可也可得到相对准确的结果；网格足够密的情况下，包壳和不包壳模型的最大应力将完全一样，没有任何差别。

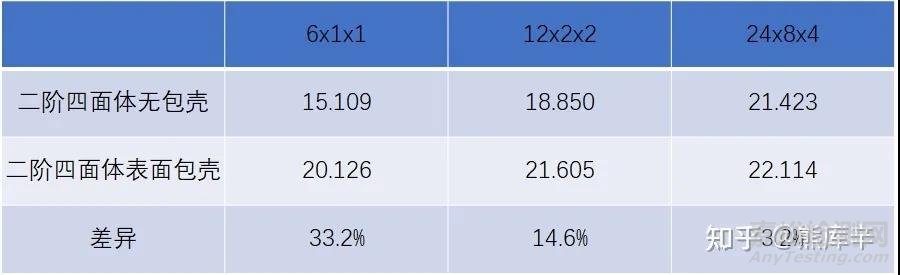
应力对比——不同网格密度/包壳和不包壳

根据上述对比，可以得出结论：二阶四面体网格表面包一层薄壳，其应力更加接近理论解.

3、理论说明

表面包壳为什么应力更准确呢？

先了解一下应力计算流程。

有限元求解器首先根据平衡方程 图片 求出节点位移矩阵X，然后根据节点位移求解积分点上的应变，再根据物理方程 图片 求解积分点的应力。有限元求解器只计算了积分点上的应力，后处理器根据积分点应力插值得到整个单元内所有位置的应力并以云图的形式进行显示。

一阶四面体网格只有一个积分点，在单元中心位置；二阶四面体单元共4个积分点，在单元内部接近节点的位置，具体位置如下图所示。

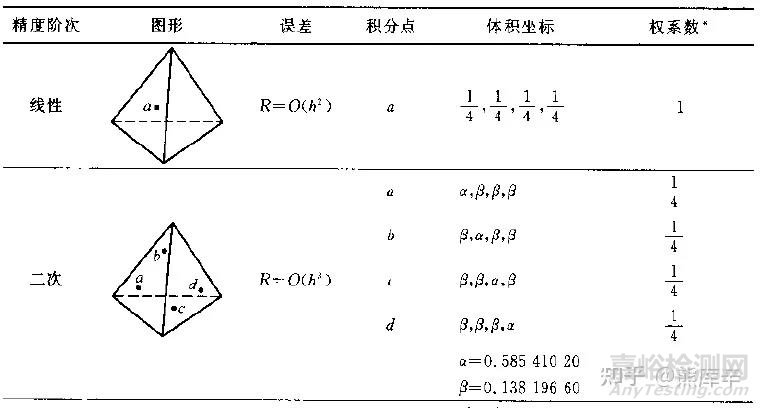
四面体单元积分点位置示意图

实际模型的最大应力通常在表面。

若使用四面体单元，表面不包壳，则由单元内部的积分点向表面插值得到模型表面应力；积分点在单元内部，即在模型内部，向模型表面插值时存在一定误差；

若模型表面包一层薄壳，即有一层三角形壳单元，由于壳单元本身就在模型表面，即三角形壳单元的积分点也位于模型表面，因此根据三角形壳单元计算得到的表面应力更准确。

存在弯曲变形的情况下，厚度方向的应力梯度会明显大于零件表面面内的应力变化梯度，也从另一方面印证了通过包壳插值得到的应力精度高于通过四面体单元进行插值的应力。

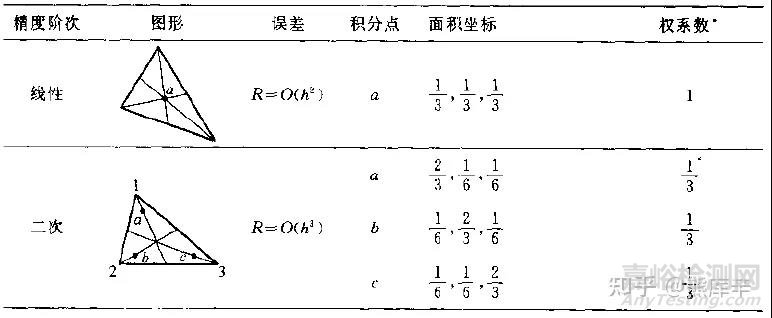
三角形单元积分点位置示意图