材料力学的研究对象为细长结构，其几何特征在一个方向上的尺寸远大于另外两个方向，如方柱、圆柱、多边形柱、长杆、梁、轴等，都属于材料力学的研究对象。细长结构是大自然中存在最为广泛的结构之一，也是人类最早认识和使用的典型结构之一。

在人类早期的工具中有许多属于细长结构，如棍棒、骨针（图1(a)）以及石刀、石斧、石矛的把等，许多复杂结构也多利用细长结构搭建而成。早在农业文明早期，人们已经学会利用树枝搭建帐篷，一般用几根树枝搭成穹窿，周围抹上泥土或搭上兽皮、树叶等成为人类最早的建筑（图1(b)）。因此，与细长结构相关的力学问题也最先被提出来，成为典型的力学结构，在工程中得到了广泛的应用。

图1

在材料力学中，根据细长结构的受力特点，可认为材料力学只研究杆、轴、梁三类典型结构。杆是指承受轴向拉力或压力的构件，轴是指承受扭矩的构件，梁是指承受弯矩（一般情况下还有剪力）的构件。材料力学中，杆、轴、梁的概念虽然来源于工程，但并不等同于工程中的概念。

例如，本来承受轴向压力的“柱”，如果发生倾斜后，其在内力上将会产生弯矩，此时的柱就兼有了“梁”的受力特征；又如承载火车车厢的车轴，当其不做动力轴时，在车厢重力作用下，轴发生弯曲，在力学上也具有“梁”的受力特征。可见，材料力学中的杆、轴、梁实际上是依据细长结构的内力特征而提出的力学模型，它们并不等同于工程概念中的杆、轴、梁。

必须注意到，材料力学主要以细长结构为研究对象，以细长结构的内力为研究手段，以细长结构的强度、刚度、稳定性为研究目标。但也应注意到，工程中除了细长结构，还有许多结构不是细长结构，如楼板、储气罐、大坝、隧道，乃至更加复杂的异形结构，对于这些非细长结构应该如何确保它们的服役安全呢？这些问题的解决就促成了弹性力学对材料力学的批判和继承。

首先，弹性力学批判了材料力学只能研究和分析细长结构的不足。弹性力学以微元体为研究对象，微元体以弹性体中的任意点为基准，在空间维度上沿x、y、z 三个方向分别延伸三个微量△x，△y，△z，形成六面体微元，如图2所示。显然，利用微元体可以搭建出任意形状的工程构件。只要求出微元体的应力、变形量，再令三个微量△x，△y，△z 都趋近于0的时候，微元体上的应力、变形量就成了该点处的应力和变形，依据这些应力和变形就可以确保弹性体在特定载荷和变形状态下的服役安全。因此，弹性力学以微元体为研究，就为工程问题提供了一种底层思维模式，通过微元体，解决任意结构形式受力和变形问题。

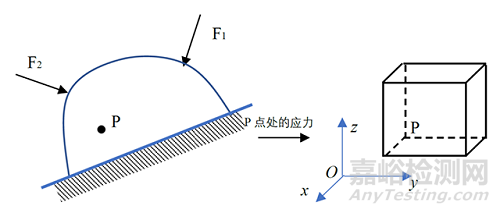
图2

其次，弹性力学对材料力学的批判还体现了基本概念上，如应力、应变、位移、外力等。虽然这些概念在材料力学中学习过，但弹性力学扩展了这些定义的内涵，以下依次说明。

1. 应力在材料力学中定义为单位面积上的内力，如图3所示。

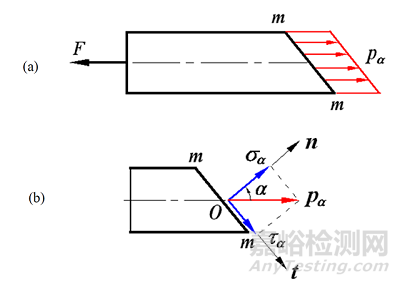
图3

图中，pα表示任意截面上的全应力，可分解为垂直于截面的正应力σ 和平行于截面的剪应力τ，设Aα 为任意斜面的面积，则全应力可通过下式求得

这个公式看起来很像压强的公式，事实上，应力的概念就是欧拉 (Leonhard Euler, 1707-1783) 于1752年借用流体压强的概念来理解固体材料内部压力而提出来的。后来，柯西 (Augustin Louis Cauchy, 1789-1857) 考虑材料内部的应力分布并非均匀分布，在欧拉应力概念的基础上给出新的应力定义，现在成为了弹性力学中的应力定义。如图4所示，设P 点是的弹性体内部一点，过P 点做一个微面，设其面积为△S，当该微面上所受的力为△P，则该截面上的全应力p 可定义为

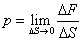
图4

更进一步，柯西所考虑的微面是任意方向的微面。如图5所示，以P 点为基准，在x、y、z 方向上分别产生增量△x、△y、△z，连接ABC组成的任意微面，当△x、△y、△z 均趋近于0时，△S 也趋近于0，就可以通过上式求得过P 点任意截面上的应力分量。

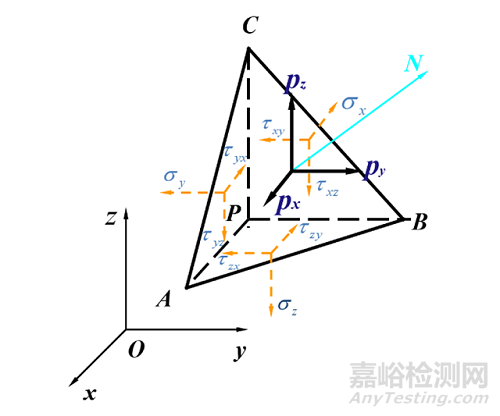
图5

2. 在材料力学中的线应变ε 也被定义为杆件结构上单位长度的改变量，用以衡量杆件的变形能力，其表达式如下

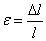
其中，l 表示线段的原始长度，△l 表示杆件在变形后的长度改变量。此外，材料力学还将剪应变γ 定义为构件上任意两个成直角的微段，在变形过程中角度的改变量，如原来是直角减小了α，则剪应变（也称为切应变）被定义为

并且定义当角度减小时，剪应变为正；而当角度增大时，剪应变为负。弹性力学中更强调每一点处的应变，选择任意点P，以P 点为基准，在x、y、z 方向上分别取微段△x=PA，△y=PB，△z=PC，如图6所示，该点处的变形可由该点处三个方向的线段变形εx、εy、εz 以及三个剪应变γxy、γyz、γzx 共6个应变分量。线应变分别表示微线段PA、PB 和PC 趋近于0时，它们各自的改变量△l 与原长△x 的比值，以εx为例，表示为

剪应变分别表示∠APB、∠BPC、∠APC 在变形过程中的减小量，规定角度增加则表示剪应变为负。

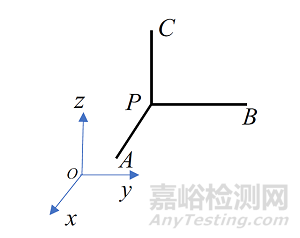
图6

3. 材料力学里讲到构件位移时，主要介绍杆件拉伸作用下截面的伸长、压缩位移，圆杆扭转时截面之间发生的相对转动，以及梁弯曲时截面绕中性轴的转角和挠曲线，这些位移描述都是选取了杆件结构特征几何量，如杆件截面、代表梁中性层的轴线等。

在弹性力学中，结构的变形不再从特定的几何形状上分析，而是直接确定弹性体上每一点的位移。当然，确定了每一点的位移自然可以确定构件上几何特征量的变形特点。因此，在弹性力学中位移指弹性体上每一点的位移，空间一点的位移通常可表示为x、y、z 三个方向上的位移分量，分别用u、v、w 来表示，共三个位移分量。如果只研究平面问题，只需要考虑x、y 两个方向的位移u 和v。

4. 材料力学中的外力一般被区分为集中力、分布力，是按照载荷的分布形式来区分的。在弹性力学中，外力被分为面力和体力两种，这是按照载荷的作用位置加以区分的。当外力作用在物体表面时，则称之为面力，如手推动物体时的推力以及放置在桌面上物体受到桌面的支撑力等。需要注意的是，弹性力学中面力也强调每一点处所受到的力，定义面力时，先在物体表面任选一点，以该点为基准取一个微面△S，设该微面上所受的力为△F，面力用图片表示，其定义为

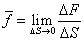
上述定义的面力为任意方向，可向坐标方向投影后，其分量标记为图片、图片、图片。由上式可以看出，面力的定义十分类似于应力，只是应力是物体内部相互之间的作用，面力是物体表面其它物体对它所施加的作用。还应注意，力的单位是N，从上式可以看出，面力的单位为N/㎡，所以，面力并不是力，而是力在某一点的分布集度。这是一个更一般化的定义，它表明面力作用都是分布力，集中力实际上是不存在的，只是力的作用面积远小于物体表面时的一种近似。

当外力可以作用物体上任意一点，无论该点是物体内部的点还是物体表面的点，这样的外力被称为体力，常见的体力如重力、由加速度产生的惯性力、电磁力等。定义体力时，先在物体上任选一点，以该点为基准选取一微小体积△V，设该微小体积上所受的力为△F，将体力用f 表示，其定义为

可见，体力也不是力，它的单位是N/m³，体力乘以体积后才是力。

再次，弹性力学中，对于剪应力的正负规定不同于材料力学。材料力学中，剪应力规定使微元体顺时针旋转的剪应力为正，而将使微元体发生逆时针旋转的剪应力规定为负，如图7所示。

图7

弹性力学希望构建一套只依赖于坐标，而不依赖于具体观察者位置的理论体系。为了说明弹性力学中应力分量的符号规定，画出如图8所示的六面体微元，做如下规定：

考察六面体六个微面，定义外法线方向与坐标轴正向一致的微面为正坐标面，外法线方向与坐标轴正向相反的微面为负坐标面；

无论正应力还是剪应力，做如下统一规定：在正坐标面上，若应力分量与坐标轴正方向一致为正，否则为负；负坐标面上，应力分量与坐标轴正向相反为正，否则为负。

如图8，实线所示的应力分量均在正坐标面上，因此它们的正方向都与坐标正方向一致；而虚线所示的应力分量均在负坐标面上，因此它们的正方向都与坐标正方向相反。在弹性力学中，应力分量的方向始终为正方向。这样，在求得的应力为正时，说明真实应力方向与画出的方向一致；当求得的应力为负时，说明真实应力方向与画出的方向相反。根据定义，弹性力学中正应力与材料力学中正应力方向相同，依然是拉应力为正，压应力为负；但剪应力则与材料力学中的相反。

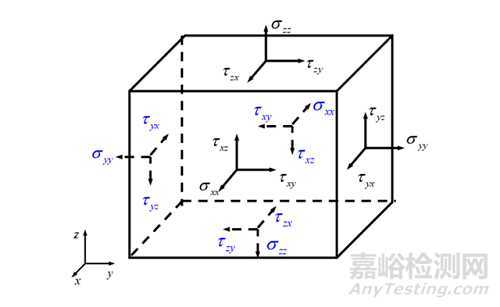
图8

应力分量的下标按照如下规则标记：第一个下标为该应力分量所在的微面外法线方向，第二个下标为应力分量的作用方向。如σzz，表示其所在平面外法线与z 轴平行，同时该应力方向也与z 轴平行。如τzx，则表示其所在平面外法线与z 轴平行，应力方向与x 轴平行，如果是τzx，则恰好相反。在多数情况下，当两个下标相同时，只写出一个，如σ 也是σzz。

此外，在材料力学中存在着许多从实验现象总结出来的经验结论，由于缺乏严格的证明，这些结论最多只能称为“假说”。如平面假设，认为梁在发生弯曲时，梁的每个截面只绕其中性轴发生一定角度的旋转，而平面内的点没有垂直于该平面的位移，在弹性力学中，可以从数学角度严格证明平面假设成立的前提条件。再例如，材料力学提到结构中开圆孔时，会引起应力集中，我们也将在弹性力学中看到，这样的应力集中可以利用数学进行精确求解，并给出应力集中的程度。

当然，弹性力学也继承了材料力学的工程目标，即确保工程结构的强度、刚度、稳定性。在材料力学中，强度问题主要通过细长结构中的应力、应变来分析，刚度问题主要通过变形来分析，稳定性问题主要关心压杆失稳的临界载荷。相对应的，弹性力学借助于微元体，可以求出弹性体任意点的应力、应变和位移，那么，这些解对应于材料力学的工程目标，应力、应变解可用于分析弹性体的强度问题，应变和位移可以分析弹性体的刚度问题，应力可以分析弹性体的稳定性问题，也就是说弹性力学与材料力学具有相同的工程目标。

参考文献：

Mechanics of solids - Continuum plasticitytheory | Britannica.

https://www.britannica.com/science/mechanics-of-solids/Continuum-plasticity-theory

徐芝纶. 弹性力学（第5版）.高等教育出版社. 2016.3

马宏伟,张伟伟. 工程力学十讲. 高等教育出版社.220.9