一、引言

随着《中国制造2025》的推进，智能制造蓬勃发展，工业制造的精度和质量控制也将更加严格。为了维持工业制造的生产水平，很多企业都建立了内部或第三方实验室来实现质量把控。而实验室的质量把控在很大程度上取决于用以进行检测或校准的仪器设备的量值溯源，即采用准确可靠的计量器具对被测量进行测量。因此，研究适用于智能制造的测量不确定度新型评定方法并做好测量结果的测量不确定度评定，对于提升制造业中的生产质量水平和检测水平具有极大的推动作用，对于支撑国民经济高质量发展也具有重要意义。

二、GUM法和蒙特卡洛法的现状及问题

依据目前的计量技术规范JJF1059，通用的测量不确定度评定方法有两种，GUM法和蒙特卡洛法(MCM)。GUM法是一种应用测量不确定度传播律的方法，该方法是国际组织ISO/IEC在GUIDE98-3:2008《测量不确定度表示 第3部分 测量不确定度表示指南》中推荐采用的。在采用GUM法进行测量不确定度评定的流程中有一个关键步骤，就是要建立测量模型。测量模型的建立是基于测量方法，考虑不确定度对被测量的影响而定的，反映了测量结果与其直接测量的量、引用的量以及影响量等有关量之间的数学关系。GUM法主要适用于测量模型为线性函数的情形，当测量模型为非线性的函数时，需要采用泰勒级数展开并忽略高阶项，将被测量近似为输入量的线性函数。正是由于GUM法的适用范围受限，不能处理明显呈非线性的测量模型，其替代方法MCM产生。MCM是利用概率分布的随机抽样而进行不确定度传播的方法，主要适用于各不确定度分量大小不相近、测量模型明显呈非线性以及输出量的概率密度函数明显非对称等情况。对于物理量测量，测量模型一般根据物理原理确定。而对于非物理量或不能用物理原理确定的情况，一般由实验方法确定或给出数值方程。在可能情况下，尽可能地由经验模型给出。某些情况下，输出量的每个输入量可以看作被测量，也可能取决于其他量，从而导出十分复杂的函数关系。在测量不确定度评定中，GUM法和MCM主要是对测量模型能够显式表达的系统进行评定。

然而，随着现代信息技术的发展，人工智能技术与制造业深度融合，在产品的校准检测环节，测量不确定度评定所需建立的测量模型更为复杂。究其原因，主要在于有些现有计量器具自身的系统比较复杂，采用新技术之后的计量器具测量原理变得不清楚，或者利用新技术制造的新的测量装置系统原理模糊等。相关的计量器具主要应用在动态视频和静态图像识别、人脸识别、模式识别等领域，如生产线质量缺陷检测、机械臂自动定位抓取零部件、无人驾驶汽车视觉感知系统、智能汽车动力系统、高速测速拍照系统等。系统变得更为复杂的结果就使得测量模型无法由物理原理或经验方程给出，更不能由函数公式显式表达，因而传统的测量不确定度评定方法就不适用了。

三、深度学习

深度学习是机器学习研究中的一个新领域，在处理大数据方面很有优势。在复杂系统模型未知的情况下，深度学习可以运用算法从原始数据中提取信息，将系统用某种类型的模型表示，并使用该模型对其他数据进行推断，这是深度学习算法最主要的特点。近年来，深度学习的发展逐渐成熟，很多复杂函数都可以通过运用深度学习算法表示。而且深度学习已经广泛应用在语音识别、图像识别、人脸识别、自然语言处理等领域，同时也出现在了现代制造业的众多生产检测环节中。

因此在测量系统的理论模型不清楚或测量系统过于复杂而无法建立测量模型的情况下，采用深度学习算法来拟合复杂系统，建立测量模型是可行的。

四、测量不确定度的深度学习评定方法

测量不确定度的深度学习评定方法分为数据收集、深度学习模型训练、模型不确定度评定、蒙特卡洛方法模拟等步骤。

1.数据收集

针对特定的复杂系统，尽可能多地收集与被测量相关的数据，形成数据集。例如针对智能汽车障碍物识别系统，收集不同温度、湿度、气候、路况、电磁场、光照、速度和障碍物等相关参数，形成数据集；或者针对人脸识别系统，收集不同背景、光照、面部、头部装饰物下的人脸数据，形成数据集。

2.深度学习模型与测量模型的关系

目前有PaddlePaddle、Tensorflow、Caffe、Theano、MXNet、Torch和PyTorch等多种深度学习框架工具，用于快速构建深度学习程序。在这些框架下有许多深度学习模型，如卷积神经网络(Convolutional Neural Network， CNNs)、深度置信网络(Deep Belief Network， DBNs)和堆栈自编码网络(Stacked Auto-Encoder Network， SAE)模型等。

深度学习算法，其基本原理是通过输入层的大数据和输出层对应结果，训练构建一个复杂的参数隐层，从而形成一个深度学习模型实例。在使用时，当有未知结果的一组输入层数据输入该深度学习模型实例后，依据模型实例隐层参数就可以计算出对应的结果，如图1所示。

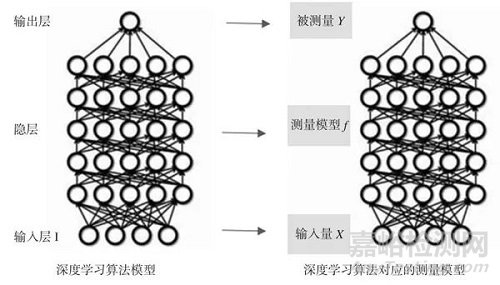
图1  深度学习算法模型与测量模型的关系

从测量模型而言，深度学习模型的输入层I就对应着测量模型的输入量X；深度学习模型的隐层就对应着测量模型f；深度学习模型的输出层就对应着测量模型的被测量Y，如图1所示。

在测量上可以理解为当测量模型f未知时，如何对被测量Y进行测量不确定度评定。

3.测量模型f的求取，即深度学习模型实例的训练

对于不同的复杂系统，比如汽车动力系统、图像识别系统和模式识别系统等，用同一种深度学习算法模拟可能会产生截然不同的效果，选取不同的激活函数、不同的神经网络层数、每层不同的神经元个数或参数个数，都会对测量产生不同的影响。因此在进行深度学习训练时，依据如下过程开展:

(1)将收集到的数据分为训练集T和验证集V。

(2)从PaddlePaddle、Tensorflow、Caffe、Theano、MXNet、Torch和PyTorch等工具中选定深度学习框架。

(3)选定深度学习模型，如从CNNs、DBNs或SAE等模型中选取一个进行编程。

 (4)使用训练集T进行训练，并获得模型实例。

(5)使用验证集V验证模型实例。

(6)获得深度学习模型实例f及估算其可能影响的概率分布DMPF(分布的相关特征值和概率由深度学习工具提供或估算)。

该深度学习模型实例即隐式的测量模型f，并且工具给出的模型实例的概率分布就是该测量模型的测量不确定度的概率分布。

4.利用已有的蒙特卡洛方法进行被测量Y的测量不确定度评定

对于已知输入量X的测量，要求得被测量Y，并求其相应的测量不确定度。由于测量模型f的隐式特性，因而需要采用蒙特卡洛方法进行。其方法如下:

(1)对输入量X中的每个分量xi(i=1，2，……，n)，求其相应测量数据的均值，并使用B类方法和A类方法评定其标准合成测量不确定度。

(2)使用蒙特卡洛方法依据输入量每个分量xi(i=1， 2，……，n)的概率分布和标准合成测量不确定度，生成对应的随机数xij， i=1， 2，……， n；j=1，2，……， m。

(3)对于1≤k≤m，如取j=k，从xij中抽取x1k，x2k，……， xnk，形成一组输入量数据(x1k，x2k，……， xnk)，将该组数据输入深度学习模型实例f，获得一个待测量值yk，并且可由深度学习模型实例计算出yk的概率分布DMPFk，直到生成m个yk和对应的概率分布DMPFk。

(4)按1……k……m的顺序,依据yk和其对应的概率分布DMPFk，使用蒙特卡洛方法生成l个ykp(p=1，2，……， l)，共生成m×l个Y的模拟值。

(5)求取m×l个ykp(k=1，2，……， m；p=1，2，……， l)的均值作为被测量Y的估计值，其分布作为被测量Y的分布，其标准差作为被测量Y的标准测量不确定度。

上述过程，即为测量不确定度的深度学习评定方法，其流程如图2所示。

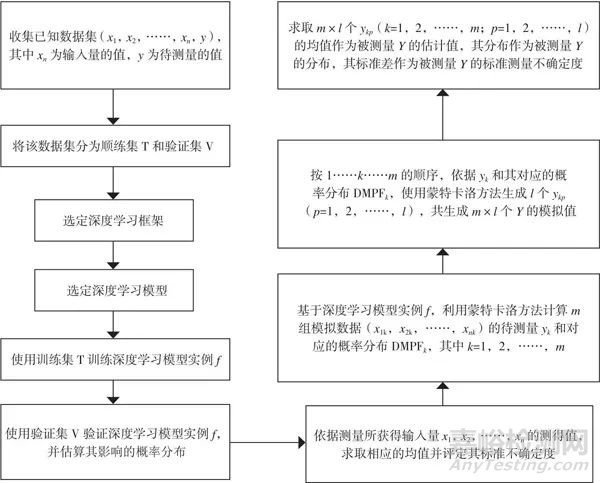
图2  测量不确定度的深度学习评定方法

五、结束语

本文从理论上提出了一种对于不可显式表达的复杂测量的测量不确定度评定方法，对智能制造、人工智能等技术的质量提升具有显著意义。