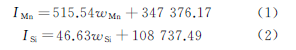电子探针显微分析仪(EPMA)在金属行业中应用广泛,一般使用ZAF理论修正模型进行微区定量计算。ZAF理论修正模型由原子序数效应(Z,包括背散射效应和基体阻碍能两部分)、吸收效应(A)和荧光效应(F)构成。对于低含量元素,特别是在基体中主量元素可能会对低含量元素产生严重干扰的情况下,ZAF理论修正模型中的修正量会很大,导致定量分析的误差变大。因此,可以使用校准曲线法对钢中低含量合金元素进行定量计算。校准曲线法采用一系列元素含量呈梯度变化的标准试样,建立了元素含量和特征X射线计数强度之间的对应关系曲线,该曲线可用于基体效应与标准试样相同或类似的待测试样定量转换。
在GB/T 17360—2020 《微束分析 钢中低含量硅、锰的电子探针定量分析方法》中给出了低含量元素的测试方法,但其中存在一些待商榷的技术细节,如在用测试低含量Mn,Si元素相同的测试条件测试纯物质标准试样的Mn,Si元素含量时,计数器存在饱和及死时间问题,且引入计数强度比参与计算会带来更多的传递误差。针对上述问题,依据GB/T 15247—2008 《微束分析 电子探针显微分析测定钢中碳含量的校正曲线法》,来自岛津企业管理(中国)有限公司的赵同新、崔会杰等研究人员结合了GB/T 17360—2020,GB/T 15247—2008 两个标准的优点,给出了钢中低含量合金元素定量测试和不确定度计算的可行方法。
1、测试方法
取一套基体类似、各元素含量不同的低合金钢标准试样5个,用于建立校准曲线。待测试样经导电树脂热镶嵌后,使用不同粒度砂纸对表面进行机械磨制,然后分别使用3,6,9μm等粒径的金刚石悬浮抛光剂进行抛光处理。
2、校准曲线的建立
使用低合金钢标准试样建立校准曲线,标准试样中Mn元素的质量分数分别为0.660%,1.040%,1.500%,0.255%,0.006%,Si元素的质量分数分别为0.233%,0.390%,0.740%,0.067%,0.008%。在每个标准试样上随机选择10个无污染的区域,采集Mn,Si元素的特征X射线计数强度,测量结果分别如表1,2所示,去掉最大值和最小值后,取平均值建立校准曲线(见图1)。



从图1可以看出,Mn,Si元素的质量分数和特征X射线计数强度具有很好的线性关系。根据GB/T 15247—2008附录A,计算可得Mn,Si元素的质量分数(w)和特征X射线计数强度(I)的关系分别如式(1),(2)所示。
3 定量测试结果及不确定度计算
3.1 定量测试结果
在待测试样上随机选择3个点,分别测量Mn,Si元素的特征X射线计数强度,结果如表3所示。将Mn,Si元素的特征X射线计数强度平均值分别代入式(1)和(2),可以得到Mn和Si元素的质量分数分别为0.12%和1.36%。
3.2 不确定度
将表1,2中的数据代入GB/T 15247—2008附录A中的不确定度计算公式,得到待测试样中不确定度计算的相关数值如表4所示。由表4中的相关数值计算可得,待测试样中Mn元素的测量不确定度为0.0024%,Si元素的测量不确定度为0.021%。
3.3 重复性
使用同一台仪器,在同样的测试条件和方法下,对待测试样进行5组测试,每组3个测试点,Mn和Si元素质量分数的测试结果分别如表5,6所示。
将表5,6中的数据代入JJF 1059.1—2012 《测量不确定度评定与表示》中的计算公式可得:Mn元素5组测试值合并样本的标准偏差为0.00228,重复性相对标准不确定度为0.00059;Si元素5组测试值合并样本的标准偏差为0.00693,重复性相对标准不确定度为0.0018。
3.4 扩展不确定度
取包含因子k=2时,Mn元素的扩展不确定度为0.0048%,Si元素的扩展不确定度为0.042%。
在建立校准曲线的标准试样中,Mn元素的质量分数为0.006% ~1.5%,Si元素的质量分数为0.008%~0.74%。在待测试样中,Mn元素的质量分数为0.12%,Si元素的质量分数为1.36%,其中待测试样中Si元素的质量分数超出了标准试样中Si元素的质量分数,这也是导致Si元素的扩展不确定度略大一些的原因。
4、结论
对于低合金钢中低合金元素的电子探针微区定量测试,使用标准试样建立校准曲线法是一种很好的定量分析方法。各低含量合金元素在测试条件合适的情况下,元素的质量分数和特征X射线计数强度具有很好的线性关系。
使用校准曲线法对待测试样进行定量测试和测量不确定度的计算,低含量元素的定量结果也有很好的稳定性和重现性。取包含因子k=2时,待测试样中Mn元素的质量分数为0.12%,扩展不确定度为0.0048%;Si元素的质量分数为1.36%,扩展不确定度为0.042%。