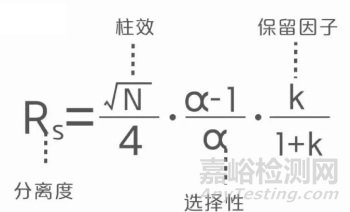
色谱理论中,分离度Rs公式有多种表达形式,然而笔者认为,包含塔板数N,保留因子K,选择性α的表达式最具实践指导意义。
图1分离度Rs表达公式
如图1所示,此公式清晰体现了分离度Rs与塔板数N,保留因子K及选择性α之间的数学关系。如何利用此公式指导具体的方开发,达到理想的分离效果呢?笔者对此进行简单解读。
塔板数N的应用
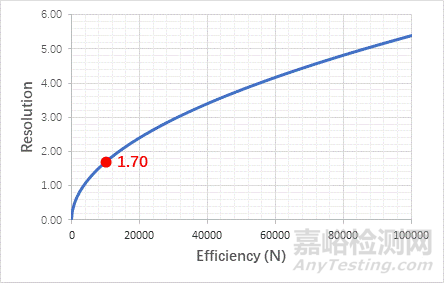
图2:分离度Rs与塔板数N之间的关系
分离度Rs与塔板数N之间的关系如图2所示。由图可知,分离度Rs与塔板数N在一定区域内近似接近线性关系,随着塔板数N的增加,分离度Rs会一直增加。正是源于此关系,所以寻找高效的色谱柱成为广大色谱工作者改善分离的常用手段。
如何挑选高效的色谱柱,我们首先要了解如何估算色谱柱的柱效。
色谱柱柱效估算公式如下所示:
N≈500L/dp
L—色谱柱长度(mm),dp—颗粒直径(um)
由上述公式可知,柱效N与柱长L成正比,与粒径dp成反比。因此,只要我们在原来色谱柱基础上增加柱长、减小粒径或者同时采取这两方面的措施,均能做到增加柱效。至于增加的比例,则由上述公式可计算。另外,上述公式简化为L/dp后则可用于以比较两根色谱柱是否等效。例如两款色谱柱,分别为4.6*150mm,3um和4.6*250mm,5um,由公式L/dp可推知,两者L/dp=50,因此两款色谱柱可视为等效。目前市面上除了常规全多孔外颗粒色谱柱外,核壳颗粒色谱柱也越来越受到重视,其中一方面就是其出色的柱效。与传统全多孔颗粒色谱柱比较,其柱效往往提高20%以上。
根据图1分所揭示的数学关系,我们可利用此公式预判改变柱效N后获得的分离度Rs。例如,某物质在4.6*250mm,5um的色谱柱上的分离度为1.0,尝试更换为同款4.6*250mm,3um的色谱柱。由公式推算可知,更换后其达到的分离度约为1.3。因此,利用此公式通过对分离度的预判,可避免不必要的试验。
保留因子K的应用
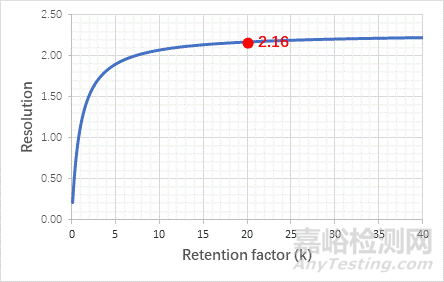
图3分离度Rs与保留因子K之间的关系
分离度Rs与保留因子K之间的关系如图3所示。在讨论分离度Rs与保留因子K之间的关系前,笔者先介绍一下保留因子K的计算公式,如下所示:
K=(tR-t0)/ t0,
t0—死时间,tR—溶质保留时间
由图3可知,当保留因子K≤5时,通过改变K值,分离度都能得到极大的改善。当保留因子K≥10,通过改变K值,分离度得到的改善却极小。因此,方法开发过程中,如果色谱峰的保留因子K≤5,此时通过改变K值便能有效的改善分离。如果色谱峰的保留因子K≥10,此时通过改变保留因子K将会收效甚微。因此当保留因子K≥10时,改变其他参数将会更加有效。
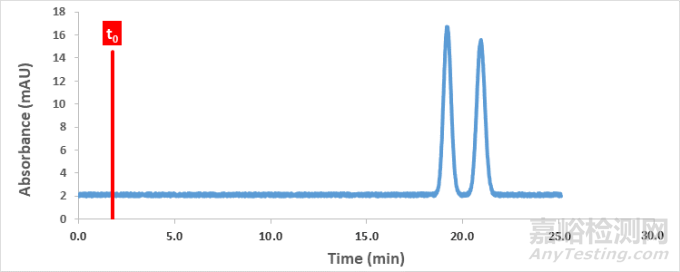
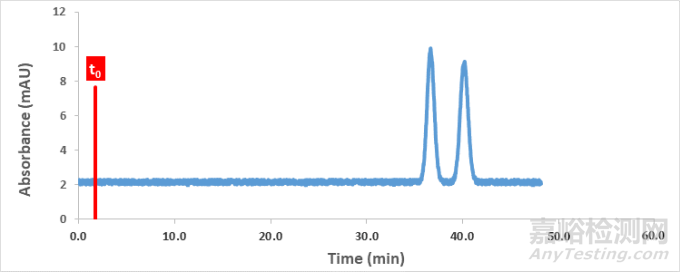
如图4案例所示,当K=10时,二者的分离度为2.07;当K=20时,二者的分离度仅为2.16。虽然二者分离度略有增加,但此时付出的代价却是检测时间的加倍。因此,当K≥10时,利用K值改善分离度并不是一种明智的举措。
图4分离案例:K=10(上图)与K=20(下图)分离图谱
选择性α的应用
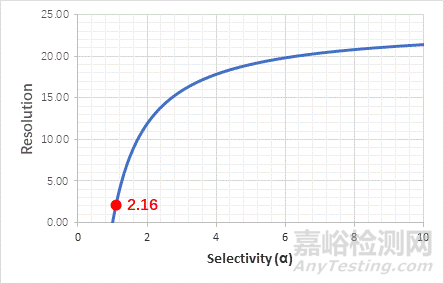
图5分离度Rs与选择性α之间的关系
分离度Rs与选择性α之间的关系如图5所示。而选择性α的计算公式如下所示:
α=k2/k1
k1—色谱峰1的保留因子,k2—相邻色谱峰2的保留因子
由图可知,当选择性1≤α≤2时,通过改变α值,分离度都能得到极大的改善。当选择性α≥6时,通过改变α值,分离度Rs得到的改善相对变小。比较图2、图3及图5纵坐标分离度Rs数值可知,影响分离的三要素中,选择性α对分离的影响是最大的。即使选择性α的微小改变,也能带来分离度Rs的巨大改变。所以,选择性α是改善分离度Rs的最有效方法。
实际工作中,对于选择性α我们所用到的区域一般都是1≤α≤2的区域。为什么应用仅仅在此区域内呢?笔者用以下案例为大家解读。色谱分离中,一般保证溶质的K介于1≤K≤10区间内。假设某物质分离条件为4.6*250mm,5um的色谱柱,流速为1.0ml/min,此时t0≈2.5min。当某物质保留因子K1=1,若α=2,则相邻物质K2=2,此时两物质的保留时间分别为t1≈5.0min, t2≈7.5min,这种情况下,二者已经完全分离。因此选择性α>2时,分离度Rs已经满足要求,不必再改善分离。所以,选择性α在1≤α≤2的区域才有改善的必要。
分离条件对三要素的影响
以上部分,我们对分离度Rs与塔板数N,保留因子K,选择性α之间的关系进行了论述。那么方法开发过程中,如何改善这三要素呢?通过图6我们可以找到具体的控制措施。
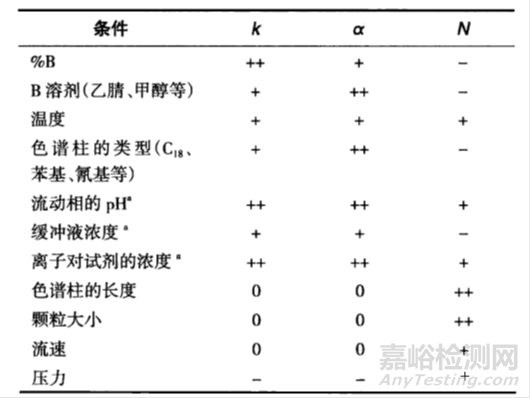
图6分离条件对塔板数N,保留因子K,选择性α的影响
++—主要影响,+—次要影响,-—相对影响较小,0—没有影响,a— 对于可电离的溶质分子来说。
由图6可知,塔板数N受影响条件较多,其中色谱柱长度和颗粒大小是影响塔板数N的主要条件,其具体计算公式前文也已经有论述,其他条件对塔板数N的影响相对较小。保留因子K主要影响因素包括有机相比例B%,流动相pH以及离子对试剂浓度。对于不可电离的物质而言,流动相pH以及离子对试剂浓度对保留因子K就不再是主要影响因素。选择性α的主要影响因素为溶剂种类、色谱柱类型、流动相pH以及离子对试剂浓度,其他条件影响相对略小。当然有些分离条件对三要素的影响并不是孤立的,比如流动相pH,在改变保留因子K的同时也改变了选择性α。因此,当我们明白分离条件对塔板数N,保留因子K,选择性α的影响大小之后,后期开展工作才会有的放矢,更加高效。
以上便是笔者对分离度Rs与塔板数N,保留因子K,选择性α之间的关系进行的解读,鉴于笔者能力有限,若有不当之处,敬请各位读者指正。