1.1.1 概率密度函数
概率密度函数(Probability Density Function),指整个时间范围内的失效分布,和反映了产品完全失效的速度。记为f(t)。f(t)的值越大,说明在时间周围的很小区间内发生的产品失效越多。尽管f(t)很少被用来量化可靠性,但是它是获得可靠性指标的重要基础。
1.1.2 可靠性函数
可靠性(Reliability)是指产品在规定的条件下、规定的时间内完成规定的功能的概率,记为R(t)。可用下式表达,见公式:
以LED照明产品为例来解释这个三个规定:
1) “规定的条件”:这个条件包含应力类型、量级、使用率、运行剖面等。LED产品应用中,温度、湿度、电压、振动,腐蚀等都是比较常见的应力条件。比如室内照明一般规定温度范围为-20~35度,湿度范围为30%RH~60%RH,户外照明一般规定温度范围为-40~65度,湿度范围为10%RH~85%RH。家用照明每天开关次数平均3~4次,而商业照明为1~2次。
2) “规定的时间”:这个时间可以是保修期、设计寿命、任务周期等等。这个规定的时间必须能体现客户的期望,并且具备市场竞争力。如某知名LED企业宣称他们的一款LED射灯的寿命时间为25000小时。而在时间到达25000小时后,可靠性要求为50%。
3) “规定的功能”:LED灯泡能正常发出光亮,并且光输出在初始值的70%以上,颜色没有发生漂移,那么这个就是规定的功能。
1.1.3 失效分布函数
失效分布函数又称累积失效分布函数(Cumulative Distribution Function),指产品在规定的条件和规定的时间内发生实效的概率,记为F(t)。可用下式表示,见公式:
众所周知,R(t)与F(t)是一对互补的函数,即R(t)+F(t)=1。因为在开始工作时, 没有任何产品出现问题,即R(0)=1,F(0)=0。随着时间的增加,失效数也不断增加,可靠性也相应减小。下图反应了R(t)与F(t)随时间的曲线变化:
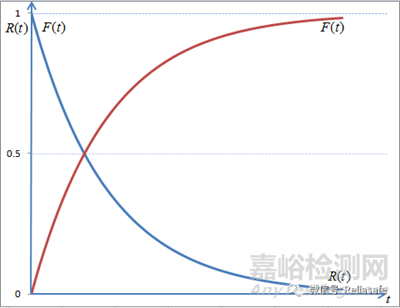
可靠性与累积失效关系
1.1.4 失效率函数
失效率是指已工作到t时刻的产品,在时刻t后单位时间内发生失效的概率,记为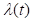 。公式表示为:
。公式表示为:
虽然f(t)也能反映产品失效的变化速度,但是与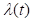 相比却显得不够灵敏。通常,根据失效率在时间轴上的变化趋势,可以分为三种不同的类型:递减型、恒定型和递增型。按失效率变化规律,可把产品的全部寿命周期分为三个时期,如下图所示:
相比却显得不够灵敏。通常,根据失效率在时间轴上的变化趋势,可以分为三种不同的类型:递减型、恒定型和递增型。按失效率变化规律,可把产品的全部寿命周期分为三个时期,如下图所示:
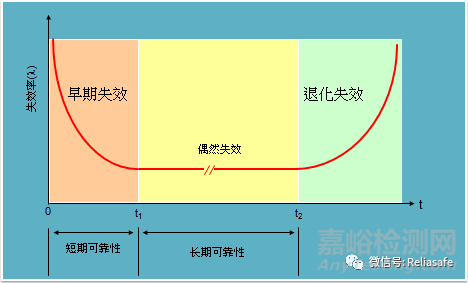
浴盆曲线
1) 早期失效:这里一阶段的失效由于元器件来料缺陷、工艺制程异常、客户误操作等原因引起。随着时间的推移,失效率成递减趋势。跟其他电子行业类似,LED照明企业也通过老化,应力筛选等方式来剔除不良品,瞬时失效率得以下降,而留存下来的产品就更加可靠了。
2) 偶然失效:这一时期的产品失效率近似恒定不变,产品主要由于过应力超过设计强度而所导致的失效。例如:由于意外或瞬时的电路过载引起LED损坏,或者应用环境突然恶化导致LED照明系统温度过热,造成元器件损坏。对于这一阶段的失效,可以通过降额设计、容差分析、HALT等方法来提高产品的安全欲度,从而获得更低的失效率。
3) 退化失效:产品的材料、元器件,焊点,连接器等,由于性能衰退、疲劳累积、磨损等原因,出现失效率递增的现象。为了降低失效的影响,可以通过预防性维护、定期更换等方式来实现。对于LED照明这样的不可维修的产品,只能通过优化设计,改进工艺流程,选取优质元器件来延长有效使用周期,从而淡化退化失效的影响。

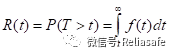
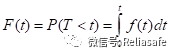

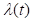 。公式表示为:
。公式表示为: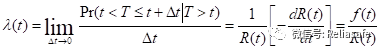
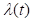 相比却显得不够灵敏。通常,根据失效率在时间轴上的变化趋势,可以分为三种不同的类型:递减型、恒定型和递增型。按失效率变化规律,可把产品的全部寿命周期分为三个时期,如下图所示:
相比却显得不够灵敏。通常,根据失效率在时间轴上的变化趋势,可以分为三种不同的类型:递减型、恒定型和递增型。按失效率变化规律,可把产品的全部寿命周期分为三个时期,如下图所示:



