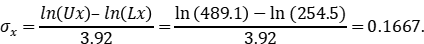在工程设计/开发中，一个常见的问题是如何确定设计已经实现了真正的改进，以便我们判断是否仍然需要改进某些设计特征参数。
例如，在开发的早期，工程师只有约8个部件来执行可靠性测试。很快，可靠性测试产生了失效，工程师得出了可靠性水平太低的结论。在设计变更后，工程师再次进行了相同的可靠性测试，假设这次有10个部件，失效时间似乎比上一代设计更长，那么工程师该如何知道所观察到的改进是真正的改进，而不是偶然的测试结果?
为了帮助工程师，我们可以采用在可靠性工程中的一种方法，就是比较两种设计的B10寿命，以查看设计2 (D2)是否优于设计1 (D1)。D2可能只是D1做了些修改，D2也可能是采用与D1完全不同的技术，当然这个前提是部件的使用寿命能够满足性能的要求。请注意，B10寿命是指10%的总体(population) 失效时所对应的寿命(例如，工作小时数或周期)，也就是说，90%的总体会存活超过B10寿命， 或者说可靠性在B10寿命时为90%。
本文将讨论使用B10寿命的近似方法来比较两种设计。我们将用一个示例来说明该方法的步骤。
图1有两条威布尔(Weibull) 曲线(每条都有90%的双侧置信曲线)，显示了两个设计D1和D2的失效分布。
图1
图1由随机数据生成(我们使用eWeibull)，其中:
设计1 (D1)的β（形状参数, shape parameter） = 2, η
（尺度参数, scale parameter）= 900小时。
设计2 (D2)的β =3.5, η =1300小时。
两组的样本量均为n = 30。
我们需要一个“验收标准”来确定结果是否足够好，而不是由偶然因素所造成的。我们可以将验收标准设定为:“在最小为90%的置信度下，D2设计的B10寿命比D1设计的B10寿命更长/更好。”
但是请注意，当我们做样本测试时，我们得到的都是样本统计量。样本统计存在抽样误差
(sampling error)，图1的拟合曲线两侧的边线就是威布尔拟合分布90%的置信区间。如果你想估计某一时间的可靠性，那么对于这个可靠性的变异（或者说置信区间分布）是显现在y轴上的。同样，如果你想要在某个累积失效概率上估计一个百分位数
(percentile)，那么这个百分位数的变异（或者说置信区间分布）是显现在x轴上的。
图2显示了一条红色的标记线，代表y轴上的10%（也就是10% 的累积失效概率）。我们可以看到D1设计的B10寿命置信区间分布(红色)和D2设计的B10寿命置信区间分布(蓝色)。
图2
在图2的示例中，我们有以下来自eWeibull软件的估计值(这些是极大似然方法估计值(MLE))。具体含义见图3。
D1设计(我们用X来表示):
β = 2.579
η= 844.24小时
B10,x = 352.8小时(这是x或D1设计的B10寿命)
Lx为B10,x的置信下限， = 254.5小时
Ux为B10,x的置信上限， = 489.1小时
D2设计(我们用Y来表示):
β = 3.409
η=1324.47小时
B10,y = 684.5小时(这是y或D2设计的B10寿命)
Ly为B10,y的置信下限， = 531.4小时
Uy为B10,y的置信上限， = 881.7小时
图3
这些置信上下限是90%的双侧置信区间。它们可以直接从威布尔图中读取，也可以从eWeibull软件中获得.
B10寿命是一个从样本推算出来的统计值，它的分布其实并不遵循典型的正态分布 (normal distribution)。
为了简化理论的推导，作者进行的模拟研究（simulation study）显示B10寿命趋向于服从对数正态(lognormal)分布。一般来说，对于对数正态分布的随机变量W进行转化(V=ln(W)),，那么该随机变量的对数值V将遵循均值(mean,μ )和标准差(standard deviation,σ )的正态分布。
因此，我们可以用“
”的距离来估计
标准差。在90%双侧置信水平上：
因此
推到出
同理，
混合标准差(pooled standard deviation)为
我们现在可以根据应力-强度干涉理论(stress-strength interference theory)计算z值：
作者的模拟研究显示了三个有趣的结果:
MLE程序所产生的B10,x的均值和B10,y的均值会高估(over-estimate)真实值。在我们为图1生成随机值时，D1和D2的真实B10寿命可以由
中得到，而η和β已在前面的章节中给出。
模拟研究运行了200次，我们用两个ln(B10)寿命的距离除以3.92来估算ln(B10)的标准差。这个ln(B10)的标准差通常会被低估(under-estimate).
当在z公式中的分子估计过高，而分母估计过低的情况下，通过模拟研究，计算得到的z值高估了约7.66%。因此，我们建议将z值调整为“调整后的
z’=z*(1/1.0766)=z*(0.93)。
因为我们计算的z = 3.1428，所以“调整后的z’= 3.1428*0.93 = 2.923。因此，相关的置信水平(可以使用excel表格)用公式进行计算如下：NORM.S.DIST(2.923,TRUE)= 0.998 ~ 99.8%置信度。
我们可得到以下两点结论:
从D1到D2经过设计改进, D2设计的B10寿命比D1设计的B10寿命来的大，而且置信度为99.8%。改进时长的点估计(point estimate)约为331小时（= 684.5 - 352.8)。
如果“验收标准”的要求是“最小为90%的置信度”，那么我们就满足要求了。
如果我们想要的是显示改进的寿命增加值(比如，A)为150小时，我们可以这样做来求置信度:
我们需要将ln(B10)的估计标准差转换回(B10)的标准差。利用对数正态分布的性质，
对于D1设计，我们有
对于D2设计，我们有
混合标准差为
那么我们可以应用以下公式计算z值：
因此置信水平为NORM.S.DIST(1.685,TRUE)= 0.95.4 ~ 95.4%.
本质上，我们是在说:
从D1到D2的设计变化，我们有95.4%的信心认为B10寿命改善后的增加值约150小时。
请注意，我们在这里使用的示例是针对n=30的样本量。通常，由于资源和业务运行的限制，我们的样本量要小得多。为了显示样本量的影响，我们将在样本量为30、20、10、8和6时做了下面的两个表。我们随机为每个样本量生成两组数据(一组用于D1, β=2, η=900，另一组用于D2, β=3.5, η=1300)。然后，我们通过上面所示的步骤来估计以下表中的所有值。
由于样本量的不同，我们可以看到β和η值的抽样变化。我们还可以看到，通常样本量越小，调整后的z值越小，导致置信度越低。
图4显示了样本量n=30和n=20时的视觉对比。我们观察到，当n=20时，两条威布尔置信曲线在10%累积失效概率水平线开始重叠。
在图5中，当样本量下降到10、8或6时，重叠变得更加严重。这是可以解释的，因为样本量越小，置信区间就越宽，尤其是在极低的失效概率情况下。
图4
图5
