您当前的位置:检测资讯 > 科研开发
嘉峪检测网 2024-06-06 16:10
一、冷却曲线试验
淬火介质的基本功能是控制淬火过程中零件向淬火介质传热的速率,得到想要的显微组织和力学性能,包括硬度、抗拉强度和疲劳强度,韧性等。同时,淬火过程应控制残余应力和产生尽可能小的变形及开裂倾向。随着热处理行业竞争的加剧,对淬火过程的监控变得越发重要。一致性检查对于确定淬火烈度的变化和验证新的淬火冷却介质和淬火工艺是否合适极其重要。淬火烈度可以通过硬化能力试验来量化,例如横截面硬度检测(U形曲线)或者采用诸如拉什曼试验步骤的末端淬火试验及其他变体试验。然而,这些传统的试验方法都耗时且相对昂贵。另外,冶金反应也随着钢试样化学成分的变化而变化。因此,新的替代试验方案正在被研究,而且将一直值得研究。
除了直接在试样或零件上检测硬度外,还可以通过其他方法来表征淬火冷却介质的性能。一种常用的替代方案是检测淬火冷却介质的冷却能力。虽然人们已经提出多种方案并在继续使用,如热丝试验和GM淬火表试验等,但总体来讲,这些方法是有局限性的,对其数据的解读也要非常小心。从各种试验方案的提出到现在,冷却曲线分析已经被普遍接受,并成为最有用的淬火冷却介质性能检测手段。冷却曲线对影响淬火冷却介质吸热能力的因素很敏感,包括浴温、搅拌、浓度等。
下面将介绍具体方法,包括如何得到冷却曲线、目前采用的标准试验方案以及冷却曲线数据解读新方案的使用(它能更确切地反映淬火过程)。在后者的案例中,将展示各种不同的计算实例。
1. 1 冷却曲线
冷却曲线是冷却过程的时间-温度关系图,包括从热金属表面到较冷的淬火冷却介质之间的界面传热过程。冷却曲线的形状代表了奥氏体化温度的金属试样在淬火冷却介质中冷却的不同冷却机制。图1所示为将热探头浸入可蒸发淬火冷却介质后的三个阶段,包括全膜沸腾阶段(蒸汽膜冷却阶段或A阶段)、核沸腾阶段(B阶段)和对流冷却阶段(C阶段)。由于时间较短以及采集数据所用的探头相对不够灵敏,这一案例中没有观察到冲击膜沸腾阶段(A'阶段)。如前文所述,每个沸腾阶段的整体冷却机制都很不同。从膜沸腾到核沸腾的转变温度曾被称为莱登弗罗斯特温度,它与淬火金属的初始温度无关,如图2所示。
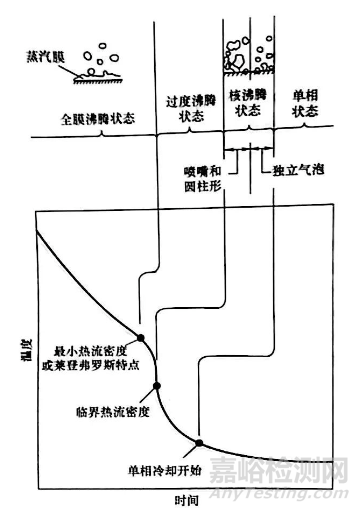
图1 淬入可蒸发介质中的三种冷却机制的冷却曲线

图2 英科(Inconel)镍600探头在水中淬火时冷却速率与时间的关系(虚线代表了莱登弗罗斯特温度)
根据测得的冷却曲线,将冷却速率曲线视作时间或温度的函数来计算是可能的。试样从任一温度冷却下来所需的时间、任一时刻的温度、冷却至任一温度范围所需的时间,都可以很容易地通过计算得到。这些计算通常是由现成的电子数据处理软件完成的,从这一分析中得到初始的 “时间-温度” 数据。图3所示为冷却曲线数据的各种常用表示方法。

图3 各种常见冷却曲线的表示方法
1.2 冷却曲线数据采集
传统上,采用高速记录仪来采集 “时间-温度” 数据。最近,已经使用数据记录器或台式/便携式计算机来采集数据,计算机上带有模拟/数字装置,能将热电偶的模拟信号转换为数字信号以便于处理。对于大多数冷却曲线分析工作,一般数据采集频率为5~20Hz (数据点/s) 。选择该频率范围内的采集数据描绘成平滑、完整的冷却速率曲线(见图4)。多余的数据采集频率将被当成没必要的干扰数据处理掉。
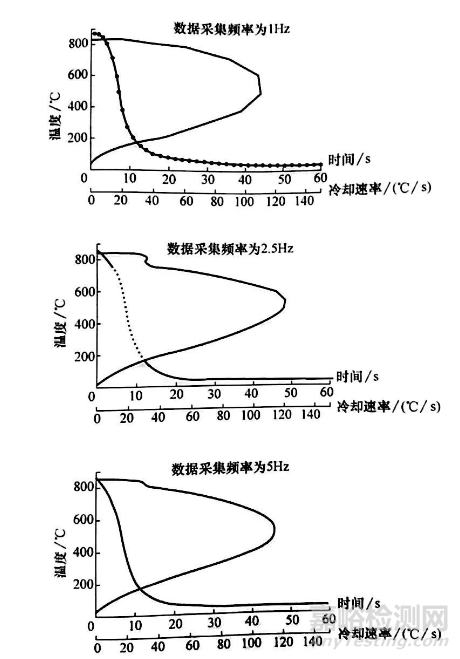
图4 数据采集频率对冷速曲线平滑度的影响
1.3 探头
利用冷却曲线对淬火冷却介质进行冷却行为分析最早是由勒·夏特利埃(Le Chatelier) 在1904年报道的。同年,希戴克(Haedicke) 也做了相关分析。在他们之后,许多种冷却曲线分析(其中大部分包括各种各样的探头尺寸和设计)已经成功地得到应用。勒·夏特利埃采用的是几何中心嵌入一个热电偶的 18mm×18mm (0.7in×0.7in) 的方铁棒。自此之后,人们采用了范围更广的探头形状,包括球形、板材、环状、线圈状、圆盘状及产品零件形状等。探头的制造也采用了各种材料,如合金钢、不锈钢、Inconel 600、银等。目前,标准冷却曲线分析试验中最常用的探头材料是 Inconel 600 和银,304不锈钢则用得较少。合金钢探头实际上并不用于日常的冷却曲线分析,因为由于表面氧化、腐蚀或者开裂,它们不能重复利用。表1列出了室温下各种材料的热导率和热扩散系数的对比,这些数据在计算传热系数时是不可或缺的。
表1 不同材料在室温下的近似热导率和热扩散系数
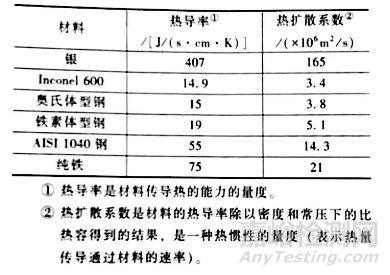
目前,国际上最常用的探头是沃尔夫森(Wolfson) 探头,它是Φ12.5mm×60mm (Φ0.5×2.4in) 的圆柱形Inconel 600探头,其几何中心嵌有一个K型热电偶,如图5所示。
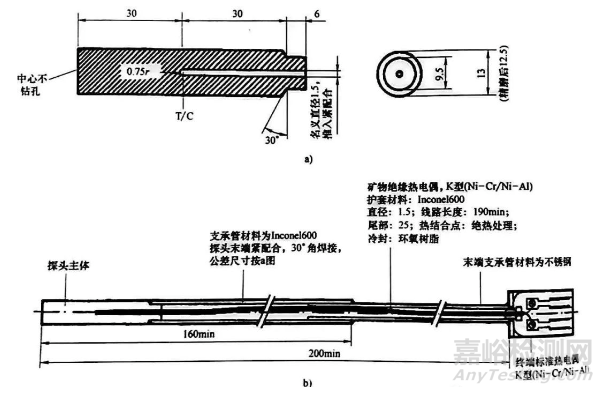
图5 最初报道的用探头进行冷却曲线分析的示意图
这种探头是一些标准的基础,Inconel 600与温度有关的热物理性质见表2。
表2 Inconel 600材料随温度变化的热物理性质
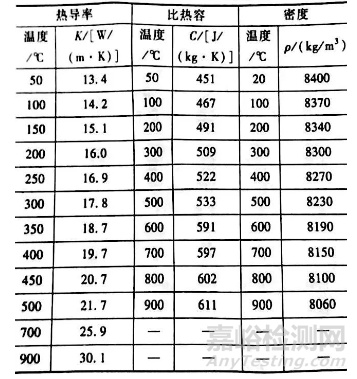
这些国际和国家标准选择 Inconel 600作为探头材料的原因如下:
1) 它的热导率比银更接近于钢。
2) 小的探头尺寸更适用于少量(大约为2L 或者更少)淬火液的质量检测。
3) 淬火过程中铬镍铁合金不发生相变。
4) Inconel 600探头虽然没有银探头对冷却曲线过渡阶段敏感,但是其提供的热电偶信号更为稳定,干扰也更少。但是,有些业内人士还是强烈支持用银作为探头材料。但是近来,其中的表面热电偶设计也被心部热电偶所取代,如图6所示。
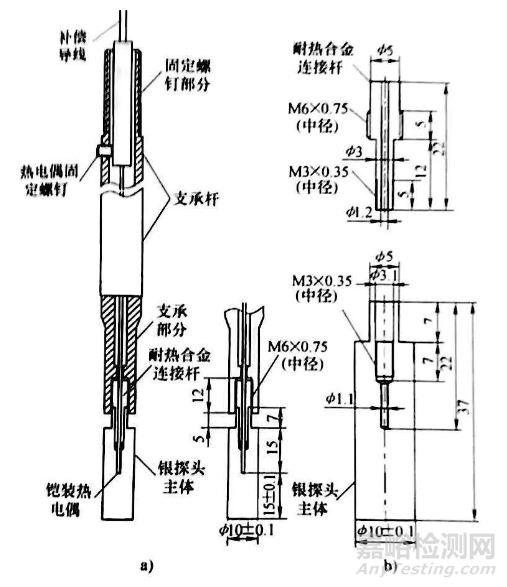
图6 用于ASTM D7646D的银探头示意图
a)总成 b)探头细节(mm)
其他银探头配热电偶时都放在探头的几何中心。在100~1234K温度范围内,与温度相关的银的热导率(W/m·K) 可以用下列多元线性回归方程计算:
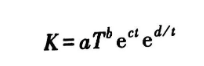
式中,a=230.9532,b=0.113561,c×10E4=-3.19146,d=17.17667,T是温度(K) 。
银的比热容作为温度的函数,可以由相同形式的多元线性回归方程计算,其中a=0.475069, b=-0.35933,c=0.000571,d=-77.0249。据报道,22℃ (72°F) 下金属银的热扩散系数是 1.61cm2/s (0.25in2/s )。酋崎正刚(Narazaki ) 等人以表格形式报道了银的与温度相关的热物理性质见表3 。
表3 酉奇正刚(Narazaki)报道的银的热物理性质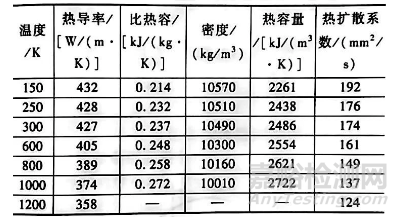
图5所示的尺寸相对较小的 Inconel 600探头及图6所示的银探头遇到的问题之一,是在多个实验室很难得到好的可重复性和再现性。导致这个问题的原因之一,是蒸汽可能在探头浸入底部时被捕获,而不会在探头其他表面已经过渡到核沸腾阶段的同时过渡,特别是在淬入可蒸发淬火冷却介质中时。另一个观察到的潜在难点,是探头底部的锐边也可能造成蒸汽膜破裂时间的不一致,也就是酋崎正刚所说的边缘效应,这在水淬时最为显著。这个问题已经被详细研究过。例如,酋崎正刚等人研究了探头形状对全膜沸腾和过渡沸腾的影响,包括尖端是半球状的和球状的情况。这两种替代平头探头的设计都不会造成与平头探头一样的蒸汽捕获问题。Zhang完成了更广泛的基础研究,他除了确认酋崎正刚所说的边缘对蒸汽膜破裂的影响外,也证实了淬火过程中在平整表面的底部发生的蒸汽捕获问题。吕本(Luebben) 等人和埃尔南德斯·莫拉莱斯(Hernandez-Morales) 等人也证实了这个问题,并且推荐了替代设计,能大体上减轻或消除这一能导致冷却曲线结果不同的问题。此项研究的一部分结果是,弗雷里希(Frerich) 和吕本(Luebben) 推荐采用一种带倒角的探头尖端,以使淬火时探头尖端捕获的气泡最小化。
现在,人们更加注重传热系数和热流密度的计算,以便更好、更全面地表征淬火的全部传热过程。这增加了嵌有近表面热电偶的小探头的使用次数,如图7所示。

图7 Φ13mm×57mm 、锥高10mm的圆柱形304不锈钢探头
注:一个热电偶插入深度40mm处,另一个插入深度50mm处;热电偶孔直径为1.58mm,位于探头表面下2.38mm。

图8 一个Φ25mm×100mm (Φ1.0in×4in)的Cr-Ni钢圆柱体淬入搅拌速度为0.3m/s(1ft/s) 的30℃(85°F) 的水中
由图8可见,当淬入可蒸发液体时,随着钢的冷却,表面的再润湿锋有一个运动过程。沿着探头来定位热电偶,再润湿锋的运动可以通过测定再润湿时间来检测,而再润湿时间可以通过使用多重热电偶探头来测定,它是一个对表征硬度、变形和开裂倾向都很重要的参数。此外,采集到的时间-温度 数据可以用来计算表面传热系数和临界热流密度。最近,一种由腾西设计的 Inconel 600探头(见图9) 被用来计算植物油和矿物油的传热和临界热流密度,并得到了极好的结果。需要注意的是,与矿物油相比,植物油通常很少表现出膜沸腾或者没有膜沸腾。
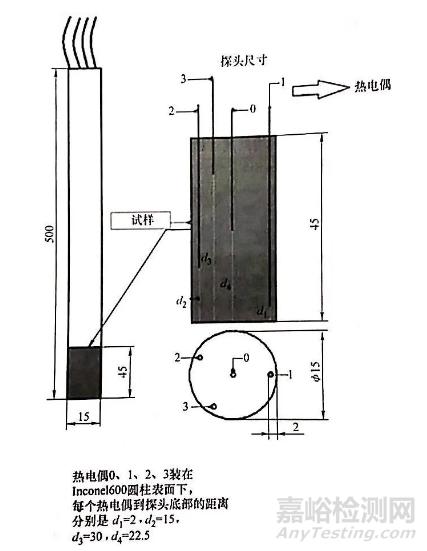
图9 腾西设计的 Inconel 600多电偶探头
虽然淬火时使用近表层热电偶来指示表面温度的重要性得到了越来越多的公认,但在探头尖端设计上并没有达成一致,因为探头尖端的形状能够影响初始表面蒸汽膜的稳定性,为了解决这个问题,埃尔南德斯、莫拉莱索等人就探头尖端设计液流和在探头表面所形成蒸汽膜的稳定性及破裂的一些做了研究,并得出结论,圆锥形的尖端对淬火时液流的扰动最小,图10所示,为对这种最佳探头的说明。
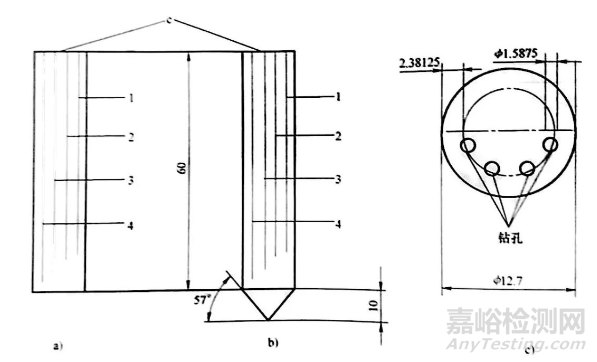
图10 埃尔南德斯·拉莫莱斯等人提出的多电偶圆柱形304不锈钢测试探头
通过对探头表面淬火过程的视频进行分析,吕本等人也注意到了探头尖端平整表面的问题,他们提出了一种具有倒角尖端的探头设计,如图11所示。
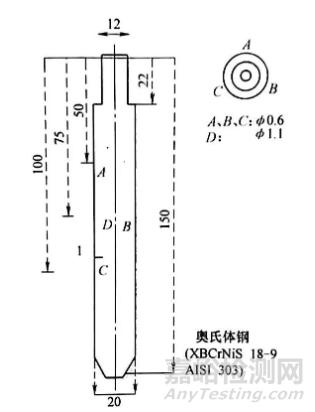
图11 吕本等人提出的303型奥氏体型不锈钢探头(尖端倒棱)
无论探头采用哪种材料制造,最基本的要求都是确保在数据采集的温度范围内自始至终地与热电偶接触。生成的冷却曲线派生的数据被用于计算传热系数和整个淬火过程中的温度分布情况。精确的计算需要精确的时间-温度数据,这意味着必须以很短的时间间隔记录真实的温度。测温过程中对时间间隔延迟影响最大的因素是热电偶尺寸、制作材料和整个淬火过程中热电偶与探头的接触情况。
使用最广泛的是铠装热电偶,它有一层保护热电偶线的金属套。铠装热电偶的参数包括尺寸,测量接点设计、外套和绝缘材料。大多数用于钢热处理的热电偶可以在约 200-1200℃(-330-2190°F)的温度范围内使用。通常将测量接点焊接到探头材料上以得到最好的热电偶响应。腾西等人报道,采取下列措施可以得到最小的时间延迟和温度失真:
1) 确保探头与热电偶之间有最佳的连接。
2) 热电偶孔的尺寸最小化,孔越小,热电偶链接得越好。
3) 探头材料和用来连接热电偶的材料应具有类似的热力学性能。
4) 通过将热电偶线焊接到探头上来确保温度延迟最小。
5) 推荐使用外径为0.5mm (0.02in) 的铠装热电偶。
6) 在焊接到外套上的测量接点处使用导热胶并不能提高灵敏度。选定了数据采集系统和探头设计与材料之后,将探头加热到合适的温度并浸入要研究的淬火冷却介质中。收集 温度-时间数据,可以得到一条时间-温度 冷却曲线,能说明在表面发生的不同冷却机制,下面将对冷却曲线进行分析。
1.4 冷却曲线分析
冷却曲线分析的第一步,是对相同试验条件下得到的时间-温度冷却曲线进行目测比较分析。这种目测分析的目的,主要是得到不同特征的冷却过渡所需要的时间和发生时的温度。对于不同的淬火冷却介质和淬火条件,可以将感兴趣的冷却曲线叠加起来进行比较评估。比较分析冷却曲线数据有很多方法,目前最常用的方法有两种。第一种方法是冷却曲线参数化,腾西建议的参数包括:
1) 膜沸腾转变到核沸腾的时间tA-B(s) 。
2) 膜沸腾转变到核沸腾的温度TA-B (℃) 。
3) 膜沸腾转变到核沸腾的冷却速率 CRDHmin(℃/s ) 。
4) 700℃时的冷却速率CR700(C℃/s) 。
5) 最大冷却速率 CRmax(℃/s)。
6) 最大冷却速率时的温度TCRmax(℃) 。
7) 300℃时的冷却速率CR300(℃/s) 。
8) 冷却到300℃所需的时间t300(s) 。
9) 200℃时的冷却速率CR200(℃/s) 。
10) 冷却到200℃所需的时间t200 (s) 。
参数1)~3)与全膜沸腾(蒸汽膜沸腾)向核沸腾转变的时间和温度及临界温度下的冷却速率有关。之所以要测量 700℃时的冷却速率(参数4)) ,是因为通常人们都希望尽可能提高这一冷却速率以避开钢的珠光体转变区域(鼻子尖)。参数5)和6)分别是最大冷却速率及其发生的温度。一般来说,人们希望CRmax、越大越好,而TCRmin越低越好。某些温度时的冷却速率以及冷却到这些温度所需的时间的冷却速率,如300℃和200℃ (参数7)~10)) , 也经常被测定,因为它们关系到钢的开裂和变形倾向。为减少变形和开裂,人们希望这个区域的冷却速率越小越好。参数7)~10)与马氏体转变区域有关,一般希望这越小越好。这些在图12中有所阐明,并经常用于钢、不锈钢及 Inconel 600 探头上。
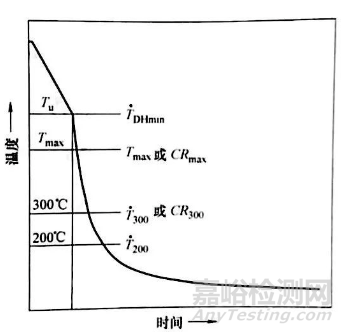
图12 常用冷却曲线的特征参数
对于使用银探头得到的冷却曲线,也有各种不同的冷却参数,但是通常包含以下参数中的两个或更多个:
1) 莱登弗罗斯特温度和冷却速率。
2) 从核沸腾向对流冷却转变的温度。
3) 冷却到600℃ (1110°F) 、400℃ (750°F)和300℃ (570°F) 分别需要的时间。
4) 最大冷却速率和300℃ (570°F) 时的冷却速率。
5) 临界热流密度,可以从冷却曲线中估算出来。
知道冷却曲线分析数据的固有变异性是很重要 的。当无法得到具体的统计数据时,相关报道称有用的数据精度限制是±(8%~10%) ,而通常无法得到完整的统计分析结果。使用图5所示的 Inconel 600探头来试验无搅拌矿物油淬火冷却介质的试验方案,其精度结果是可以得到的。这种变异性的产生有许多原因,其中包括热电偶尺寸、接触情况和反应时间、热电偶孔在探头体中的位置、触发机制以及时间-温度数据采集的开始温度、数据采集速率、探头表面状况、清洁方法、探头在淬火冷却介质中的布置、淬火冷却介质的体积和其他一些因素。再考虑到报告冷却曲线数据的实验室的数量、探头及试验设备供应商的区别等,令人惊讶的是,这种可变性也不算非常大。
二、传热系数计算
本节概述淬火过程中传热系数和热流密度的基本知识。后面将介绍简化方程方法的各种应用实例。例如,将简单形状的钢件淬入液体型可蒸发淬火冷却介质中,分析这一过程中发生的传热,就可以考虑用简化方法来计算冷却时间和冷却速率。并将讨论利用试验得到了准确的淬火过程数学模型、表面温度或表面下温度之后,通过解一个恰当的反问题来计算传热系数(HTC ) 的简化方法。正则热条件理论用于冷却时间和冷却速率的测定,基于它来计算平均传热系数的方法也将得到介绍。需要用到以下符号:

2.1 反问题
反问题领域是由物理学家维克托·安巴尔楚米扬(Viktor Ambartsumian) 首先发现并介绍的,他的逆向建模包括使用试验获得的热导体内的热数据来估计边界条件,如特定温度或热流密度。热传导的反问题依赖于对温度的测量,以估算物理问题中数学公式里的未知量包括边界热流密度、热源、热力学性质、边缘的形状和尺寸等。干扰因素在。于任何一次对温度的测量中,将造成热流密度预测的不稳定性。但是,通过在两个位置测量温度可以较好地改善这一(对热流密度)预测的稳定性。因为解法对试验测得数据中的随机误差很敏感,所以“不适定问题”的求解需要用到“正则化技术” (regularization technique) 。
2.1.1 吉洪诺夫(Tikhonov) 正则化方法
热传导反问题的成功求解方案通常需要(将其)重置成“近似适定问题”, 经常采用最小二乘法 。正则化方法有很多种,其中就包括吉洪诺夫正则化方法,这种方法是将一些平滑项加入最小二乘方程来减少由测量误差造成的不稳定性。吉洪诺夫从理论上证明,使用这种方法可以将反问题正确地解出。由于淬火过程中的传热非常复杂,需要做一些附加的调查研究以进一步改进热传导反问题的求解。
2.1.2 求解反问题的格林(Green) 函数方法
古塞伊诺夫(Guseynov) 也用格林(Green) 函数方法解决线性和非线性反问题。这种方法被用来求解热传导双曲线方程之类的非线性反问题,在这种问题里,数学模型中的一些参数不能由试验得到,但能够通过精确计算得到。
2.1.3 统计学正则化方法
克里沃希(Krivoshey) 求解反问题时使用的是一种随机方法,假定数学模型中的所有参数都有一种随机性。它用于求解第四种传热模式的反问题。
2.1.4 求解热传导和质量传递反问题的一般方法
科瑞考斯基(Krukovskyi) 使用了牛顿-高斯(Newton-Gauss) 和吉洪诺夫方法。在美国广泛使用一种由贝克(Beck) 等人所推荐的求解反问题的新方法,而吉洪诺夫方法在欧洲则广为人知。求解第一种传热模式的反问题的结果,通常以传热系数(HTC) 与表面温度的关系的形式呈现,如图13所示。这些传热系数(HTC) 被用在计算淬火过程中,包括决定钢相变的冷却时间和冷却速率值。
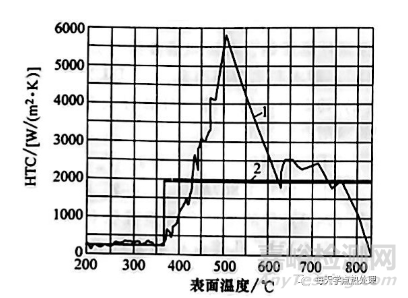
图13 传热系数与表面温度的关系
MZM-16油,油温61℃ (142F) ,试样:Φ19.9mm×80mm
1一求解反问题 2一正则热条件理论
2.1.5 正则热条件理论
正则热条件理论被用来计算平均传热系数、任何形状钢件的冷却时间和冷却速率。图13所示为用孔德拉特耶夫(Kondratjev) 正则热条件理论计算的平均传热系数。孔德拉特耶夫理论已经被用来计算核沸腾过程中的平均有效传热系数。在这种情况下,传热系数仅可用于计算钢件中心部位的冷却时间和冷却速率。随后将讨论核沸腾期间的简化计算方法,以及冷却时间和冷却速率的计算方法。
2.2 简化计算方法
2.2.1 第二种传热模式的数学模型
非稳态热导率由方程给出,即:

为使钢件淬火后变形最小,应完全消除局部膜沸腾。如果qer1 最大化,则膜沸腾就可以被消除。已经确定的是,盐水溶液存在一个最适合的浓度,淬火油存在一个最适合的温度,此时第一临界热流密度(qcr1) 最大化,如图14和图15所示。因此,可以通过优化临界热流密度来优化淬火工艺,而临界热流密度越大越好,以消除局部膜沸腾,消除局部膜沸腾又可以显著减少变形。
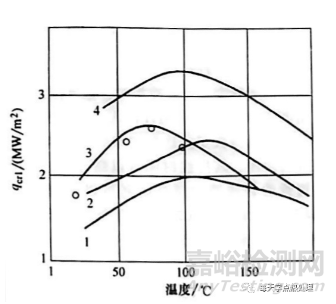
图14 第一临界热流密度(qcrl)与矿物油温度(T) 的关系
1-MZM-120 2-MS-20 3-Effectol
矿物淬火油 4-MZM-16
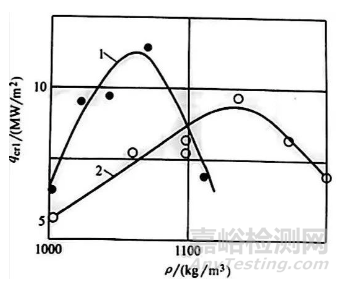
图15 第一临界热流密度(qcrl)与盐水溶液密度(p) 的关系
1-NaCI水溶液 2-LiCI水溶液
当全膜沸腾结束且没有局部膜沸腾时,核沸腾的边界条件可以写成:

注意:在沸腾阶段必须考虑到AT=Tsf-Ts, 而不是AT=Tsr-Tn, 因为临界形核半径Rcr仅取决于边界层的过热度,其计算公式为:

式中,Rcr是气泡能够长大和聚集的临界尺寸。
活跃的核心是热量的基本载体,它们将热量从表面转移到冷的液体里。在对流冷却阶段中,边界条件类似于膜沸腾阶段的边界条件:
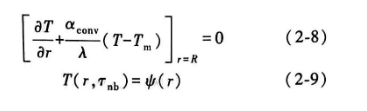
从核沸腾转变到对流冷却时,qnb=qconv。由图16可见,在钢件淬入 NaOH 水溶液的过程中,膜沸腾消失了。这里初始的传热模式是短暂的核沸腾阶段,其持续时间可以通过式(2-10) 计算。短暂的核沸腾的持续时间可以结合边界条件[式(2-6) ] 解出式(2-1) 来计算。沸腾阶段的持续时间可以通过科巴斯科(Kobasko) 方程[式(2-5) ] 来计算
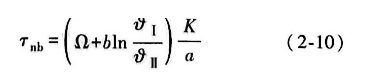
式中,b=3.21 。

为了保证计算正确,必须知道β 值[式(2-11) 、式(2-12) ] 。对水和水溶液而言,可以认为 β=3. 45 。
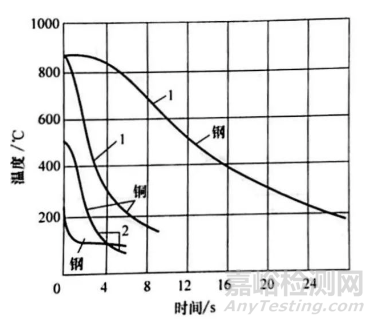
图16 Φ38.1mm (Φ1.5in) 的球在5%的 NaOH水溶液中淬火时温度随时间的变化曲线
2.2.2 冷却时间的计算
计算任何形状钢件冷却时间的通用方程如下:
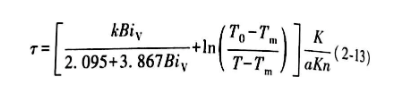
式(2-13) 中的主要参数是孔德拉特耶夫形状因子K (表4 ) 、孔德拉特耶夫数Kn和广义毕渥(Biot) 数Biy;平均热扩散系数a是一种材料特性。
式(2-13) 中的孔德拉特耶夫数Kn是广义毕渥(Biot)数Biy的函数,即:

2.2.3 冷却速率的计算
任何形状钢件心部的冷却速率可以由下式计算:
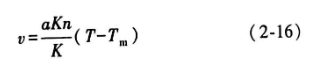
式中,v-冷却速率(℃/s) ;a-热扩散系数;Kn-孔德拉特耶夫数(无量纲);T-温度(℃) ;Tm-浴温(℃) ;K-孔德拉特耶夫形状因子,对于无限长圆柱体,K=R2/5.784。
一些对钢件冷却时间的计算有用的数据见表4 。Inconel600和304奥氏体型不锈钢的热力学性能见表5。
表4 不同形状钢件的孔德拉特耶夫形状因子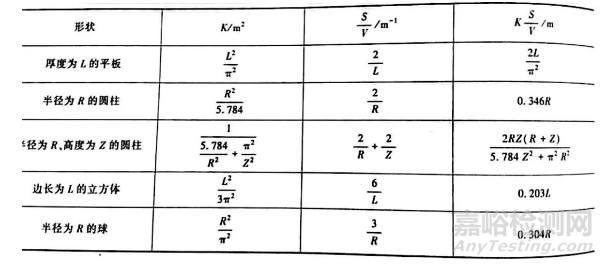
表5 Inconel 600和304不锈钢随温度变化的热导率和热扩散系数
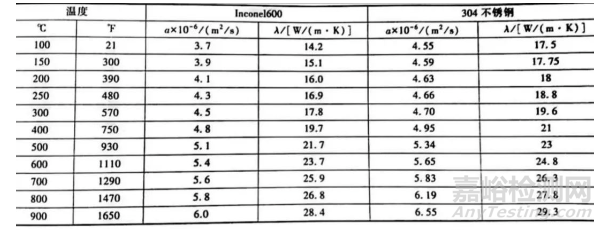

来源:每天学点热处理


