简介

 

纤维增强复合材料因其广泛的应用领域而受到重视，它们在交通、能源和消费品等行业中扮演着关键角色。与传统的单一材料相比，纤维复合材料能够根据特定的应用需求定制其特性。除了宏观层面的评估，结构复合材料还需要进行微观层面的应力和失效分析，这有助于识别层压结构中的关键因素。

 

复合材料的分析可以在宏观和微观两个层面进行，每种方法都有其独特的优势和限制。通过实施多尺度分析，可以更全面地理解复合材料结构及其组成元素在不同层面上的反应。这种分析方法对于探究在宏观载荷作用下的微观失效机制尤为重要。

 

在复合材料的失效分析领域，传统的连续介质方法虽然在多数情况下能够提供有效的预测，但在关键工程应用中，对精度的要求往往更高。因此，将力学失效理论应用于材料的微观结构层面，通过细观力学方法来探究单个组分的失效行为，可以为复合材料的失效预测提供更为精确和深入的理解。这种方法能够揭示微观尺度上的失效机制，从而为复合材料的设计和性能优化提供更为详尽的科学依据。

 

细观力学分析

 

本案例聚焦于单向代表性体积单元（Representative Volume Element, RVE）的细观力学行为分析，旨在通过该分析揭示其宏观均质化材料特性。所研究的复合材料由单向排列的石墨纤维嵌入环氧树脂基体构成，其中纤维与基体间的界面层具有极薄的厚度。通过细观尺度的力学模拟，探究该界面层对复合材料整体性能的影响，以及如何通过细观结构设计优化其宏观力学响应。

 

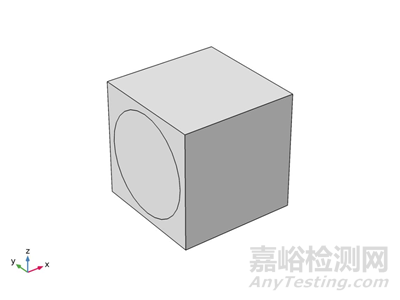
图1 带有石墨纤维、薄界面和环氧树脂基体的基本单元几何形状

 

图1展示了一个典型的单向代表性体积单元（RVE），其中心位置放置了一根圆柱形的石墨纤维。在给定纤维体积分数为60%的条件下，通过数学建模和计算方法确定该纤维的几何半径参数。这一参数对于理解纤维在复合材料中的力学行为及其与基体的相互作用至关重要。

 

层合板的构造由多层材料组成，每层包含T300型号的石墨纤维、DY063型环氧树脂以及特别设计的界面材料。在此模型中，石墨纤维被假设为横向各向同性材料，并以正交各向异性材料进行模拟；而界面材料和环氧树脂则被视为各向同性材料。在纤维增强复合材料的微观结构中，界面区域由纤维和基体的近表面层以及这两个表面之间的过渡材料层组成。界面的力学性能，无论是过于薄弱还是过于刚硬，均会对复合材料的整体性能产生显著影响。因此，选择具有最佳力学性能的界面材料对于提升复合材料的综合性能至关重要。本模型中，界面的弹性属性被设定为介于纤维和基体之间，既不过于刚硬也不过于柔软，以期达到最佳的力学匹配效果。

 

 

在本研究案例中，对于纤维增强复合材料的细观力学分析，并未直接对纤维与基体之间的界面进行显式几何建模。相反，通过在固体力学接口中引入薄层节点，以隐式方式考虑界面的存在。该薄层节点具备一个线弹性材料子节点，负责对界面的弹性响应进行表征。这种处理方式使得界面的力学行为能够间接影响复合材料的均质化材料属性以及局部应力分布。

 

进一步地，为了实施细观力学分析，本研究利用固体力学接口中的单元周期性节点，在代表性体积单元（RVE）的三对面施加周期性边界条件。通过这种方式，可以模拟复合材料在宏观尺度上的连续性和均匀性。为了从RVE中提取均质化的弹性矩阵，本研究设计了六种不同的载荷工况，并对RVE进行响应分析。通过选择特定的平均应变周期类型，可以有效地获得复合材料的均质弹性矩阵，从而为进一步的力学行为预测提供基础。

 

宏观力学分析

 

在层合板的分层理论中，自由度被定义为参考表面（或建模表面）上的位移分量，包括平面内的u和 v以及垂直于参考面的w方向。该理论在本质上与三维固体弹性理论保持一致，但通过引入层间剪切应力的概念，它能够更精确地描述层合板的力学行为。分层理论的优势在于其能够捕捉并分析层间剪切应力的分布，这对于模拟和预测厚复合材料层合板的应力状态至关重要。此外，该理论在研究层合板中的脱层现象，即层间分离问题时，提供了一种有效的分析工具，因为它能够揭示脱层过程中的应力变化和传递机制。

 

在本研究中，所构建的模型涉及一个复合材质的圆柱形结构，其几何特征为长度0.5米、半径0.1米，如图2所示。该模型的边界条件和受力情况具体如下：

 

圆柱体的一端施加了固定约束，以模拟实际结构中的支撑条件。

 

相对端面上施加了50千牛的横向力，该力以均匀分布载荷的形式作用于圆柱体的横截面上，以模拟外部荷载对结构的影响。

 

这种设置允许对复合材料圆柱体在受横向载荷作用下的应力和变形行为进行详细的力学分析。

 

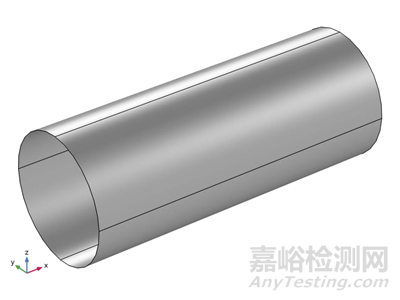
图2带边界条件和载荷的几何形状

 

如图3所示，所研究的层合板结构由四层材料构成，每层厚度为1毫米，每层材料的特定取向是根据其在层合板中承担的力学角色和预期的性能要求精心设计的。

 

图3 四层层压材料的全厚度视图

 

如图4所示，层合板的构造由四层材料组成，每层厚度一致，且沿层合板的基准坐标系，各层的纤维方向依次为垂直（90度）、水平（0度）、再次垂直（90度）和水平（0度），从层合板的底部起始。每层材料的方向角是根据其在层合板结构中的力学功能和设计要求来确定的。各层的材料属性，包括弹性模量、泊松比等，均基于先前进行的细观力学分析中计算得到的均质化材料属性。这种分析方法允许将复合材料层合板视为具有各向异性的均质材料，从而为进一步的结构设计和性能评估提供了准确的材料参数。

 

图4 层合板的铺层顺序[90/0/90/0] °显示了各层从下到上的纤维方向

 

在进行复合材料圆柱体在特定载荷作用下的失效分析时，可以采用两种专门针对复合材料的失效判据：Hashin准则和Puck准则。这些准则是复合材料力学领域的先进理论，它们综合考虑了材料在多轴应力状态下的复杂行为，包括在拉伸和压缩载荷作用下可能出现的不同失效模式。具体而言，Hashin准则和Puck准则能够识别和预测复合材料在不同载荷组合下的失效行为，从而为复合材料结构的设计和安全性评估提供了科学依据。表2详细列出了这两种准则所涵盖的失效模式，为复合材料的失效分析提供了明确的参考标准。

 

 

为了探究复合材料在宏观载荷作用下各组分的局部力学响应，本案例沿用了首次分析中采用的代表性体积单元（RVE）的几何构型和材料参数，并设定了第二次分析所需的宏观应变。通过对RVE内多个材料点实施细观力学分析，识别出在宏观层面分析中应力集中或潜在失效的区域。

 

细观力学分析

 

在细观尺度上，考虑到材料组分的相互作用和整体性，可以应用基于力学的失效判据来预测材料的失效行为。这些细观层面的失效判据相较于宏观层面的判据，能够提供更为精确的失效预测。对于纤维增强复合材料，Tsai-Wu正交各向异性失效判据因其考虑了正交各向异性材料的特定力学行为而被认为是较为适宜的选择。在单向纤维增强复合材料中，纤维沿着纵向连续分布，展现出较高的纵向弹性模量和承载能力，从而在纵向拉伸和压缩载荷下承担主要的力学作用。而在横向上，纤维通过基体材料的粘合作用与周围基体结合，基体在横向和剪切载荷中发挥关键作用。若忽略Tsai-Wu判据中横向应力和剪切应力的影响，针对纤维的失效判据可以简化为一个表达式，以便于分析和应用。

 

 

其中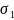，是应力分量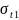，和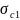分别是层坐标系中的抗拉和抗压强度。

 

在考虑基体材料的力学行为时，必须认识到基体作为各向同性介质，在拉伸和压缩状态下的强度表现存在差异。根据理论分析和实验验证，基体材料的失效行为与偏应力（von Mises应力）和体积应力（hydrostatic应力）紧密相关。在本案例中，基体材料的失效判据将依据这一理论框架进行构建，以确保对基体在不同受力状态下的失效模式进行准确预测和描述。具体而言，本案例将采用一种综合考虑偏应力和体积应力影响的失效准则，以实现对基体材料在复杂载荷条件下失效行为的科学评估。

 

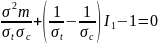
其中，σm是von Mises 应力，I1 是应力张量的第一不变量。

 

在复合材料中，界面失效通常归因于法向和切向作用力超出其承受的强度阈值，这种过度的力作用导致界面发生脱黏现象。基于此失效机制，本研究案例引入了一种针对界面的二次失效判据，旨在定量描述和预测在多轴应力状态下界面的失效行为。该判据综合考虑了法向和切向应力对界面强度的影响，为复合材料界面的失效分析提供了一种科学和系统的方法。通过应用这一失效准则，可以更准确地评估复合材料结构在实际工作条件下的界面稳定性和可靠性。

 

 

其中，tn和ts分别为法向（垂直于界面边界）和剪切（与界面边界相切）牵引力，

 

σn和σs分别为法向强度和剪切强度。法向牵引力周围的角括号是Macaulay括号，如果结果为正，则返回变元，否则返回零。

 

 

结果与讨论

 

在细观力学分析的框架内，本研究案例通过施加六种不同的载荷工况来计算材料的弹性矩阵。如图5所示，选取了其中的四种载荷工况来展示有效（von Mises）应力的分布情况。该图揭示了材料各组分在不同载荷条件下的响应特性。基于首次细观力学分析所得到的均质化材料属性，将作为输入参数应用于随后的宏观力学分析中，以预测和评估复合材料结构在宏观尺度下的力学行为和性能。这一方法允许从细观层面到宏观层面的无缝过渡，为复合材料结构设计和性能优化提供了坚实的理论基础。

 

 

 

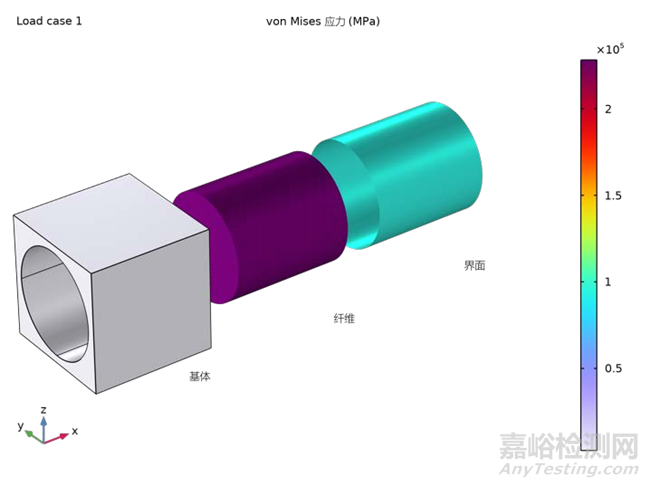
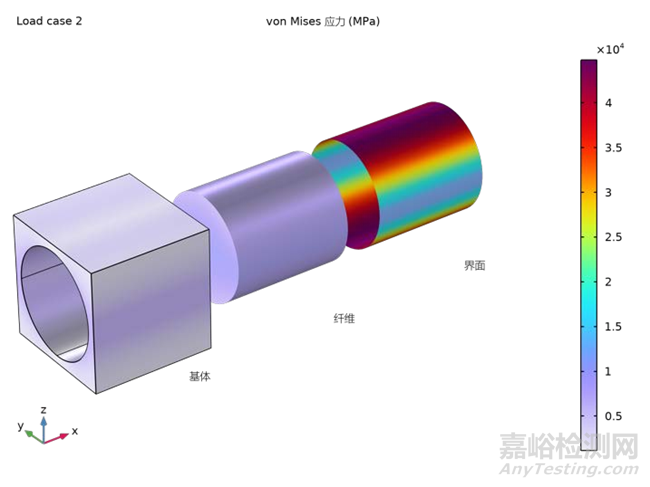
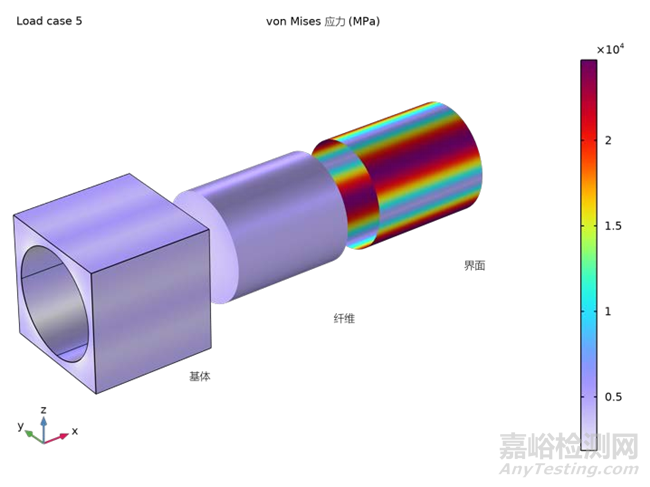
图5四种载荷工况下基本单元中的von Mises 应力分布

 

图6呈现了宏观尺度分析中复合材料圆柱体内部的von Mises应力分布图。根据该图的显示结果，可以观察到圆柱体两端区域的应力值较高，表明这些区域在载荷作用下可能承受较大的力学负荷。这种应力分布特征对于理解结构在实际工作状态下的力学行为至关重要，同时也为进一步的结构强度评估和潜在失效区域的识别提供了关键信息。

 

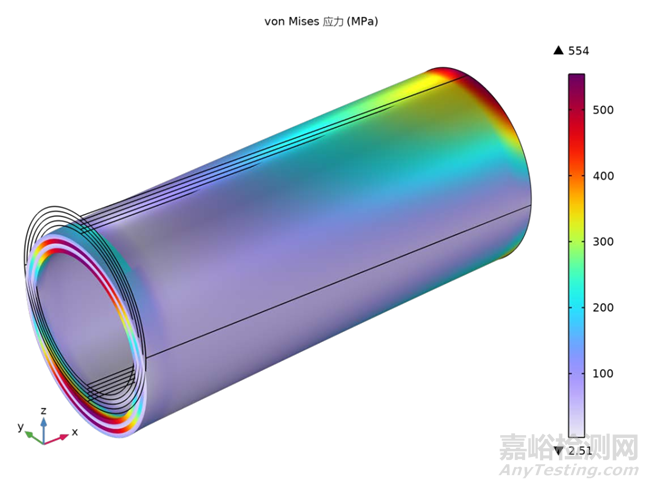
图6 复合材料层合板中的von Mises 应力分布

 

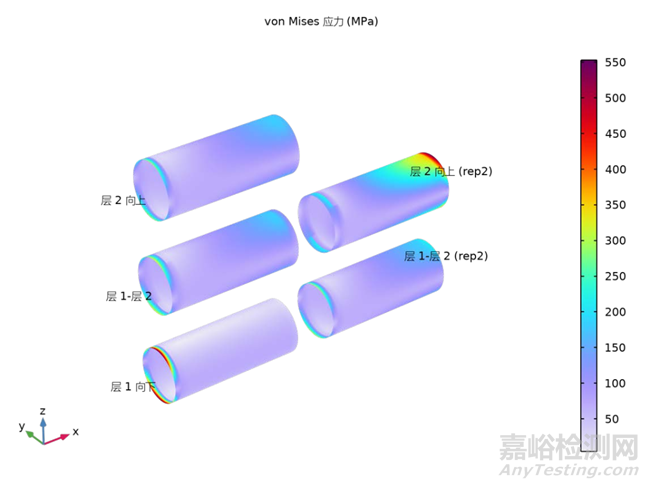
图7描绘了层合板中五个界面处的von Mises应力分布图，该分布揭示了应力集中现象主要发生在层合板的内层或外层。为了精确识别应力峰值的具体位置，本研究采用了表面最大值节点技术。通过这种方法，确定了层合板外层固定端处的应力值最高，表明该区域在载荷作用下可能首先达到其应力承载极限。同时，圆柱体负载端的内层也观察到较高的应力水平。这两个应力集中区域将作为后续细观力学分析的关键点，以进一步探究其对层合板整体性能的影响。

 

 

如图8(a)和图8(b)所示，复合材料圆柱体的Hashin和Puck失效判据的失效指数分布图揭示了失效风险的不均匀性。在Hashin失效准则的应用下，失效指数的最大值出现在圆柱体的外层，且特别集中在朝向载荷端的区域。相对地，在Puck失效准则的应用下，失效指数的峰值则位于圆柱体的第二层，即从内侧向载荷端过渡的区域。值得注意的是，即使在圆柱体的内层和外层，Puck准则同样预测出了较高的失效指数，表明这些区域可能面临较高的失效风险。

 

鉴于Hashin和Puck准则分别考虑了不同的失效模式，因此，对每种失效模式下的失效指数进行细致的评估至关重要。这种评估有助于识别潜在的失效区域，并为后续的细观力学分析提供了关键的失效风险评估信息。内层和外层中材料点的失效指数将作为进一步分析的基础，以探究这些区域在不同失效模式下的响应特性和失效机理。

 

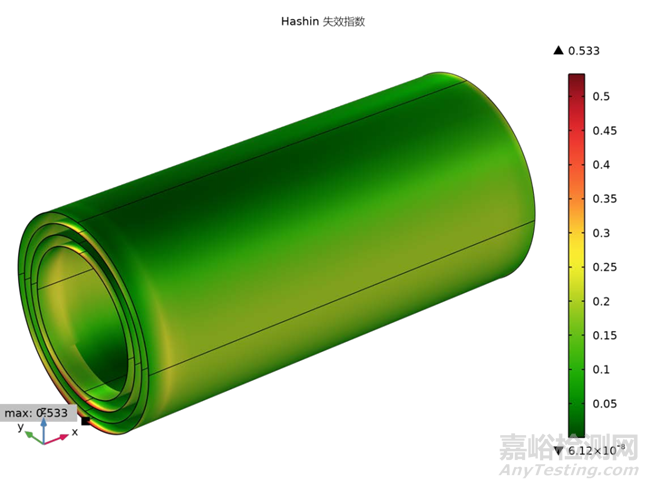
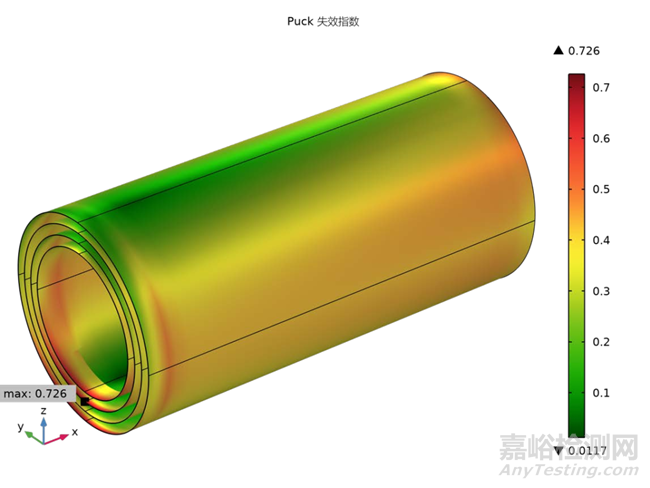
图8 复合材料层合板中的(a)Hashin和(b) Puck失效指数分布

 

表4详细列出了在两种不同的失效准则下，复合材料结构在细观力学分析中的各个失效模式所对应的最大失效指数。这些指数的数值分析结果明确指出，在拉伸载荷作用下，基体材料是该复合材料结构中最先达到失效临界状态的组分。这一发现对于理解复合材料的失效机制和预测其在实际应用中的性能具有重要的理论和实际意义，同时也为复合材料结构的设计优化和性能提升提供了科学依据。

 

 

在第二轮细观力学分析框架内，本研究选定了材料内部的多个关键位置，并对这些位置施加了与宏观应变相对应的应变条件，以此来模拟并获取局部应力和应变场。这一步骤对于深入理解细观尺度上的失效机理至关重要。如图9(a)所示，对内层材料点的成分进行的von Mises应力分析揭示了微观应力远高于宏观应力水平，从而突显了细观力学分析的必要性。

 

进一步地，图9(b)展示了不同材料位置上各成分的应力分布特征。基于宏观力学分析的结果，本研究特别选取了内层和外层朝向载荷端的两个临界点，以进行更为深入的细观力学分析。如图9(c)和图9(d)所示，细观力学失效分析的结果表明，在这些关键材料点上，基体材料的失效指数显著高于纤维和界面，与宏观力学失效分析的结论相一致。

 

此外，细观力学失效指数的值小于1，表明在这些临界点上，材料尚未达到失效状态。这一发现为复合材料结构的安全性评估和设计优化提供了重要的微观层面信息，证实了材料在所选关键点上仍具有足够的承载能力。

 

 

 

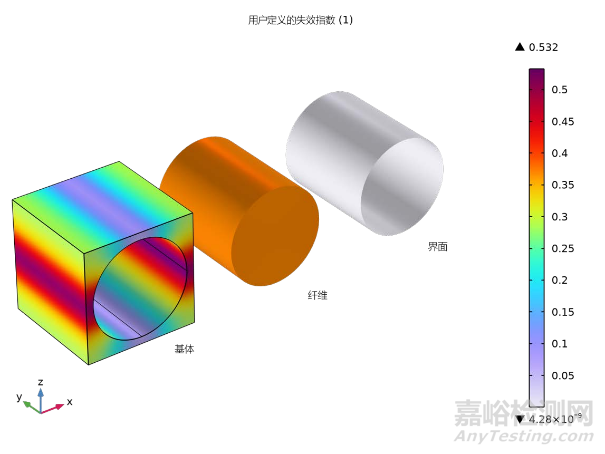
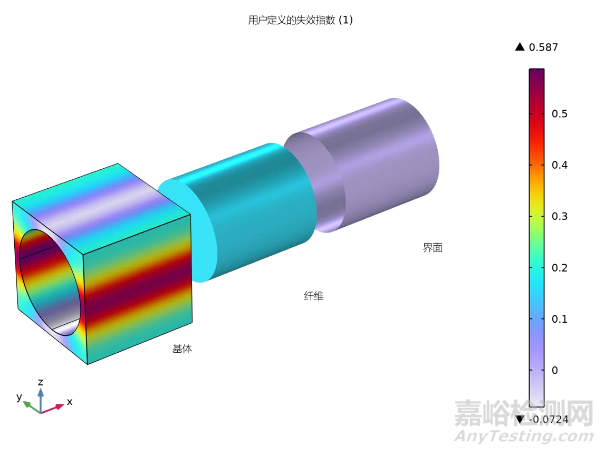
图9 复合材料圆柱体

 

(a)特定材料位置

 

(b)多个材料位置的成分中的von Mises 应力；复合材料圆柱体

 

(c)特定材料位置和

 

(d)多个材料位置的成分中用户定义的失效指数

 

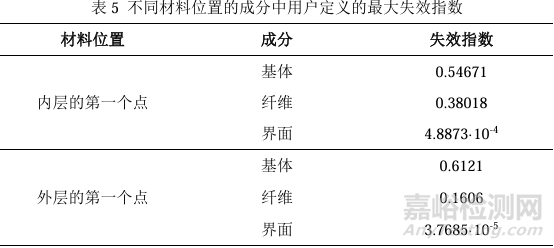
表5详细列出了在宏观力学分析中识别的两个关键材料位置的成分失效指数的最大值。这些位置被选为临界点，意味着它们在结构中承受着较高的应力集中，可能对材料的整体性能产生显著影响。通过分析这些位置的失效指数，可以更深入地理解材料在这些关键区域的失效风险，为复合材料结构的强度评估和优化设计提供重要的数据支持。

 

本研究通过多尺度仿真分析方法，深入探究了纤维增强复合材料在不同载荷工况下的细观力学行为和失效机制。研究聚焦于单向代表性体积单元（RVE）的细观力学行为，分析了石墨纤维、环氧树脂基体以及它们之间的界面材料在宏观载荷作用下的应力和应变分布。通过应用Hashin和Puck失效准则，评估了复合材料结构在拉伸和压缩状态下的失效风险，识别了基体材料在拉伸过程中最可能首先达到失效临界状态。研究结果表明，细观力学分析能够提供材料在关键区域的失效风险评估，为复合材料结构的安全性评估和设计优化提供了重要的微观层面信息。

 

本研究可能的应用场景包括但不限于航空航天领域的轻质高强度结构设计、汽车工业中的高性能部件开发、以及能源行业中承受复杂载荷的复合材料结构的可靠性评估。通过本研究的分析方法和发现，可以指导这些领域中复合材料结构的设计，优化其性能，提高其在实际应用中的可靠性和耐久性。

 

参考文献

[1] Chawla K K .Micromechanics of Composites[J]. 2019.DOI:10.1007/978-3-030-28983-6_10.

 

[2] Ha S K , Jin K K , Huang Y .Micro-Mechanics of Failure (MMF) for Continuous Fiber Reinforced Composites[J].Journal of Composite Materials, 2008, 42(18):1873-1895.