一、导读

连续纤维复合材料由于其刚度高、强度大、重量轻等特点。在各行各业中得到了广泛的应用。然而，多相结构和复杂的制造工艺带来了材料和几何上的不确定性。

近日，国际知名期刊《Polymer Composites》发表了浙江工业大学和之江实验室的研究成果。该研究提出一种新的两级代表性体积单元模型，用于在连续纤维复合材料中生成随机纤维分布结构。论文标题为“Generation of two-level representative volume element model for uncertainty analysis of composite materials”。

二、内容简介

研究团队提出了一种新颖的两级代表性体积单元(RVE)模型，该模型同时考虑了微观尺度和中观尺度的材料和几何不确定性，通过ABAQUS、Python、iSight和Matlab软件的集成来实现模拟仿真。因为单个RVE的边界存在不确定性，使得大RVE(LRVE)中更多的几何不确定性需要考虑。在构建LRVE时，每个RVE都考虑了相邻RVE的几何边界和不确定性，从而提高了RVE之间的连接性。最后，将LRVE的统计特性与其他算法进行比较，验证所提出算法的效率和准确性。

图1 主RVE生成流程

图2 3×3 RVE的LRVE自适应生成

研究团队为了验证算法的有效性，采用了四个统计函数来验证LRVE的有效性，为了比较所提出的LRVE的统计空间特性，生成了纤维体积分数为50％、60％和65％的LRVE微结构。每个LRVE由3×3RVE组成，LRVE的长度和宽度为90um。同时生成了总共10个微观结构。将这些统计结果与使用随机顺序吸附(RSE)算法和完全空间随机模式(CSR)算法的结果进行比较。这些结果是通过最近邻距离、最近邻方向、Ripley的K函数和对分布函数进行计算的。结果表明所提出的算法与RSE算法和CSR算法之间存在良好的一致性，即此文算法生成的纤维分布是随机的。

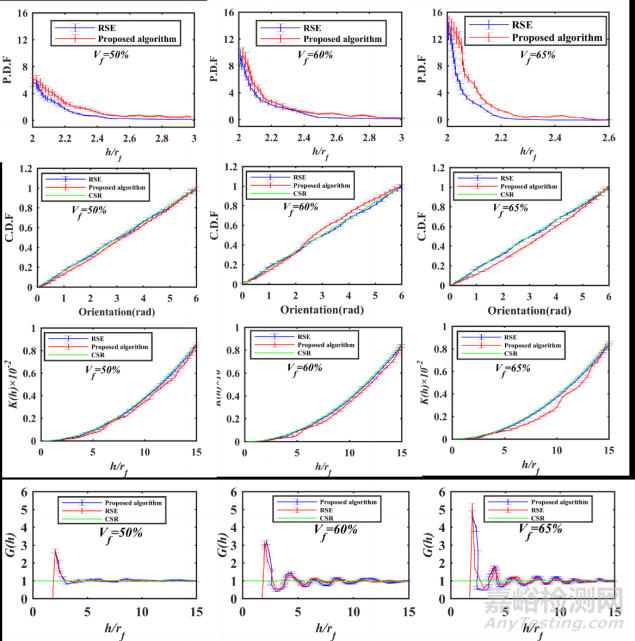
图3 不同纤维体积分数下的最近邻距离、最近邻方向、Ripley的K函数和对分布函数统计结果比较

随后，该研究团队利用连续纤维复合材料的特性预测其有效弹性性能，验证了所开发的LRVE生成算法的有效性。材料的选择为E-glass/ MY750/HY917/DY063，其微观性能的不确定性类型为正态分布。结果表明，该方法预测不确定弹性性能的最大相对误差仅为8.70%，均小于10%。与数值分析结果相比，此算法的预测值更接近实验结果。此外，模型分析得到的泊松比更接近于实验和其他数值方法得到的泊松比结果。

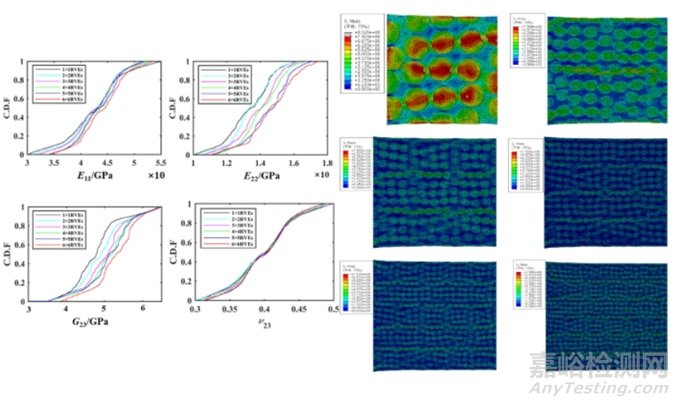
图4 不同数量RVE下宏观弹性性能的不确定性分析

三、小结

该研究提出了一种新的两级RVE模型，用于在连续纤维复合材料中生成随机纤维分布。主RVE采用自适应纤维算法生成，加入不确定边界条件。此外，建立了相邻RVE之间的自适应连接，从而开发了用于两级LRVE的新自适应生成算法。这一研究成果实现了对连续纤维复合材料的多尺度不确定性分析，并为构建数值模型和准确预测连续纤维复合材料宏观尺度不确定性提供了有效途径。

原始文献：

Peng Xiang, Jiang Haohao, Li Jiquan, Jia Weiqiang, Yi Bing, Wu Huaping, Jiang Shaofei. Generation of two-level representative volume element model for uncertainty analysis of composite materials. Polymer Composites, 2024. DOI:10.1002/pc.28831

原文链接：

https://doi.org/10.1002/pc.28831