摘 要: 座椅是汽车内饰件中质量较重的一部分,座椅骨架的轻量化设计可以有效地降低座椅整体质量,提高汽车整体性能.本文利用CATIA 软件对某乘用车前排座椅骨架进行几何建模,建立座椅骨架的有限元模型,并基于国家标准GB 15083—2006 对座椅骨架模型进行有限元分析.然后利用相对密度法的拓扑优化模型对座椅骨架进行轻量化设计,以体积约束下的最小结构柔度为优化目标,通过ABAQUS 软件中的TOSCA 模块对座椅骨架进行拓扑优化,将优化后的座椅骨架结构在ABAQUS 中进行静力学分析.结果显示,在满足座椅结构强度和刚度的情况下,座椅骨架减轻了0.584 kg,减重约4%,实现了座椅轻量化的效果.

 

关键词: 前排座椅骨架;轻量化;拓扑优化;有限元分析

 

汽车的轻量化技术主要是指在不改变汽车原有整体性能下,以轻量化为目标对汽车部件进行设计优化.新型材料的应用对汽车轻量化有着至关重要的影响,汽车的轻量化无论是在环境保护还是提高汽车整体安全性方面都有重要意义.相关研究资料表明: 汽车减少10%整车质量,即可提高6%～8%燃油效率.同时,汽车整体质量的减少也能在一定程度上减轻乘客在碰撞过程中受到的伤害[1].座椅是汽车驾驶室的重要组成部件,也是主要的安全部件[2].汽车座椅作为直接和人体接触的内饰件,对乘客乘坐的舒适性和安全性起着至关重要的作用.但传统座椅设计在充分考虑座椅安全性的同时,往往忽略了座椅整体质量的优化,从而使座椅比较沉重.为更好地提高汽车的整体性能,在保证座椅结构强度和刚度的情况下,座椅减重变得尤为重要.

 

1、 研究现状

对于汽车座椅骨架方面的研究,王淑芬等[3]根据人体工程学的要求,对座椅进行拓扑优化,结果表明,优化后的座椅质量减轻了20%.张光亚等[4]基于拓扑优化理论对后排座椅进行优化,并应用高强度材料,最终使座椅总质量降低了2.585 kg.白煜等[5]提出了一种碳纤维复合材料座椅骨架的设计方法,利用拓扑优化技术合理布置加强筋,最后达到提高座椅刚度和降低座椅质量的效果.张志飞等[6]对座椅骨架进行拓扑优化和尺寸优化,并建立移动最小二乘法模型,利用多目标遗传算法对模型进行求解,优化后的座椅骨架质量下降了5.7%.Oliveira 等[7]对汽车座椅骨架进行拓扑优化,并利用仿真软件和试验验证,在满足座椅强度要求下,使汽车座椅整体质量明显下降,实现座椅轻量化.黄政平等[8]对汽车后排座椅骨架进行拓扑优化和尺寸优化设计,最后在提高座椅骨架刚度的同时,实现了座椅骨架轻量化.刘博勋等[9]应用试验优化方法,以座椅零件的板厚和材料为设计变量,同时建立相应Kriging 模型,并基于此模型使用遗传算法对座椅进行轻量化设计,对比原始模型后,验证了轻量化优化设计方法的有效性.孟礼等[10]分别采用模态分析、形貌优化、拓扑优化和尺寸优化的方法逐步对座椅模型进行优化;在不增加座椅质量的前提下,对部分零件材料进行替换,最后使座椅质量下降了0.31 kg.上述研究主要针对后排座椅背板或前排座椅骨架质量较大的整体部分进行拓扑优化,但未考虑座椅骨架等其他重要零部件的优化设计.

 

本文在对座椅骨架进行多方面考虑的基础上,结合乘用车座椅骨架上其他质量较大且比较重要的零部件进行拓扑优化设计.论文以某车型上的前排座椅骨架为研究对象,采用拓扑优化方法,在保证座椅整体和靠背静强度工况下,分析座椅骨架的应力和应变情况,通过优化得到材料的合理分布;然后在概念设计基础上,对某些应力和应变较大区域应用不同的高强度材料,最后用有限元仿真法对所设计方案进行验证.

 

2、 拓扑优化理论

2.1 轻量化的途径

实现汽车轻量化的方法一般会通过三种途径:结构优化、轻量化材料的应用和先进的制造工艺,其中结构优化和轻量化材料在座椅轻量化设计中被更广泛应用.结构优化又分为拓扑优化、尺寸优化和形状优化,其中拓扑优化对于座椅的减重效果最为明显,其主要是通过有限元分析及优化算法进行静强度的计算与分析,在满足座椅机构强度和使用性能的情况下,尽可能地去除多余材料,合理化座椅在各种工况下的传力路径.

 

另一方面,汽车轻量化材料主要是高强度钢,其抗拉强度是普通低碳钢材2～3 倍,延展性能好,可轧制成很薄的钢板,是轻量化的重要材料.另一类是轻质材料,主要是镁、铝合金、碳纤维等复合材料.轻量化材料应用对于汽车整体减重具有重要意义.

 

2.2 连续体拓扑优化的方法

拓扑优化本质上是在设计区间内合理分布结构材料,在约束条件下使结构柔度和体积最小,或使响应满足一定要求的一种结构设计方法,是将有限元分析和优化方法有机结合的新方法[11].拓扑优化方法从其物理模型描述来说可分为基结构法、均匀化方法、渐进结构优化方法、相对密度法,其相应的优化问题求解方法一般可分为序列线性规划法、优化准则法、移动渐进法、序列二次规划法等[12].

 

相对密度法是结构优化中一种有效的物理描述方法,受均匀化方法启发,其基本思想不是引入微结构,而是引入虚拟相对密度在0～1 之间的可变材料.它借鉴了均匀化方法的经验,直接假设设计材料的宏观弹性常数及其密度的非线性关系.

 

设计变量如下:

 

 

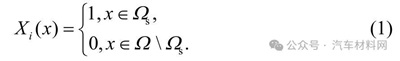
密度和弹性矩阵如下:

 

 

 

式中: Ω 为设计区域;Ωs 为实体区域;Xi(x)为相对密度;ρ0、E0 分别为均质实体的密度矩阵和弹性矩阵.

 

在实际问题中,很难求解这样的离散变量.为解决此问题,引入连续函数 ξ(x) (0 ≤ξ (x) ≤1)来代替离散函数X(x).但在优化过程中,会生成0～1之间的很多单元,因为不存在介于中间密度的材料,所以制造这种结构非常困难,因此需要引入惩罚因子来抑制这种结构的产生.固体各项同性惩罚材料(Solid Isotropic Material with Penalization,SIMP)是在相对密度法基础上提出的,其优化过程中会根据单元相对密度大小决定单元是否存在.在引入惩罚因子后,能够使单元相对密度趋近于0或1的两端[13],从而尽可能地避免中间密度单元的产生,比起相对密度法消除棋盘格的现象,数值稳定方面有很大提高[11].

 

基于SIMP 方法的拓扑优化模型可广泛应用于各种性质的目标函数和约束条件的场合,如最小柔度问题、最小质量、最小体积等问题.

 

2.3 基于SIMP 材料插值的数学模型

以结构最小柔度为目标函数,体积为约束的优化问题数学模型如下:

 

 

 

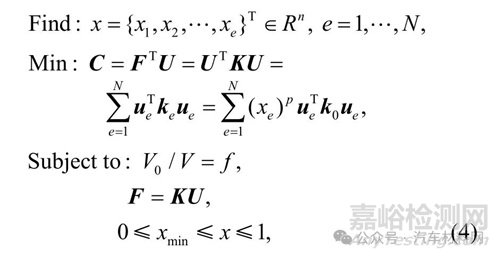
式中: F、U 和K 分别为总载荷矩阵、位移矩阵和总刚度矩阵;ue、ke、k0 分别表示单元位移矩阵、优化后单元刚度矩阵和初始单元刚度矩阵;x 为相对密度,为防止奇异现象的发生,设置其最小值略大于0;N 为总单元数;f 为体积分数;V 和V0分别指优化后的材料体积和初始材料体积;p 为惩罚因子,通常取p=3 .

 

在优化算法求解中,往往需要求解目标函数和约束函数的敏度值,此时可使用柔度目标函数和体积约束函数分别对设计变量求导,由此得到敏度方程.

 

结构柔度敏度方程为:

 

 

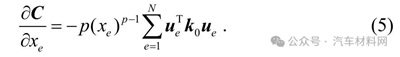
体积约束敏度方程为:

 

 

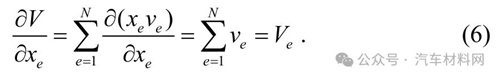
由目标函数以及约束条件构成的拉格朗日函数能够推导出相应优化准则法公式[12],由体积约束条件可求得拉格朗日因子.拉格朗日函数在满足Kuhn-Tucker 的条件下构造出迭代公式:

 

 

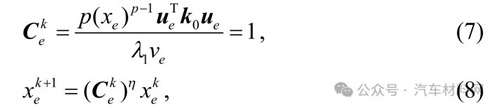
式中: η 为阻尼系数,其作用是能够保证数值计算趋于稳定和收敛.其中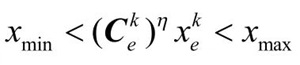,为避免奇异,xmin 不能为零,一般取0.001.

 

在上述迭代过程中,不断地更新设计变量xe,在约束条件下迭代结果不断收敛,最后得到最优的结构设计.

 

3、 座椅骨架有限元模型的建立与分析

3.1 建立模型

以某款汽车前排座椅为参照,使用CATIA 软件建立座椅的几何模型.因为座椅骨架大部分是由钣金件和管件组成,所以采用壳单元进行仿真分析,其中悬挂弹簧和坐垫弹簧采用梁单元模拟,头枕杆采用实体单元模拟.结合座椅整体尺寸,采用平均5 mm 的网格单元,最小单元不小于2 mm,最大单元不大于10 mm,最后得到座椅有限元模型中,共有47 962 个单元,41 938 个节点.座椅骨架几何模型如图1 所示.

 

 

 

图1 座椅骨架几何模型

 

实际座椅上零件一般都采用焊接和螺栓方式连接.模型中焊接采用spotweld的Rigid进行刚性连接,螺栓采用connection of bolt 进行连接,并对座椅骨架整体刚性影响不大的调高泵和调角器等部件进行简化,最终骨架的有限元模型如图2 所示.

 

图2 座椅骨架有限元模型

 

3.2 仿真分析

(1)根据国标GB 15083—2006[14],在座椅总成静强度分析时,需要在座椅质心处分别向前或向后施加20 倍座椅总质量的重力载荷(20 Mg,其中,M 为座椅总质量,g 为重力载荷),要求座椅和座椅安装点应能承受此载荷,不得发生座椅与固定点平面分离的情况.

 

(2)国标GB 15083—2006 还规定在进行座椅靠背强度分析时,对座椅靠背施加相对于座椅R点大小为530 Nm 的载荷,座椅及座椅固定点需要能够承受该载荷,而固定装置、调节装置、锁止机构不能打开[14].

 

对地板连接板和下滑轨后端孔处施加全约束,模拟座椅和车身连接,建立座椅静强度工况下的有限元模型.通过Hypermesh 中post 面板summary工具找到座椅质心(1.149 14E+03,-3.639 92E+02,2.093 47E+02),在质心处分别加载向前或向后的3 900 N 载荷.座椅靠背在静强度工况下,可以简化为载荷力施加在靠背U 型管的集中点P 处,P 点与R 点的距离为609.285 mm,且P 点与R 点连成的直线与竖直方向夹角为37.515°,P 点和R 点的载荷加载情况和位置如图3 所示.图中对座椅靠背施加相对于座椅R 点大小为530 Nm 的载荷力,其等效为在P 点上施加向1 097 N 的水平力.

 

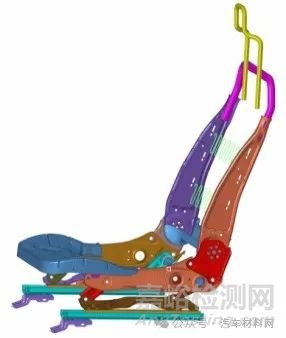
图3 仿真模型的载荷加载

 

不同工况下的仿真结果如图4 和图5 所示.从仿真结果可见,座椅各零件应力都没有超过其屈服强度,头枕杆位移也均小于20 mm.座椅和靠背静强度工况下的应变分别为1.316E-03 和1.858E-03,均没有超过0.2,由此可见,零件失效风险很小.

 

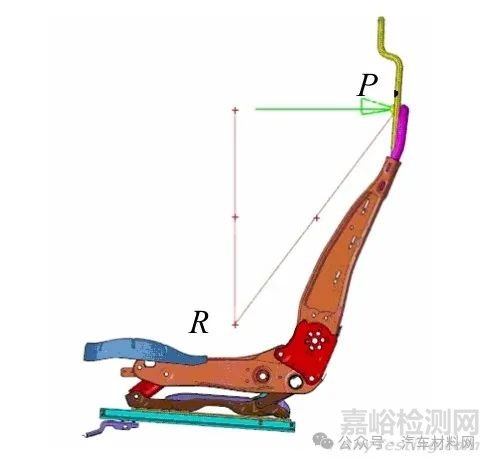
图4 20 倍座椅质量载荷下的结果图

 

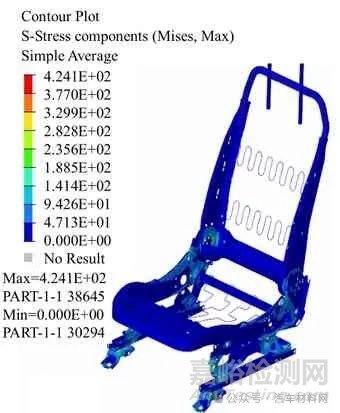
图5 等效530 Nm 载荷 下的结果图

 

3.3 座椅骨架主要部件的拓扑优化

根据仿真结果发现,座椅大部分部件的应力值远小于其屈服强度,所以可选取应力较小的部件作为拓扑优化主要对象.选取靠背侧板、调角器连接板、靠背侧板连接板、坐垫侧板、滑轨支架作为拓扑优化的设计空间,以座椅整体最小应变能作为优化目标,同时,零件体积为约束条件.

 

根据上文建立的拓扑优化模型,对坐垫侧板进行拓扑优化,约束体积分数取0.7,利用ABAQUS的TOSCA 对座椅骨架进行优化,最小成员尺寸取10 mm.设置最小成员尺寸的目的是用来保证零件的可制造性,防止产生棋盘格现象[15].相应的优化迭代曲线如图6 所示,由图可见,座椅骨架的应变能在拓扑优化迭代过程中渐渐变小,逐渐趋于收敛状态.

 

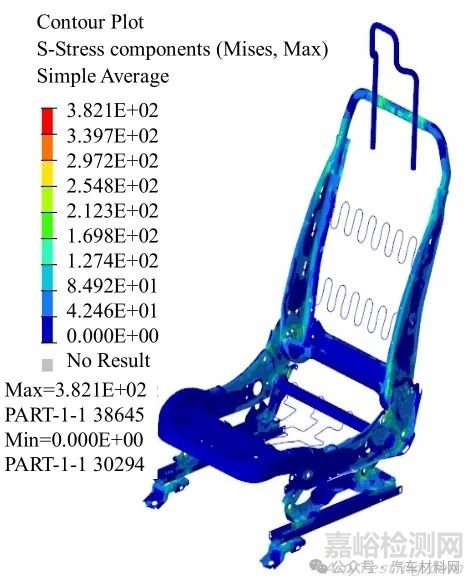
图6 目标函数迭代曲线

 

由于拓扑优化运用SIMP 相对密度插值模型,其相对密度值0～1 从小到大也决定了材料存在的重要性,因此可去除相对密度0.3 以下的伪密度材料,并参考拓扑优化结果去除不重要的单元材料.图7 即为座椅坐垫侧板拓扑优化前后的对比.

 

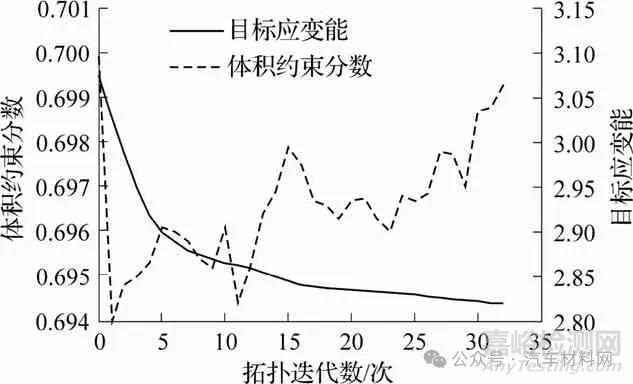
图7 坐垫侧板拓扑优化前后对比

 

图8 为靠背侧板拓扑优化前后对比.在骨架靠背侧板优化过程,为保证侧板部件在实际生产中的可制造性与其他零件的配合性,在优化过程中将零件边缘部分设置成为冻结区域.在去除优化过程中相对密度低于0.3 的材料后,最终结果如图8 所示.

 

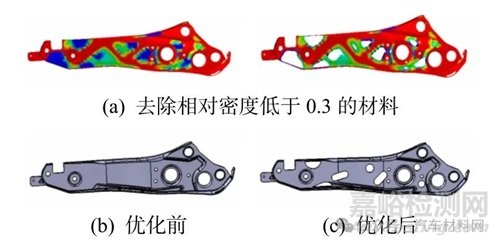
图8 靠背侧板拓扑优化前后对比

 

由于在仿真过程中发现滑轨连接支架的平均应力值比较小,此时可尽量多地去除低密度材料.图9(a)为经过拓扑优化后,最后去除相对密度0.6以下材料后的结果.由于剩下密度材料比较少,实物制造也比较困难,因此最后简化的实物如图9(c)所示.

 

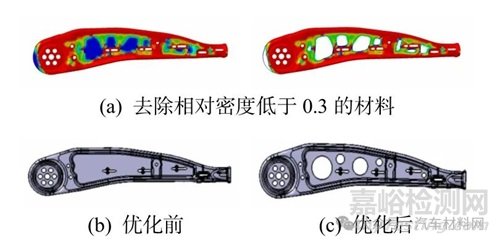
图9 滑轨连接支架拓扑优化前后对比

 

图10为靠背侧板连接板去除相对密度低于0.3材料后的拓扑结构,优化后的实物如图10(c)所示.

 

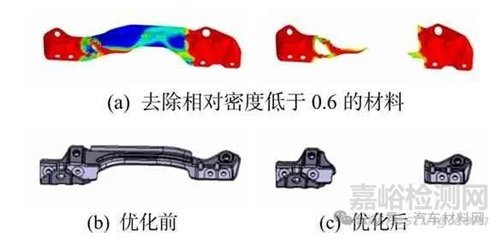
图10 侧板连接板优化前后对比

 

以上是座椅骨架主要零部件进行拓扑优化的方法和过程,此后则可根据拓扑优化的结果对零件实物进行优化设计.

 

4、 优化结果分析

为保证优化后的座椅骨架能够满足强度和刚度的要求,并且关键零件不能失效,不能有突出的尖点,需要对优化后的座椅骨架再一次进行验证.根据上文载荷加载方式对模型进行仿真分析,求解模型的应变、应力和变形.拓扑优化后的有限元座椅骨架模型如图11 所示.

 

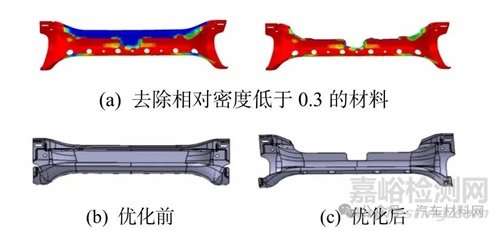
图11 拓扑优化后的有限元模型

 

通过对拓扑优化后的模型进行分析,得到优化后座椅最大应变为2.079E-03,和轻量化前相比略有增大,但都小于0.2,说明零件失效风险较小.

 

经过拓扑优化后得到座椅最大应变如图12 所示,优化前后的部分零件相关应力数据见表1.

 

表1 座椅骨架部分零件优化前后应力对比 MPa

 

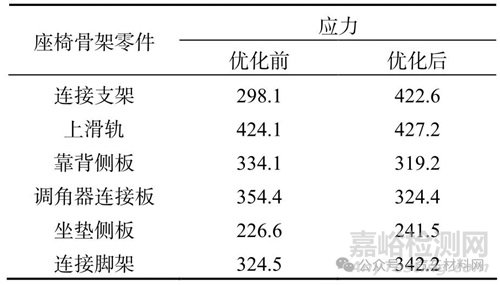
图12 拓扑优化后座椅骨架最大应变

 

由表1 可见,滑轨的连接支架优化前后应力值变化较大,优化后应力值为422.6 MPa,超过其材料屈服强度420 MPa,所以将滑轨连接支架原材料QSTE420TM 替换为S500MC.而其余零件优化后应力值均没有超过材料的屈服强度.由于头枕杆位移量远小于危险值(102 mm),因此优化后增加的位移量可忽略不计.

 

以座椅整体柔度最小为优化目标,零件的体积为约束条件,通过对座椅零部件进行拓扑优化,去除零件多余材料,拓扑优化前后座椅骨架质量减少了4%,头枕位移增加了2.7%,结果均在安全要求范围内,最终实现座椅骨架的轻量化.

 

5、 结论

针对某款汽车前排座椅进行建模,并建立有限元模型,根据GB 15083—2006 对有限元模型进行分析,并根据法规要求对模型设置约束、接触和载荷条件,确定对座椅骨架质量影响较大的座椅零部件.分析了采用SIMP 相对密度插值的拓扑优化模型,以单元密度作为设计变量,结构最小柔度为优化目标,基于ABAQUS中TOSCA模块对座椅骨架进行拓扑优化.最后在满足座椅结构强度和刚度及各零部件都不失效情况下,座椅骨架质量减少0.584 kg,取得了座椅轻量化的效果.

 

来源：期刊：《宁波大学学报（理工版）》 作者：葛 孩1 ,李国平1* ,娄军强1 ,熊文军2 ,肖作华2（1.宁波大学 机械工程与力学学院,浙江 宁波 315211: 2.浙江天成自控股份有限公司,浙江 台州 317201）