实验数据的处理方法

通过实验测得原始数据后需要进行计算将最终的实验结果归纳成经验公式或以图表的形式表示，以便与理论结果比较分析。因此由实验而获取的数据必须经过正确的处理和分析，只有正确的结论才能经得起检验。下面介绍这方面的基本知识。

一、有效数字与运算规律

二、实验数据的误差分析

三、实验数据处理（列表法、图示法）

四、实验数据的方程表示法

在化工实验数据处理中，除了用表格和图形描述变量的关系外，常常需要将实验数据或计算结果用数学方程或经验公式的形式表示出来。

在化学工程中，经验公式通常都表示成无因次的数群或准数关系式，确定公式中的常数和待定系数是实验数据的方程表示法的关键。

经验公式或准数关系式中的常数和待定系数的求法很多，下面介绍最常用的图解法、选点法、平均值法和最小二乘法。

1、图解法

图解法仅限于具有线性关系或非线性关系式通过转换成线性关系的函数式常数的求解。首先选定坐标系，将实验数据在图上标绘成直线，求解直线斜率和截距，而确定线性方程的各常数。

（1）一元线性方程的图解

设一组实验数据变量间存在线性关系：y=a+bx。通过图解确定方程中斜率和截距，如图3-11所示。在图中选取适宜距离的两点，直线的斜率为：。直线的截距，若坐标轴的原点为0，可以在轴上直接读取值（因为,）。或可用外推法，使直线延长交于纵轴于一点，则为直线的截距。否则，由下式计算：

                                （3-16）

以上式中,是从直线上选取的任意两点值。为了获得最大准确度，尽可能选取直线上具有整数值的点，,两点距离以大为宜。

若在对数坐标上用图解法求斜率时请注意斜率的正确求法。

（2）二元线性方程的图解

若实验研究中，所研究对象的物理量即因变量与两个变量成线性关系，可采用以下函数式表示：

上式方程为二元线性方程函数式。可用图解法确定式中常数：。首先令其中一变量恒定不变，如使视为常数，则上式可改写成：=。

式中常数。

由与的数据可在直角坐标中标绘出一直线，如图3-12所示。采用上述图解法可确定的系数。

在图3-11中直线上任取两点，则有：

当求得后，将其代入原式中并将原式重新改写成以下形式；

令，可得新的线性方程：

由实验数据和计算得，由与在图3-12中标绘其直线，并在该直线上任取两点。由f₁,f₂两点即可确定两个常数：

在确定时，其自变量应同时改变，才使其结果覆盖整个实验范围。

2、选点法

选点法亦称联立方程法，此法适用于实验数据精度很高的条件下，否则所得函数将毫无意义。具体步骤是：

（1）选择适宜经验方程式，

（2）建立待定常数方程组

若选定经验方程式为：

则从实验数据中选出两个实验点数据代入上式中得：

（3）联立求解以上方程，即可解得常数。

选点法也可与图解法结合起来。先将实验数据标绘在坐标纸上，在实验数据点之间用一直尺画出一条能代表所有数据的直线，该直线两侧的实验点均匀分布接近直线，在这直线两端选取两点，将其代入经验公式，解联立方程即可求出常数。

3、平均值法

当函数式是线性的，或者可线性化，则该函数适合。列出条件方程 ,使条件方程的数目等于已知的实验个数，然后按照偶数相等，或奇数近似相等的原则，将条件方程相加，得出下列两个方程。

解之，即可求得系数和的值。

例：由传热实验得Re与的一组数据

其经验方程式：

试用平均值法确定其中的系数。

解：对经验公式取对数后使其线性化，得：

上述数据取对数

根据上述数据分成相等两组，然后再相加

解此方程组

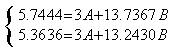
得：

所以所求的准数方程式为：

4、最小二乘法

    在图解时，座标纸上标点会有误差，而根据点的分布确定直线位置时，具有人为性．因此用图解法确定直线斜率及截距常常不够准确．较准确的方法是最小二乘法，它的原理是：最佳的直线就是能使各数据点同回归线方程求出值的偏差的平方和为最小，也就是落在该直线一定的数据点其概率为最大，下面具体推导其数学表达式。

    ①一元线性回归

  己知N个实验数据点（χ₁,у₁），(χ₂,у₂)，……，(χ_N,у_N)。

  设最佳线性函数关系式为у=b₀＋b₁χ。则根据此式N组x值可计算出各组对应的у′值

у₁′= b₀  ＋ b₁χ₁

у₂′= b₀  ＋ b₁χ₂

………

у_N′= b₀  ＋ b₁χ_N

而实测时，每个χ值所对应的值为у₁,у₂……у_N，所以每组实验值与对应计算值у′的偏差δ应为

δ₁=у₁ - у₁′=у₁ –(b₀  ＋ b₁χ₁)

δ₂=у₂ - у₂′=у₂ - (b₀  ＋ b₁χ₂)

………………………………

δ_N=у_N - у_N′=у_N - (b₀  ＋ b₁χ_N)

按照最小二乘法的原理，测量值与真值之间的偏差平方和为最小。

最小的必要条件为：

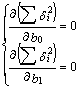
展开可得

= -2[у₁ - (b₀  ＋ b₁χ₁) ] -2[у₂ - (b₀  ＋ b₁χ₂) ] ……… –2[у_N - (b₀  ＋ b₁χ_N) ]

=0

= -2χ₁ [у₁ - (b₀  ＋ b₁χ₁) ] -2χ₂ [у₂ - (b₀  ＋ b₁χ₂) ] ……… –2χ_N [у_N - (b₀  ＋ b₁χ_N) ]

=0

写成和式

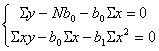
联立解得：

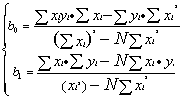
由此求得的截距为b₀，斜率为b₁的直线方程，就是关联各实验点最佳的直线。

② 线性关系的显著检验——相关系数

在我们解决如何回归直线以后，还存在检验回归直线有无意义的问题，我们引进一个叫相关系数(r)统计计量，用来判断两个变量之间的线性相关的程度

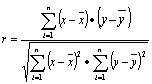
式中：

在概率中可以证明，任意两个随机变量的相关系数的绝对值不大于1。即

∣r∣≤ 1     或  0  ≤∣r∣≤ 1

r的物理意义是表示两个随机变量χ和у的线性相关的程度，现分几种情况加以说明。

当r=±1时，即N组实验值(χ_í,у_i)全部落在直线у′= b₀  ＋ b₁χ上，此时称为完全相关。

当∣r∣越接近1时，即N组实验值(χ_i,у_i)越靠近直线у′= b₀ ＋ b₁χ，变量у与χ之间关系越近于线性关系。

当r=0，变量之间就完全没有线性关系了。但是应该指出，当r很小时，表现不是线性关系，但不等于就不存在其它关系。