实验数据的处理方法

通过实验测得原始数据后需要进行计算将最终的实验结果归纳成经验公式或以图表的形式表示，以便与理论结果比较分析。因此由实验而获取的数据必须经过正确的处理和分析，只有正确的结论才能经得起检验。下面介绍这方面的基本知识。

一、有效数字与运算规律

二、实验数据的误差分析

测得的实验值与真值之差值称测定值的误差，测定误差的估算与分析对实验结果的准确性具有重要的意义。

1．真值与平均值

任何一个被测量的物理量总存在一定的客观真实值，即真值，由于测量的仪器、方法等引起的误差，真值一般不能直接测得，若在实验中无限多次的测量时，则根据误差分布定律，正负误差出现的几率相等，将各个测量值相加并加以平均，在无系统误差的情况下，可能获得近似于真值的数值，因此实验科学给真值定义为：无限多次的测量平均值称为真值。而在实际测量中的次数是有限的，故用有限测量次数求出的平均值，只能是近似真值，称最佳值。在实验测量中使用高精度级标准仪器所测得的值代替真值。常用的平均值有下列几种：

（1）算术平均值

（2）几何平均值

（3）均方根平均值

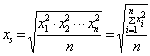
（4）对数平均值

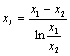
上述各式中：……——各次测量值；——测量的次数。

2．误差的表示方法

（1）绝对误差

某测量值与真值之差称绝对误差，在实际的测量中常以最佳值代替真值。其表达式为：

式中：——绝对误差

  ——次测量值

 ——真值

 ——平均值

（2）相对误差

绝对误差与真值之比称为相对误差。

（3）引用误差

仪表量程内最大示值误差与满量程示值之比的百分数

引用误差常用于表示仪表的精度，按引用误差的大小分成几个等级，把引用误差的百分数去掉剩下的数值就称为仪表的精度等级。测量仪表的精度等级是由国家统一规定的。电工仪表的精度等级分别有：0.1，0.2，0.5，1.0，1.5，2.5和5.0七级。

例如某压力表注明精确度为1.5级，即表明该仪表最大误差为相当档次最大量程的1.5%，若最大量程为0.4Mpa，该压力表最大误差位：

3.误差的性质及其分类

（1）系统误差

在一定的条件下，对同一量进行多次测量时，误差的数值始终保持不变，或按某一规律变化出现的误差，称为系统误差。例如：使用刻度不准、零点未校准的测量仪器；实验状态、环境的改变，如外界的温度、压力、湿度的变化；实验操作人员的习惯与偏向等因素都会引起系统误差。这类误差往往在同一物理量的测定中其大小和符号基本不变或有一定的规律，经过精确的校正可以消除。

（2）随机误差（偶然误差）

在相同条件下，测量同一物理量时误差的绝对值时大时小，符号时正时负，没有一定的规律且无法预测，但这种误差完全服从统计规律，对于同一物理量作多次的测量，随着测量次数的增加，随机误差的算术平均值趋近于零，因此多次测量的算术平均值将接近于真值。

（3）过失误差

由于操作错误或人为失误所产生的误差，这类误差往往表现为与正常值相差很大，在数据整理时应予以剔除。

4．实验数据的精确度

精确度（又称准确度）与误差的概念是相辅相成的，精确度高，误差就小；误差大，精确度就低。它反映系统误差和随机误差综合大小的程度。而测量中所得到的数据重复性的大小称为精密度，则反应了随机误差的大小，以打靶为例。图3-1表示弹着点密集而离靶心（真值）甚远，说明精密度高，随机误差小，但系统误差大；图3-1表示精密度低而正确度较高，即随机误差大，但系统误差较小；图3-1的系统误差与随机误差均小，精确度均高。

图3-1  精密度与精确度示意图