实验数据的处理方法

通过实验测得原始数据后需要进行计算将最终的实验结果归纳成经验公式或以图表的形式表示，以便与理论结果比较分析。因此由实验而获取的数据必须经过正确的处理和分析，只有正确的结论才能经得起检验。下面介绍这方面的基本知识。

一、有效数字与运算规律

二、实验数据的误差分析

三、实验数据处理

实验数据的处理就是将实验测得的一系列数据经过计算整理后用最适宜的方式表示出来，在化工原理实验中常用列表法、图示法和方程表示法三种形式表示。

1．列表法

将实验数据按自变量与因变量的对应关系而列出数据表格形式即为列表法，列表法具有制表容易、简单、紧凑、数据便于比较的优点，是标绘曲线和整理成为方程的基础。

实验数据可分为实验数据记录表（原始数据记录表）和实验数据整理表两类。

实验数据记录表是根据实验内容待测数据设计，如流体直管阻力测定实验的实验数据记录表格形式见表3-1

表3-1  流体直管阻力测定实验数据记录表

管子材料__________ 管子内径__________ 水的密度__________

水    温__________ 水的密度__________ 水的粘度__________

实验数据整理表是由实验数据经计算整理间接得出的表格形式，表达主要变量之间关系和实验的结论，见表3-2

表3-2  流体直管阻力测定实验数据整理表

根据实验内容设计拟定表格时应注意以下几个问题：

（1）表格设计要力求简明扼要，一目了然，便于阅读和使用。记录、计算项目满足实验要求。

（2）表头应列出变量名称、符号、单位。同时要层次清楚、顺序合理。

（3）表中的数据必须反映仪表的精度，应注意有效数字的位数。

（4）数字较大或较小时应采用科学记数法，例如可采用科学记数法记作，在名称栏中记为Re×10⁴，数据表中可记为2.5。

（5）数据整理时尽可能利用常数归纳法（即转化因子）。例如：计算固定管路中不同流速下的雷诺数时， 其中为定值。则可归纳为，常数即为转化因子乘以各不同的流速，即可得到一系列相应的，可减少重复计算。

（6）在数据整理表格下边，要求附以某一组数据进行计算示例，表明各项之间的关系，以便阅读或进行校核。

2．图示法

上述列表法一般难见数据的规律性，为了便于比较和简明直观地显示结果的规律性或变化趋势，常常需要将实验结果用图形表示出来，化工实验中正确作图的一些基本原则如下：

（1）坐标纸的选择

化工中常用的坐标有普通直角坐标、双对数坐标和半对数坐标，根据变量间的函数关系选择合适的坐标纸。

（a）直线关系：，选用普通直角坐标纸。

设一组实验数据变量间符合上述线性关系，方程中的截距a和斜率b见后一元方程的图解 。

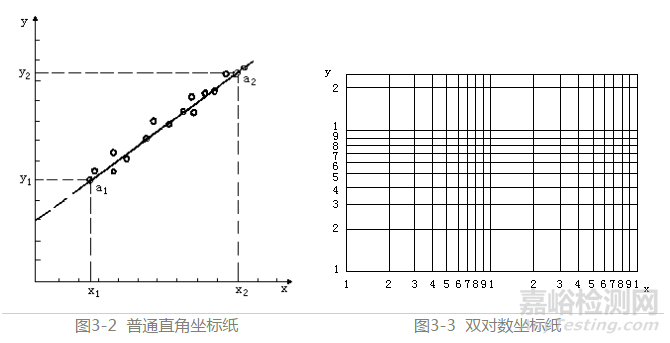
（b）双对数坐标纸

双对数坐标纸的横、纵坐标是以对数标度绘制而成，如图3-3所示。

1）对数坐标的特点

对数坐标的特点是：某点与原点的距离为该点表示量的对数值，但是该点标出的量是其本身的数值，例如对数坐标上标着5的一点至原点的距离是。如图3-4所示。

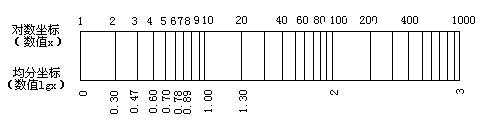
图3-4  对数坐标的特点

图3-4中上面一条线为x的对数刻度，而下面一条线为lgx的线性（均匀）刻度。对数坐标上1，10，100，1000之间的实际距离是相同的，因为上述各数相应的对数值为0，1，2，3，这在线性（均匀）坐标上的距离相同。

在对数坐标上的距离（用均匀刻度的尺来量）表示为数值之对数差，即lgx₁-lgx₂

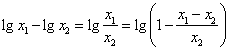
因此，在对数坐标纸上，任何实验点与图纸的直线距离（指均匀分度尺）相同，则各点与图线的相对误差相同。

在对数坐标纸上，一直线的斜率应为

由于与分别为纵坐标与横坐标上的距离与，所以可用尺量出直线上1，2两点之间的水平及垂直距离、，见图3-5 则斜率：

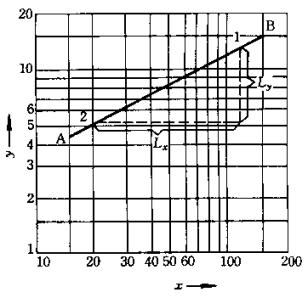
图3-5 双对数做标纸上直线斜率和截距的求法

2）选用双对数坐标纸的基本原则

（a）适用于幂函数，使非线性关系变换成线性关系。

幂函数在普通直角坐标上标绘是一条曲线，采用双对数坐标标绘可使之线性化，将上述幂函数等式两边取对数,则

令：    

则上式变换为,即为线性方程。

（b）适用于所研究的函数y和自变量x在数值上均变化了几个数量级。例如，已知x和y的数据为：

x=10，20，40，60，80，100，1000，2000，3000，4000

y= 2，14，40，60，80，100， 177， 181， 188，200

在直角坐标上作图几乎不可能描出在x的数值等于10，20，40，60，80时曲线开始部分的点（见图3-6），但是采用对数坐标则可以得到比较清楚的曲线（见图3-7）。

3）半对数坐标纸

半对数坐标纸的一个轴是分度均匀的普通坐标轴，另一个轴是分度不均匀的对数坐标轴，如图3-8所示。

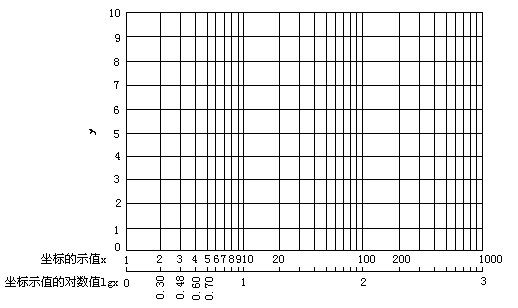
图3-8  半对数坐标纸

下列情况下可考虑用半对数坐标：

（a）变量之一在所研究的范围内发生几个数量级的变化

（b）在自变量由零开始逐渐增大的初始阶段，当自变量的少许变化引起因变量极大变化时，此时采用半对数坐标纸，曲线最大变化范围可伸长，使图形轮廓清楚。例如：用直角坐标纸做的图见图3-9，而改用半对数坐标纸后见图3-10。

（c）适用于指数函数，使其变换为直线函数关系。将上式等号两边取自然对数，则，所以与呈直线关系。

4）坐标的分度

坐标的分度指每条坐标轴所代表数值的大小，即选择适当的比例尺。

为了得到理想的图形，在已知量和的误差与的情况下，比例尺的取法应使实验“点”的边长为，，并且使，则

轴的比例尺为：

y轴的比例尺为：

如已知温度误差，则

温度的坐标分度为长，若感觉太大，可取此时的坐标为长。

5）坐标纸的使用及实验数据的标绘。

（a）按照使用习惯取横轴为自变量，纵轴为因变量，并标明各轴代表的名称、符号和单位。

（b）根据标绘数据的大小对坐标轴进行分度，所谓坐标轴分度就是选择坐标每刻度代表数值的大小。坐标轴的最小刻度表示出实验数据的有效数字，同时在刻度线上加注便于阅读的数字。

（c）坐标原点的选择，在一般的情况下，对普通直角坐标原点不一定从零开始，应视标绘数据的范围而定，可以选取最小数据将原点移到适当位置，对于对数坐标，坐标轴刻度是按1、2……10的对数值大小划分的，每刻度为真数值。当用坐标表示不同大小的数据时，其分度要遵循对数坐标规律，只可将各值乘以倍（取正负整数），而不能任意划分。因此，坐标轴的原点只能取对数坐标轴上规定的值做原点，而不能任意确定。

（d）标绘的图形占满整幅坐标纸，匀称居中，避免图形偏于一侧。

（f）标绘数据和曲线：将实验结果依自变量和因变量关系，逐点标绘在坐标纸上。若在同一张坐标纸上，同时标绘几组数据，则各实验点要用不同符号（如●，×，▲，○，◆等）加以区别，根据实验点的分布绘制一条光滑曲线，该曲线应通过实验点的密集区，使实验点尽可能接近该曲线，且均匀分布于曲线的两侧，个别偏离曲线较远的点应加以剔除。