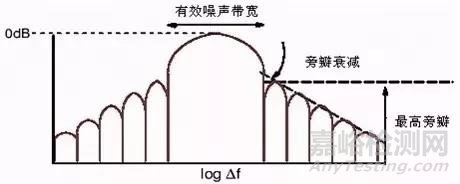
产生机理(边缘截断):
您当前的位置:检测资讯 > 科研开发
嘉峪检测网 2018-07-04 14:57
本文简单介绍了信号分析基础理论知识之频谱分析。
实际的波形可视为由若干正弦波所合成,每一正弦分量各有其一定的频率和幅值。
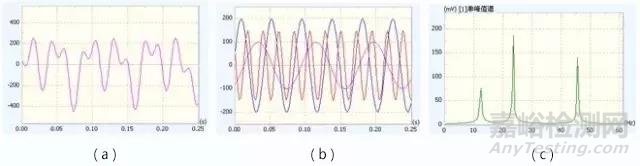
(a) 波形;(b) 由三个正弦波组成;(c) 频谱
(1) FT (连续傅里叶变换)
正变换:

逆变换:
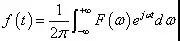
其中,ω=2πf,f(t)为时域数据序列,F(ω)为频域的谱函数序列。
(2) DFT(离散傅里叶变换)
对N个样点的数字化的时域波形进行数值积分计算,计算某一频率点的幅值。可在计算机上进行,但计算量巨大。
(3) FFT(快速傅里叶变换)
离散变换的一种快速算法,计算速度快,适合工程应用,但具有如下限制:
参与计算的数据点数(FFT分析点数)必须为2的幂次方,即2n。
频率分辨率问题,频率间隔Δf。

泄漏产生:当实际信号的频率处于f(i)和f(i+1)之间时,则会产生频率泄漏现象,导致误差。
频率误差:FFT频率反映的频率为(i-1)Δf Hz或者iΔf Hz,最大频率误差为Δf/2。
幅值误差:谱峰的幅值减小,泄漏到附近的谱峰上,最大幅值误差为36.3%。
整周期采样:信号的频率正好处于f(i)的位置上,即信号频率等于Δf 的整数倍,则不会产生泄漏。
产生机理(边缘截断):
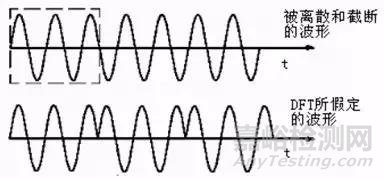
常用校正方法:
加窗处理:如hanning、平顶窗等,仅能校正幅值,不能校正频率;
频率计校正:可以对若干个单个谱峰进行校正,特点为快速实时,既能校正幅值,又能校正频率;
平滑处理:能有效校正最大谱峰处的幅值,不能校正频率。
加窗可消除或减轻信号截断和周期化带来的不连续问题。平滑是将频谱任何一点的附近若干点进行相加,将泄露到两边的能量加回来。
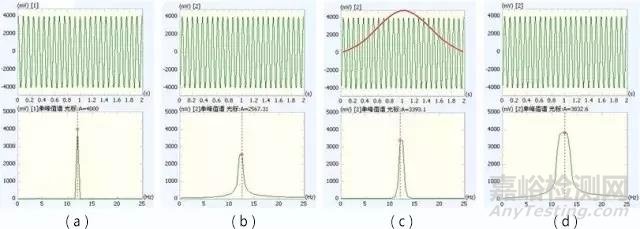
(a) 整周期;(b) 严重泄露;(c) 加汉宁窗;(d) 平滑
相当于滤波器。
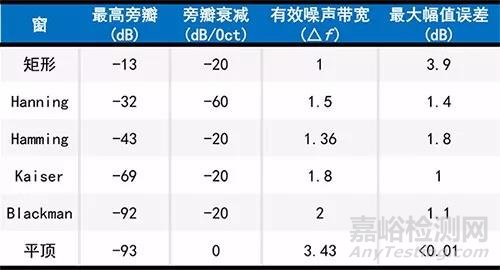

(a) 指数窗形式;(b) hanning窗形式;(c)hamming窗形式

(d) 平顶窗形式;(e) Kaiser窗形式;(f) 余弦矩形窗形式
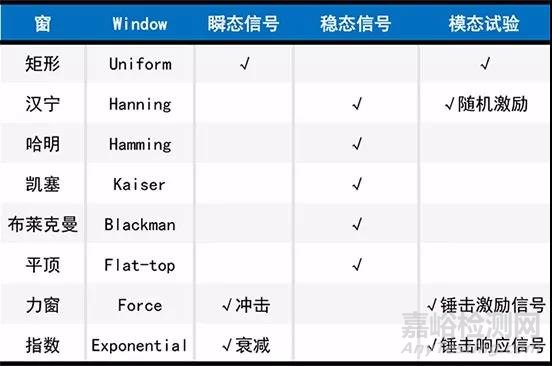
平均:
对较长的信号进行平均计算,用以消除随机噪声带来的误差。
一般有如下平均方式:
线性平均:全程分析过程中的每次FFT结果进行线性平均;
峰值保持:全程分析过程中,每条谱线分别保持其最大值,常用于扫频信号的分析;
最大值保持:全程分析过程中,搜索能量最大的一幅波形(总有效值最大),对其进行频谱分析,作为最后的结果;
指数平均:全程分析过程中的每次FFT结果进行指数平均,越后面分析的结果所占权重越大,最后一次占1/2,倒数第二次占1/4,依此类推。
重叠:
对于加窗处理,可充分利用其被窗函数衰减掉的部分的信号。
例如,从20Hz到160Hz的正弦匀速扫频信号,长度8K点,FFT点数1K点,hanning窗。

扫频信号无重叠加窗
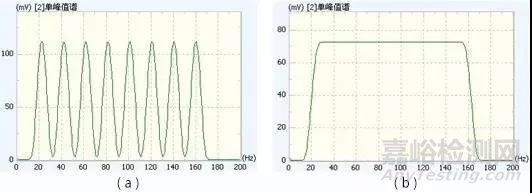
(a) Hanning,无重叠;(b) Hanning,90%重叠

来源:AnyTesting


