[摘要] 本文构造副车架静刚度与K&C 性能的并行仿真流程,提出考虑多学科性能耦合的副车架静刚度目标修正方法,并系统地建立一体式空心铸铝副车架分层级设计优化方法。首先,建立副车架计算模型并改进加载方法,提出局部坐标系下的静刚度计算方法,并集成副车架静刚度分析、模型缩减分析、K&C 性能分析3 种工况,执行多样本分析并通过实验设计矩阵转换,构建K&C 性能与静刚度性能的组合代理模型,基于组合代理模型利用K&C性能修正静刚度目标;其次,开展多性能约束的副车架多层级拓扑优化,通过第1 层级拓扑优化完成等壁厚主体结构设计,通过第2层级拓扑优化完成变壁厚结构设计。结果表明:经过多层级拓扑优化的副车架1阶、2阶扭转模态分别提升39.3%、14.9%,静刚度及K&C 性能满足目标要求,其他各项性能指标均得到显著提升且实现轻量化。本文可为副车架静刚度性能目标制定、K&C性能提升及副车架结构优化提供参考。
关键词:副车架;静刚度;K&C性能;拓扑优化;多性能约束
前言
副车架是连接车身与悬架系统的关键部件,其结构设计要满足多学科性能,关于副车架设计优化方法一直是研究的热点[1-3]。文献[4]中以副车架动刚度为性能指标,采用尺寸优化和形状优化为技术手段,发现达成动刚度指标至少需要增质量15%,说明在架构不变的情况下,仅通过调整厚度和形状来大幅提升性能会付出较大代价,有必要优先开展拓扑优化改善整体架构设计;朱剑峰等[5]以后副车架硬点刚度为性能约束开展拓扑优化,以硬点刚度、结构模态为性能优化指标开展参数设计,对钣金副车架设计具有重要参考价值;马芳武等[6]重点考虑典型载荷工况,采用折衷规划法进行副车架拓扑优化,并建立参数化模型对后副车架进行多目标优化,可以支撑概念阶段钣金副车架结构参数化设计。廖莺等[7]进一步完善拓扑优化阶段的工况定义,并提出后副车架目标制定方法,经过拓扑优化和多学科优化,轻量化效果显著,但拓扑概念设计阶段要求强度这一局部性能达标,可能出现过设计问题,副车架刚度目标制定采用经验方法无法准确兼顾K&C 性能。林佳武等[8]从碰撞性出发,通过拓扑优化实现真空高压铸铝后纵梁结构轻量化,由于工艺特征和成型方法差异较大,高压铸造车身部件的优化方法不适用于低压铸造的底盘部件。
新能源汽车对高性能和轻量化的极致追求,促进集成度更高的一体式空心铸铝副车架的推广和应用,基于上述研究的局限性,本文提出考虑性能耦合的副车架静刚度目标修正方法,并系统性地建立一体式空心铸铝副车架分层级设计优化方法。首先,建立副车架模型并定义局部坐标系下的静刚度计算方法,并根据K&C 性能指标修正静刚度性能目标,为副车架多学科性能优化打下科学的基础;其次,基于模态和静刚度等全局性能开展拓扑优化设计主体结构,进而通过局部区域加强完成变壁厚设计;经过多层级拓扑优化可以在满足各学科性能要求、同时实现副车架最大限度的轻量化。
1 、 副车架静刚度计算方法
1.1 计算模型及边界条件
副车架作为电动汽车多级隔振的重要一级,概念设计各硬点及名称如图1 所示,其与车身往往通过悬置柔性连接。以图2 所示的副车架前、后悬置点为例阐述柔性连接建模方法:创建两个串联的零长度CBUSH 单元,一个用于模拟车身安装点刚度,另一个用于模拟副车架悬置刚度,并约束车身端耦合点1~6 自由度。为便于编程,前上控制臂简写为FUCA,前下控制板简写为FLCA,后上控制臂简写为RUCA,后下控制臂简写为RLCA,前束臂简写为SCA。

图1 副车架基准有限元模型及硬点示意图

图2 副车架与车身柔性连接建模示意图
1.2 加载及静刚度计算方法
现有分析方法采用在悬架控制臂内侧硬点位置分别沿着整车坐标系 X、Y、Z 方向进行加载[7],这无法准确关联静刚度与关注的行驶性能运动特征。悬架控制臂运动受力方向与整车坐标系坐标轴往往存在一定夹角,为更准确表征控制臂运动及受力特征,基于局部坐标系进行分析加载和测量,局部坐标系定义如下:控制臂的轴向定义为局部坐标系Y 向,为主方向,控制臂衬套轴向为X 向,局部坐标系的Z 向可根据右手定则获取且方向朝上。加载定义:沿着局部坐标系X、Y、Z向加载1 000 N载荷。
按照上述静刚度计算新方法,对约束状态的副车架进行两次刚度分析,第1 次对柔性副车架分析,刚度记为Ktotal;第2 次分析刚性副车架(在柔性副车架基础上将材料弹性模量放大1 000 倍等效),刚度记为Krigid。综合两次刚度分析结果,通过消除副车架与车身柔性连接的影响,定义副车架静刚度K。
式中:Ktotal = F/Uflex;Krigid = F/Urigid;Uflex、Urigid 分别为柔性副车架模型、刚性体副车架模型同一加载点的位移。
2 、 基于K&C性能的静刚度目标修正
本文建立融合多学科工况的仿真流程,见图3。基于同一有限元模型结构参数,打通静刚度性能与运动学K&C 性能两个学科之间的关联关系。将尚未建立车身柔性连接的副车架作为基准有限元模型(参考图1),对副车架与车身的连接进行等效,建立副车架约束模型,进行静刚度分析;将副车架基准有限元模型、各控制臂有限元模型转化为超单元模型,进一步地,基于超单元模型建立高精度K&C 模型并进行仿真分析。可以实现副车架静刚度分析、超单元模型缩减分析、K&C 性能分析3 种工况的并行仿真分析,并能自驱动多样本迭代计算。
图3 静刚度与K&C的并行仿真流程示意图
其中,高精度刚柔混合模型构建及K&C 仿真分析方法如下:采用Craig-Bampton[9-10]将副车架、控制臂、转向节等有限元模型缩减为MNF 格式超单元模型;基于Adams软件输入各弹性部件各方向刚度、阻尼等连接信息,结合MNF 模型建立运动学关系,完成悬架K&C 特性分析模型建立,规避了传统简化建模方法无法准确得到副车架等部件刚度、惯量参数的弊端;进一步地,编制批处理命令调用Adams对高精度分析模型自动求解,并将仿真结果转化为可编辑的文本文件格式。
2.1 执行实验设计
根据悬架硬点和布置空间,借助一体式空心铸铝副车架的概念设计数据(见图1),采用本文提出的加载和计算方法完成静刚度分析,采用高精度刚柔混合模型完成K&C 仿真分析。以副车架每个特征面厚度为设计变量(对称面设定共用一个设计变量),参考工艺能力定义设计变量范围为4~9 mm,利用最优拉丁超立方设计的方法完成200 个样本点的生成,得到设计变量与静刚度性能、K&C 性能的实验设计矩阵表,如表1所示。
表1 实验设计矩阵表
2.2 构造性能间的组合代理模型
代理模型的一般数学模型可表示如下[11]:

式中:f(x)为真实模型;f̂(x)为代理模型;ε(x)为近似误差。
单一代理模型无法对所有优化问题都有较强的预测能力[12],而组合代理模型具有更稳定的近似能力[13]。一般而言,预测精度越高对应的单一代理模型权系数越大,本文选取精度较高的单一代理模型参与组合代理模型构造,利用预测平方和(prediction sum of squares,PRESS)误差评价准则计算权重系数,建立PWS 组合代理模型(PRESS weighted surrogate, PWS):

式中:m为参与构造组合代理模型f̂EN(x)的单一代理
式中:Ek 表示第k 个单一模型的预测平方和;Eavg 表示所有单一模型的预测平方和均值;经过试验[14],推荐参数值α = 0.05,β = -1。
代理模型常用来逼近设计变量与性能指标之间的真实映射关系,而本文研究的重点是静刚度性能与K&C 性能之间的关系,进一步对表1 的实验设计矩阵进行转换,将静刚度性能指标转换为设计变量,K&C 性能作为性能指标。根据全局误差评估指标R2(R2 越接近1 精度越高),从12 种常用代理模型中选出精度较大的PRSM、RBF、Kriging 模型构造组合代理模型Ensemble。精度对比结果见表2(其中LTC、LTC-a 分别为侧向力、反侧向力柔度),组合代理模型综合近似能力相对更优。
表2 代理模型精度对比
结合具体车型K&C 性能开发需求,在悬架硬点设计冻结前提下,筛选、识别需要通过副车架提升的K&C 性能,筛选原则:(1)不满足目标值要求的K&C性能;(2)与副车架刚度相关性较为显著的K&C 性能。识别结果:加速前束柔度(ACC toe compliance,ATC)尚未满足性能目标[-0.02,-0.005]下限要求,且与副车架刚度相关性较为显著(相关性系数>0.4);制动前束柔度(brake boe compliance, BTC)、侧向力前束柔度(leteral toe compliance, LTC);反向侧向力前束柔度(letaral toe compliance anti, LTC-a)与副车架刚度相关性较为显著,但性能均符合目标要求;故以ATC 为重点优化对象,其他K&C 性能作为性能约束。
基于Spearman 相关性系数统计结果见表3,发现5个控制臂中的后下控制臂Y向刚度(RLCA_ty)和后上控制臂Y 向刚度(RUCA_ty)对ATC 性能影响较为显著,基于组合代理模型提取显著设计变量与关注性能的映射关系见图4,可以预测,增加后下控制臂Y 向、后上控制臂Y 向静刚度,能够提升前束加速俯仰性能。
表3 K&C性能与静刚度的相关系数
图4 显著设计变量与关注性能映射关系图
2.3 静刚度目标修正
本文结合性能指标特征,采用自适应差分进化算法(self-adaptive differential evolution,SaDE),以副车架静刚度RLCA_ty、RUCA_ty 为设计变量,以K&C 性能为约束和优化目标进行求解,其表达式如下:
式中:pi 为K&C 特性中第i 个性能;piL、piH 分别为第i个性能要求的上下限值;ti 为第i 个性能的目标值,对于ATC性能取目标值的中位数;twi为权重系数。
优化迭代历程的气泡图见图5,可以发现,为满足所有K&C 性能需求,需要重点提升RLCA_ty、RUCA_ty两个性能(蓝色样本为可行方案)。由图5也可以看出,后下控制臂Y 向刚度的上限值较后上控制臂Y 向刚度上限值高33%,且后下控制臂附近存在底部加强梁结构,性能提升潜力更大,综合副车架的初始结构设计的静刚度和K&C 性能关联的结果对静刚度经验值进行目标修正,见表4,后上、后下控制臂Y 向静刚度值需要提升不低于13.6%、31.8%。
表4 控制臂主方向静刚度性能目标修正


图5 优化迭代气泡图
3 、 副车架结构多层级拓扑优化
静动态多工况拓扑优化设计多采用建立综合目标函数并确定子目标权重系数的折衷规划法,本质上是将多目标优化问题转化为单目标优化问题[15]。针对各工况性能目标明确的优化,将多工况性能目标优化问题转化为以多工况性能目标为约束、最小化拓扑域体积分数的优化问题[16],可获得较为准确的结构路径。本文结合一体式空心铸铝副车架的工艺特征,提出基于多性能约束的多层级拓扑优化方法,见图6,其中V(X)表示体积分数,gi(X)表示第i个工况的性能,本文约束工况gi(X)包括静刚度、模态、动刚度性能,cl为性能目标下限值,ch为性能目标上限值。
图6 基于多性能约束的多层级拓扑优化方法
多层级设计优化思路为:第1 层级拓扑以概念可行设计空间X1 为优化对象,识别关键传力路径,完成壁厚为T1 的副车架设计;第2 层级拓扑,在第1层级设计基础上,在内壁区域增加设计空间X2,对应的厚度为T2,以设计空间X2 为优化对象,识别对性能灵敏度区域,完成变壁厚具体结构设计。其中,T1为工艺可行的最小厚度值,T1+T2为工艺可行的最大厚度值。
拓扑优化采用SIMP方法,拓扑域 X 被离散为一定数量的单元,将密度作为设计变量赋予每个单元,利用数学规划法决定单元密度,1 表示有材料,0 表示材料完全删除,材料插值模型表达如下[17]:

式中:Ei 为第i 个单元插值后的弹性模量;E0、Emin 分别为单元初始定义的弹性模量和最小弹性模量;ρi为第 i 个单元的相对密度,ρi ∈[0,1]; p 为惩罚因子。本文定义实体单元惩罚因子p = 3,Emin/E0 =0.01。
3.1 第1层级拓扑优化
拓扑域X1 定义为整体设计空间减去悬架运动包络区域及相关件(电驱系统、车身底护板、车身纵梁等)布置区域后的概念可行设计空间。拓扑域X1划分为实体网格,开展第1 层级多模型拓扑优化,拓扑优化结果如图7。
图7 第1层级拓扑优化1/2截面图示意
根据拓扑优化结果设计副车架主体结构框架,设计原则定义如下:(1)根据拓扑结果的关键传力路径(单元密度接近1 的单元),解读副车架各区域的截面特征及过渡设计,确定副车架主体结构;(2)副车架初始壁厚统一采用工艺可实施的最小厚度。基于拓扑结果完成等壁厚副车架的初次设计,见图8,已具备副车架工程设计的雏形,相较于图1 的概念设计方案,优化后的副车架下横梁沿+X 向后移,且与副车架主体呈一体化铸造成型,后下控制臂接附点嵌入加强梁端部,对后下控制臂位置静刚度提升更为直接。

图8 等壁厚设计方案示意图
3.2 第2层级拓扑优化
副车架初次工程设计方案采用工艺可实施最小厚度,此时图8 的等壁厚结构设计方案未能充分体现图7 拓扑优化的理想效果。对图8 的设计数据进行仿真分析,发现模态及部分刚度性能尚未达标,为满足所有性能需求,有必要进一步借助拓扑优化识别性能灵敏的结构区域,通过对灵敏区域加强设计,形成变厚度方案。将副车架初次设计方案作为非设计域,在梁系内侧构造的封闭空间定义为拓扑域X2,进行第2层级拓扑优化,优化结果如图9所示。
图9 第2层级拓扑优化1/2截面图示意
可以发现:与第1 层级优化特征不同,第2 层级拓扑优化的特征是局部区域材料聚集,说明此区域对性能灵敏度较高,需要在空心梁壁对应区域的内侧或外侧加强,改进为变壁厚的再次设计方案,并对方案进行性能验证。本文副车架前横梁中部区域对性能最灵敏,高灵敏度区域的单元密度也均接近1,同时为降低工艺难度,将图9 中材料聚集区域均匀增加壁厚,前横梁底部区域变厚度设计如图10 所示,最大厚度和最小厚度之间的过渡区采用倒角平滑过渡,最大厚度采用工艺可行最大厚度6 mm,最小厚度采用工艺可行最小厚度4 mm,副车架结构、厚度为左右对称设计。
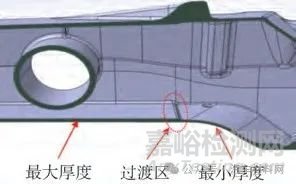
图10 变壁厚设计方案示意图
3.3 副车架优化方案验证
参考第2 层级拓扑优化结果,对副车架进行工程化设计,仿真验证发现静态工况、模态工况、动刚度工况等相关全局性能全部达标,与概念设计方案性能对比见表5。
表5 关键性能对比
对比结构设计演变过程和性能变化可以发现:拓扑优化方案的各项性能指标均得到显著提升并减质量0.7 kg;2阶扭转模态是目标体系下副车架结构的决定因素,优化后性能分别提升39.3%、14.9%,达成模态指标需要强化副车架前横梁结构设计,而电机前悬置点等效静刚度远超目标值说明其对前横梁设计影响较小;同时,第1 层级拓扑优化使下横梁后移,后下控制臂内嵌于下横梁端头的设计,也促进后下控制臂Y向性能大幅提升。
将副车架工程化方案有限元模型超单元转化执行K&C 特性分析,见表6。由表可见:K&C 各性能,特别是与副车架刚度相关性较为显著的各项性能均满足目标;ATC 性能得到改善,由不达标转化为满足目标要求。这也在一定程度上说明根据K&C 性能对静刚度目标修正,并通过优化静刚度改善K&C性能的方法是有效的。
表6 与副车架刚度显著相关的K&C性能对比
4 、 结论
(1)本文改进静刚度加载方法,提出局部坐标系下的静刚度计算新方法,基于有限元模型结构参数,打通静刚度性能与运动学K&C 性能两个学科之间的关系。基于组合代理模型,挖掘静刚度性能与K&C 性能之间的耦合关联规律,修正静刚度性能目标,可为工程中K&C 性能提升及副车架静刚度性能指标制定提供参考。
(2)提出铸铝副车架多层级设计优化思路,并进行副车架多层级拓扑优化,开展第1 层级拓扑优化完成等壁厚主体结构设计,开展第2 层级拓扑优化加强局部区域完成变壁厚工程化设计。结果表明,优化副车架在满足多学科全局性能指标的同时实现轻量化,静刚度及关联的K&C 性能满足目标,模态性能大幅提升。
参考文献
[ 1 ] FAN W, YIN L, XU Z, et al.Two-stage surrogate-based optimization of a vehicle composite subframe with modified fast flexible space-filling designs[J].Mechanics of Advanced Materials and Structures, 2023, 30(4):724-737.
[ 2 ] NAM J S, SHIN H W, CHOI G J.Durability prediction for automobile aluminum front subframe using nonlinear models in virtual test simulations [J].International Journal of Automotive Technology, 2014, 15(4):593-601.
[ 3 ] MENG X, SUN Y, HE J, et al.Multi-objective lightweight optimization design of the aluminum alloy front subframe of a vehicle[J].Metals, 2023, 13(4):705.
[ 4 ] OUYANG T, WU J, CHEN Q, et al.Multi-objective combination optimization of automobile subframe dynamic stiffness[C].SAE Paper 2023-01-0005.
[ 5 ] 朱剑峰, 王水莹, 林逸, 等.后副车架拓扑优化概念设计和智能轻量化方法研究[J].汽车工程, 2015, 37(12):1471-1476.ZHU Jianfeng, WANG Shuiying, LIN Yi, et al.A study on the methods of concept design with topology optimization and intelligent lightweighting for rear subframe[J].Automotive Engineering, 2015, 37(12):1471-1476.
[ 6 ] 马芳武, 王卓君, 杨猛, 等.汽车后副车架轻量化概念设计方法研究[J].汽车工程, 2021, 43(5):776-783.MA F W, WANG Z J, YANG M, et al.Research on lightweight conceptual design method of vehicle rear subframe[J].Automotive Engineering, 2021, 43(5):776-783.
[ 7 ] 廖莺,李峰,李志.概念设计阶段铝合金后副车架轻量化设计[J].汽车工程,2020, 42(12):1737-1743.LIAO Y, LI F, LI Z.Lightweight design of aluminum rear subframe in conceptual design stage [J].Automotive Engineering,2020, 42(12):1737-1743.
[ 8 ] 林佳武, 李玄霜, 陈宗明, 等.真空高压铸造铝合金车身后纵梁轻量化设计[J].汽车工程, 2020, 42(3):383-389.LIN J W, LI X S, CHEN Z M, et al.Lightweight design of body rear longitudinal beam of VAHP die-casting aluminum alloy[J].Automotive Engineering, 2020, 42(3):383-389.
[ 9 ] WU L , TISO P , KEULEN F V.Interface reduction with multilevel craig–bampton substructuring for component mode synthesis[J].AIAA Journal, 2018, 56(5):1-15.
[ 10 ]PRADEEPKUMAR S , NAGARAJ P.Dynamic substructuring method for vibration analysis of complex structures[J].Journal of Vibration Engineering & Technologies, 2022(1):10.
[ 11 ]龙腾,刘建,WANG G Gary,等.基于计算试验设计与代理模型的飞行器近似优化策略探讨[J].机械工程学报,2016,52(14):79-105.LONG T, LIU J, WANG G Gary, et al.Discuss on approximate optimization strategies using design of computer experiments and metamodels for flight vehicle design[J].Journal of Mechanical Engineering, 2016, 52(14):79-105.
[ 12 ]童水光, 何顺, 童哲铭, 等.基于组合近似模型的轻量化设计方法[J].中国机械工程, 2020, 31(11):1337.TONG S G, HE S, TONG Z M, et al.Lightweight design method based on combined approximation model [J].China Mechanical Engineering, 2020, 31(11):1337.
[ 13 ]VIANA F A C, HAFTKA R T, STEFFEN V.Multiple surrogates:how cross-validation errors can help us to obtain the best predictor[J].Structural and Multidisciplinary Optimization,2009, 39(4):439-457.
[ 14 ]GOEL T, HAFTKA R T, SHYY W, et al.Ensemble of surrogates [J].Structural and Multidisciplinary Optimization, 2007,33(3):199-216.
[ 15 ]张志飞, 陈仁, 徐中明,等.面向多目标的汽车悬架控制臂拓扑优化研究[J].机械工程学报, 2017, 53(4):114-121.ZHANG Z F, CHEN R, XU Z M, et al.Research on multi-objective topology optimization of vehicle suspension control arm [J].Journal of Mechanical Engineering, 2017, 53(4):114-121.
[ 16 ]占金青, 彭怡平, 刘敏, 等.基于多性能约束的连续体结构拓扑优化设计[J].计算机集成制造系统, 2022, 28(6):1746-1754.ZHAN J Q, PENG Y P, LIU M, et al.Topology optimization of continuum structures with multiple performance constraints [J].Computer Integrated Manufacturing Systems, 2022, 28(6):1746-1754.
[ 17 ]廉睿超, 敬石开, 李营, 等.考虑最小尺寸精确控制的SIMP和MMC 混合拓扑优化方法[J].力学学报, 2022, 54(12):3524-3537.LIAN R C, JING S K, LI Y, et al.A hybrid topology optimization method of SIMP and MMC considering precise control of minimum size[J].Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(12):3524-3537.

























