与球面相比，非球面因为具有更多的面型自由度，一片非球面镜便可达到多片球面镜组成的透镜组的效果，可以极大地减小光学系统的尺寸和质量，提高系统的成像质量，甚至可以达到衍射极限，在现代光学系统中应用的越来越广泛。但是因为其高自由度的面型，高精度的非球面面形检测一直是光学检测领域的一大难题。

干涉法作为非球面最终的加工检测方法，具有灵敏度高、测量准确度高、可实现非接触测量等优点，是非球面高精度面形误差检测的重要方法，应用十分广泛。干涉测量法根据测量原理分为零位检验法与非零位检验法。

零位检验法的基本思想[1]是，当被测镜为理想非球面且检测系统理想装调时，测试光束经过被测镜后能够原路返回，与参考光束发生干涉后产生“均匀一片色”的零条纹或等间距直条纹。而当被测镜是理想非球面镜时，按照零位条件，为了使测试光束经被测非球面后能够原路返回，需要在检测系统中使用特殊的补偿光学元件，使干涉仪出射的平面波或球面波转换成与被测理想非球面面形一致的非球面波，以补偿被测非球面像差。在检测实际的非球面时，根据实际干涉条纹与理想干涉条纹之间的偏差，可以得到被测非球面的面形误差。

零位检验法具有很高的检测精度，但零补偿器往往结构比较复杂，加工制造成本高难度大，且针对性很强，一种补偿器只能用于一种特定参数的非球面面形误差的检测，通用性不强。

与零位检验法相比，非零位检验方法使用的补偿器部分补偿非球面的像差，补偿器结构比较简单，非零位检验法对补偿系统的光学设计要求有所下降，但对系统的机械装调控制、检测算法等提出更高的要求。本文将介绍部分补偿法、拼接测量法、双波长全息法以及倾斜波干涉法。

1   部分补偿法

部分补偿法[2]是一种新的非球面检测技术，与零补偿法不同，部分补偿法不要求补偿器完全补偿待测非球面的像差，允许补偿后检测系统像面处存在一定的剩余波前，只要控制该剩余波前像差在一定的范围内，使其引起的干涉条纹密度不超出探测器的分辨范围即可。

本节介绍一种应用部分补偿原理与数字莫尔移相技术[3]的非球面面形误差检测方案，检测原理如图1所示[4]。利用改进的泰曼格林干涉仪，搭建实际测量系统，采集经部分补偿器补偿后CCD探测到的一幅实际干涉图。在光学设计软件中搭建虚拟干涉仪，其中待测样品为与待测非球面对应的理想非球面，代入部分补偿镜的结构参数，通过光线追迹得到虚拟系统理论干涉图。利用数字移相的方法，通过理论干涉图生成相位差依次为π/2的四幅移相虚拟干涉图。利用莫尔合成技术，将一幅实际干涉图分别与四幅虚拟干涉图相乘，得到四幅莫尔合成干涉图。通过对莫尔干涉图进行相位解算可以求解出非球面的面形误差信息。

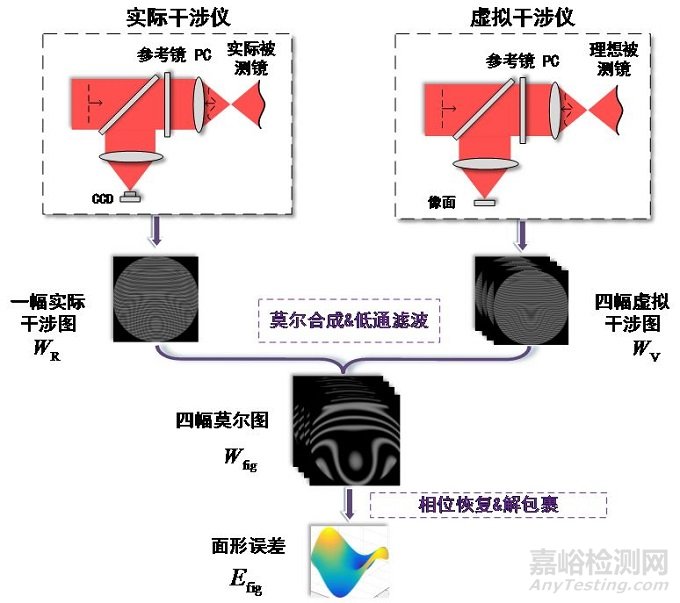
图1 检测原理示意图

数字移相技术的引入能够省去传统机械移相装置的使用，精简系统机构，避免误差源的引入，提高干涉测量系统的稳定性。虚拟干涉仪的引入使得检测系统能够通过单帧实际干涉图完成非球面的检测，为非球面面形误差的瞬态检测提供了可能。而莫尔合成技术的引入，将虚拟干涉图与实际干涉图联系起来，实现了虚拟标准参考面与实际被测面之间的相干。

如图2所示为用于凸非球面检测的部分补偿实例示意图[5]。光路中使用折反式部分补偿器。干涉仪出射的平行光经透射式透镜L1会聚后，穿过球面反射镜M1的中心开口入射到待测凸非球面M2上，经M2反射到达M1后原路返回到M2，光线第二次被M2反射后，沿入射时的传播路径原路返回，通过M1中心开口后经透镜L1后回到干涉仪中。

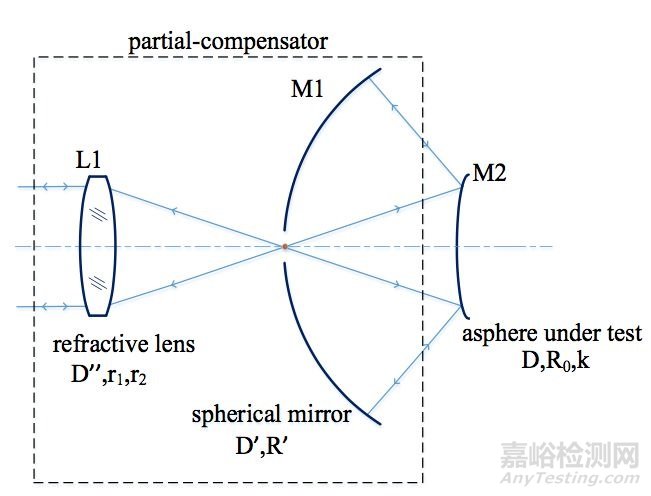
图2 折反式部分补偿器

该折反式部分补偿器有以下优点：首先，球面反射镜的使用易于实现光线的会聚，且相比较于完全使用折射式光学元件的补偿器，反射镜的引入，可降低折射式透镜折射率均匀性引入的误差，易于加工，精度更高；其次，折反式光路结构避免了折射系透镜组补偿系统长焦距、大孔径的缺点，使得非球面的检测系统结构更加简单紧凑。

相对于零补偿法而言，由于检测系统允许一定量的剩余波前像差存在，部分补偿法法降低了补偿器设计和加工的难度，并且可以用一种部分补偿器对多种参数的非球面进行测量，用尽可能少的补偿器实现尽可能多的补偿，提高了测量的通用性[6]。

2   拼接测量法

拼接测量法的思想是“总-分-总”，即将非球面面形分成若干个局部区域，通过将局部区域的准确结果通过图像拼接生成非球面整体面形结果。根据局部区域的形状又可以分为环带拼接法与子孔径拼接法。

2.1   环带拼接法

环带拼接法是指，在旋转对称非球面的检测中，当待测非球面沿着光轴运动到某一位置时，干涉图上会出现少量可分辨的环状干涉条纹，如图3所示。为了得到非球面的完整检测结果，将待测非球面置于干涉仪光轴方向上的多个位置，通过多个位置环状条纹的“拼接”，实现整个非球面的检测。

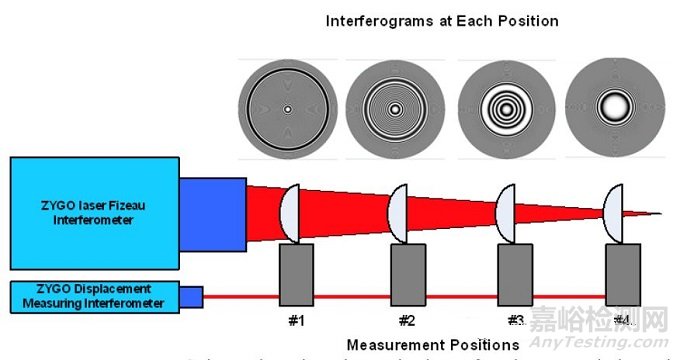
图3 环带拼接法测量原理

环带拼接法的优点是测量原理简单，但要实现环状条纹的准确拼接，需要准确测量待检非球面的位置，因此在检测装置中往往需要高精度的位移测量装置。

2.2   子孔径拼接法

子孔径拼接法[7]是将待测非球面口径划分成若干个子孔径进行测量。根据子孔径形状的不同，常见的子孔径拼接法有环形子孔径拼接法、圆形子孔径拼接法和矩形子孔径拼接法等。如图4所示为椭圆子孔径拼接算法各个子孔径的干涉图样与待测非球面全口径相位恢复结果[8]。通过图像处理算法与子孔径拼接算法将各个子孔径的测量结果拼接可以得到非球面完整的面形误差测量数据。

图4 椭圆子孔径拼接法相位恢复结果

子孔径拼接法的优点是不需要借助辅助光学元件（如补偿镜），能实现大口径、大非球面度非球面全口径面形误差的测量，检测精度高，很好的解决了高分辨率与大视场之间的矛盾。但子孔径拼接法的算法复杂且耗时，无法用于大口径非球面面形误差的实时检测，检测装置的装调与校准存在一定的难度。

3   双波长全息法

双波长全息法的原理[9]是采用两种不同波长光源进行非球面面形误差测量，得到两幅携带非球面面形误差的干涉图。通过合成算法求解出两种波长的等效合成波长，相当于用一个波长较长的光源进行非球面面形误差的检测。由于干涉仪产生的干涉图条纹间距在一定程度上会依赖于干涉仪光源的波长，干涉仪光源波长越长，干涉条纹越稀疏。因此，双波长全息法能够避免数值解包裹算法误差的引入，即使待测非球面表面梯度很大时，双波长相位解包裹得到的相位分布精度仍然高于传统数值解包裹算法。

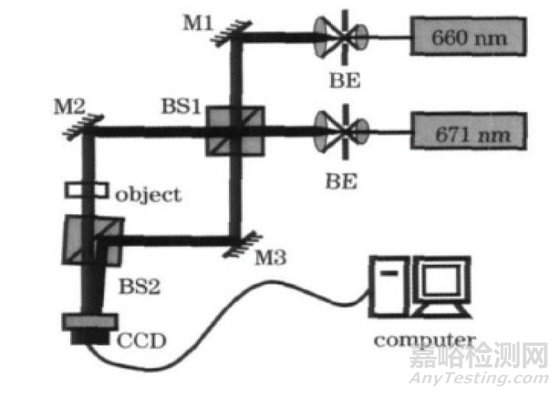
图5 双波长数字全息三维成像装置示意图

如图5所示为双波长数字全息三维成像装置示意图。波长为660nm的激光光源入射到分光镜BS1，被分为两束，一束被反射镜M1反射到达分光镜BS2作为参考光束，另一束被反射镜M2反射后通过被测物体到达分光镜BS2作为测试光束。参考光束与测试光束在分光镜BS2处发生干涉并被记录成一幅数字全息图。波长为671nm的激光传输路径与第一种波长激光传输路径一致，参考光束与测试光束发生干涉被记录成另一幅数字全息图。两幅图像相乘得到的合成图像包含的相位信息分布与等效合成波长通过检测系统生成的干涉图样相同。通过相位解算，便能求解出待测非球面的面形误差。

4   倾斜波干涉法

倾斜波干涉仪[10]（TWI）是在泰曼格林干涉仪的基础上改进而来的。与泰曼格林干涉仪的不同之处：①在光路中的傅立叶平面上放置光阑，以限制探测器处探测到的条纹密度；②装置中采用位于准直系统焦平面上的二维点光源阵列进行照明，可以使得测试光束到达被测面时携带不同倾斜波。

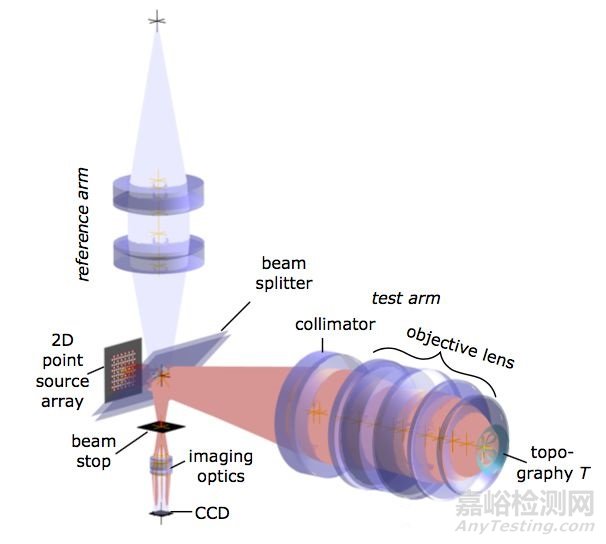
图6 倾斜波干涉仪原理装置图

如图6所示[11]，二维点源阵列发出的光经过分光棱镜后被分成两束光，其中一束为参考光束，另一束为测试光束。在测试光路中，二维点源阵列发出的多束入射光，经过准直透镜组后产生多束具有不同倾角的球面波，因此可以认为二维点源阵列的使用在测试光路中引入了球面波点源阵列。多重倾斜球面波入射到待测样品上，对待测样品的局部区域进行梯度补偿，然后经待测样品反射回来的携带有待测样品面形偏差的倾斜波面再次经过准直镜组后入射到分光棱镜上，在分光棱镜处与参考波面发生干涉，经成像透镜后形成干涉图被CCD接收。通过对获得的干涉图进行解算、重构将待测样品的面形信息恢复出来。

在非球面非零位的干涉检测中，非球面上任意一点的实际法线与非球面最佳拟合球面上该点的法线之间存在偏转角，这就导致入射光经过待测非球面后无法原路返回。此时测试波面与参考波面发生干涉时可能会由于测试波前倾角过大，导致干涉条纹过密，CCD无法分辨。而倾斜波面干涉法是在检测系统中引入一个二维点光源阵列，产生多束具有不同倾角的入射波前，从而对被测非球面上各点的实际法线与最接近比较球面法线之间的偏转角进行补偿，以保证CCD可以探测到可分辨的干涉条纹。

5   总结与展望

随着光学技术的不断发展，精密光学系统对非球面光学元件的需求日益增加，非球面高精度定量检测技术成为先进光学制造领域的前沿课题。本文调研了国内外非球面检测技术的研究现状和发展趋势，基于不同的测试原理，把现有的非球面检测方法归纳为零检验法与非零检验法，并对每种检验方法的特点进行了分析。

非球面的检测技术还需进行进一步的探索以期实现基于单幅干涉图的非球面面形误差瞬态检测，以及在实际测量中，使用结构简单，测量效率高，且抗振效果好的检测装置。