摘要 作为设备稳定服役能力的一种衡量,可靠性对工程技术发展和创新十分重要。基于物理、信息论和统计方法的耦合,可靠性研究正逐步发展并有望成为一门新的科学。同时随着量子技术的发展,量子相干器件及设备将会被大量地植入到传统装备系统中。这不仅给可靠性自身的研究带来新的机遇和挑战,也会使量子物理和可靠性研究交叉起来,导致交叉领域思想上的原始创新。文章首先介绍可靠性研究从工程向科学迈进的历程,然后从可靠性工程需求的视角介绍量子可靠性的基本概念和逻辑,强调量子自洽历史对寿命统计的内在描述,最后结合目前量子技术所面临的退相干挑战,展望可靠性工程对量子技术的潜在应用。
关键词 可靠性理论,浴盆曲线,最大熵原理,退相干历史,量子可靠性
1、引 言
可靠性是工程技术领域中的重要概念,具体是指一个产品或设备在规定的条件下和规定的时间内,完成规定功能的能力。这一概念大约是在上世纪二三十年代提出的,几乎与量子力学同时诞生并同步发展。一战后,工业生产能力的迅猛增长推动全球经济的复苏,同时也促进了可靠性工程技术的不断进步。二战期间,飞机等武器装备开始大量使用电子元件,受限于当时的技术,电子元件工作十分不稳定,电子设备的可靠性问题十分突出,这促使此后美国有组织地开展对电子设备的可靠性研究;另一方面,德国在火箭的研制中,首次引入从部件到系统的整体可靠性分析思路,即通过部件可靠性相乘累加的方式估计系统的可靠性。二战结束后,可靠性在工程技术科学基础研究方面引起了更多科学家的关注。例如,因为早期单个电子元件的可靠度普遍较低,无法组成足够高可靠度的系统,著名数学家冯‧诺伊曼(Von Neumann)为此提出了一个解决思路[1]:利用多个不那么可靠的组件,通过结构冗余的方式组成可靠度较高的装备系统[2]。该思路逐步发展形成了今天人们研究可靠性的一般逻辑方法[3]。自60年代起,以各国国家意志主导的重大工程(如载人航天、战略武器研制和延寿等)极大推动了相关可靠性理论和方法的发展。
时至今日,可靠性分析不仅逐步从工程技术走向科学研究,而且成为战略装备安全服役定量化决策的基础。随着可靠性分析方法在工程应用领域发挥重要作用,可靠性研究逐步得到完善并发展成为了一个独特的研究领域。需要指出的是,由于很多人对可靠性的认知还停留在服务于工程技术的应用层面,最近关于可靠性工程是否成为一门新科学的问题引起了学界的激烈争论。争论的焦点之一是关于描述部件或系统退化过程的浴盆曲线(它是可靠性工程核心概念中的一个)能否从第一原理推导出来。在大多数系统中,系统的失效率曲线呈现浴盆状,P. Rocchi认为浴盆曲线是普适性的统计规律,可靠性有可能发展成为一门新科学[4]。然而,存在一些不满足浴盆曲线的例子,例如果蝇的死亡率是倒置浴盆曲线[5]。由于人们不能从原理出发推导出系统失效的浴盆曲线,这个争论一直延续至今。
过去的可靠性研究大多是从工程实际需求出发,根据具体问题进行建模。要想将其提升为一门科学,则必须从原理出发,分析不同问题之间的内在逻辑和共性问题,从基础上形成一套统一的理论框架和实验验证方法。以上提到的研究基本上是从统计学的角度出发,唯象地探讨浴盆曲线的由来。进一步的研究有必要从物理相关的基本原理出发,研究系统的可靠性结构及其时间演化问题。
在分析系统可靠性时,系统的可靠性逻辑结构往往起到关键作用。一个系统可以分为多个部件,每个部件又可以再细分为多个子部件,每个部件的失效和退化都在不同程度上决定了系统的退化行为。当系统不断细分为子系统和部件,达到细观或微观尺度时,系统的失效机理必将受到量子效应的影响,因此可靠性的最终基础在一定程度上可以归结为量子物理。
其实,在可靠性的观念被广泛地应用于相关工程技术领域的同时,量子力学的飞跃式发展也先后催生了核能、半导体和激光等科技创新。而今,随着量子计算和量子信息等量子技术的不断进步,量子相干器件在计算、通信、感知和安全等各个领域的巨大潜力引发了人们广泛的关注,量子器件构成的量子装备(如量子计算机)有可能在不久的将来走向应用。然而,如何确保量子相干器件的长期稳定运行并发挥其不可替代的技术功能,成为了新一代量子工程技术发展必须面对的重大科学问题。对于这类微观部件组成的系统,其可靠性的衡量将受到诸多来自量子力学的限制。对于宏观的系统而言,可靠与否的区分不存在任何原理上的限制,但是对于利用量子态实现功能的器件而言,可靠与否的区分必须是相对于正交态而言的。另外,可靠程度的量化实际上是一个过程依赖的量,而系统状态演化轨迹之间的量子干涉往往会使得过程依赖物理量的统计性质,无法用经典概率论描述。同时,状态间的相干叠加如何影响可靠性也是一个挑战性的科学问题。由于这些限制和挑战的存在,我们必须对量子器件或者植入量子部件的可靠性进行原理性分析。
本文首先简要介绍可靠性研究,扼要阐述浴盆曲线假设和结构函数理论,并结合目前退相干问题对前沿量子技术提出的挑战,在没有波包约化的量子力学数学框架下引出量子可靠性的概念,并阐述其探索的科学意义。本文同时面向物理和工程背景的读者,介绍可靠性工程中与统计物理、量子物理等物理学领域相联系的概念和内容。笔者希望以此让物理背景的读者更多地了解可靠性工程、更多地参与其科学研究,同时也希望为可靠性工程提供新的研究视角,以在可靠性科学基础上有所突破。
2、退化过程的浴盆曲线研究及其“第一原理”
每一个装备或器件都有自己的寿命。针对特定功能而言,个体间存在的固有差异导致同类器件的寿命出现随机性,并服从某个分布。因此,人们通常采用概率测度来度量可靠的程度,即可靠度可以定义为系统保持时间t内不失效的概率(也叫存活函数或可靠度函数),记为R(t),其中t即为系统的寿命。在此基础上,可以定义失效率函数(风险函数)x(t) ≡ -(dR/dt)/R,它表示存活概率的相对变化率。需要指出的是,失效率函数是可靠性工程中的核心概念之一[4],它的刻画和描述不应当只停留在工程技术层面上。人们通过失效率函数曲线的形状就能判断和预测出系统失效风险随着时间的变化情况。在可靠性工程发展初期,系统的可靠度和风险函数通常需要根据大量的寿命数据运用统计学方法来获得。然而,在实际应用场景中,由于各类限制,系统寿命相关的数据量可能极为有限,甚至无法获取。这些现实困难驱使人们根据经验并结合唯象假设来分析可靠度。其中最为著名的唯象假设是以下将介绍的浴盆曲线。
在工程领域中,对各类系统的长期统计结果表明,有相当一部分设备(尤其是电子设备)的失效率曲线在三个不同的使用时期呈现出三种变化趋势,如图1所示[6]:第I阶段时,早期系统处于磨合阶段,有较高的失效风险,经历磨合之后系统失效风险下降;第II阶段为平稳期,过了平稳期后,系统全寿命周期即将结束;转入第III阶段后,失效率又重新回升,系统将很快走向死亡。这类失效率曲线被命名为浴盆曲线。由于这一现象符合人们的经验常识,并且在大量的设备器件中也观察到了浴盆曲线,因此人们有理由相信浴盆曲线可能是普适的。
图1 浴盆曲线示意图(图片来自文献[6](重画))
人类记载的浴盆曲线最早并不是在近代的可靠性工程领域内,而是17世纪Breslau城市的人口死亡率统计[7]。当时婴儿夭折的概率较高导致了前期高死亡风险,到了后期由于衰老导致抵御疾病的能力下降使死亡率再次升高。1969年,Gnedenko等人在他们的著作[6]中首次把浴盆曲线引入到可靠性工程领域,他们发现大量的实验数据显示失效率曲线x(t)会呈现出浴盆的形状。当然,他们也指出这一结论并非完全普适:随着产品质量把持能力的提升以及筛查流程的加入,一些元件没有早期高失效率的阶段。时至今日,关于浴盆曲线的争论一直存在。这些争论的焦点是浴盆曲线的普适性。支持的一方认为浴盆曲线是一种理想条件下普适的失效率曲线[4]。反对方则批评浴盆曲线缺乏理论根据[8—10]。
人们曾经提出各类概率模型来刻画浴盆曲线以及其他形状的失效曲线。其中一种典型的构造方法是对常见的分布函数做概率混合[11],或者是将各个不同的失效率做混合。这类混合的含义是指一个系统会经历不同的失效模式。具体来说,早期高失效风险是因为存在先天缺陷的系统,它们与正常系统的失效风险并不相同,在任务开始时的磨合期,有缺陷的系统会快速失效,而正常系统则会平稳地度过这段时期。但是这仍然无法解释后期高失效风险的行为。
通过统计数据建立失效率曲线的方法实质上是一种统计推断,作为统计推断方法之一的最大熵原理正是统计力学的逻辑基础。最近,本文作者(杜,孙,关)及其合作者,一起研究了最大熵原理在失效率推断方面的理论和应用[12]。我们的研究动机是,能否基于原理给出失效率函数所满足的运动方程,并给出浴盆曲线。在研究中,我们利用最大熵原理得到了任意约束条件下的运动方程(Box 1中的方程(3))。根据运动方程的解,列举了出现浴盆曲线的约束条件及其取值范围。特别地,把寿命统计的一阶矩和二阶矩作为约束条件,且当它们的取值在一定范围内时,推断出的失效率曲线就是浴盆曲线。除此之外,对于其他的实际中观察到的失效率曲线类型,例如,单调型、倒置浴盆型等,利用这一方法均能在适当的条件下给出,如图2所示。事实上,该理论提供了从实际观测数据到失效率曲线的一种较为普适的方法。后来,我们也将该理论推广到了具有多组寿命参数的多组件可靠性问题中[13]。
图2 最大熵原理得到的各类失效曲线示意图,其中绿色曲线为浴盆曲线,β1、β2为最大熵约束中的参数[12]
以上研究都是在系统层次上进行的研究,并未仔细考虑系统的内部结构。如果从物理上解释其普适性,需要从部件失效引起系统失效的具体过程出发进行建模研究,这是物理学“还原论”的观点。然而,如果每一个部件都是e指数退化的,系统的退化怎么会表现为浴盆曲线?不过从“演生论”的观点看,一个包含大量自由度的系统,其集体行为与个体行为中的大部分细节无关。如果从这个角度理解浴盆曲线普适性,一个自然的问题就是:在怎样的系统中,系统失效率随时间演化的趋势与各个部件演化趋势中的细节几乎无关?这个现象与多体物理学中的演生现象非常相似。以下将从结构函数复杂性的角度出发介绍一种理解其普适性的模型[17]。
BOX 1
最大熵原理与失效率推断
首先考虑一个离散随机变量X,它有不同的取值,记为x1, x2, ⋯, xi, ⋯。第i个取值pi出现的概率为pi。这样p ≡ (p1, p2, ⋯)就是一个随机分布,它满足概率归一化条件 。对于分布函数p,香农(C. E. Shannon)熵定义为
。对于分布函数p,香农(C. E. Shannon)熵定义为
它刻画随机事件不确定性的大小。类似地,对于连续随机变量Y(取值记为y),可以对熵的形式稍作推广:
假设已知该分布的某些平均值, 。这个等式和归一化条件一样可以看作是关于分布p必须满足的约束条件。然而,同时满足这些条件的分布并不唯一。统计推断的任务之一便是在这些满足约束条件的分布集里选择出一个或一些相对合理的分布函数。最大熵原理的基本思想是选择这些满足约束条件的分布中熵最大的那个分布,即认为系统处于不确定性最大的分布上。
。这个等式和归一化条件一样可以看作是关于分布p必须满足的约束条件。然而,同时满足这些条件的分布并不唯一。统计推断的任务之一便是在这些满足约束条件的分布集里选择出一个或一些相对合理的分布函数。最大熵原理的基本思想是选择这些满足约束条件的分布中熵最大的那个分布,即认为系统处于不确定性最大的分布上。
根据最大熵原理的假设,可以通过计算得到给定约束下的“最优”分布,
其中α和β1, β2,⋯是拉格朗日乘子分别对应归一化约束和关联期望值的约束。上述方程的解即为“最优”分布p*,

其中 。参数βk由方程组
。参数βk由方程组 确定。例如y是相空间坐标,f(y)是系统哈密顿量,那么分布p*(y)就是正则系综。
确定。例如y是相空间坐标,f(y)是系统哈密顿量,那么分布p*(y)就是正则系综。
1957年,E. T. Jaynes首先指出最大熵原理是统计物理的逻辑基础[14—16]。Jaynes把这一信息论的思想应用到统计物理基础的研究,他认为统计力学不是“力学”,而是已知部分信息(如平均能量)对另一部分“力学量”期望值(如动量)的统计推断。这个工作不仅使得人们从信息论的视角理解统计物理,而且对统计学有深远的影响。当只有一个能量平均值的约束 时,我们得到正则分布:
时,我们得到正则分布:
其中 。
。
最大熵原理可以用于系统寿命分布的推断,寿命的概率密度函数是p(t)≡-dR/dt=x exp(-X),其中 。可以把熵和约束看为作用量,即(x,X)的泛函,
。可以把熵和约束看为作用量,即(x,X)的泛函,
变分得到欧拉—拉格朗日方程:
例如取寿命的一二阶矩作为约束条件:f1(t)=t,f2(t)=t2,就可以得到不同趋势的失效率曲线,包括单调递增、浴盆型和倒置浴盆型,这些曲线都是实际系统中常见的。
3、结构函数复杂性与普适失效行为的涌现
根据前文所述,可以通过部件冗余来提升系统整体的可靠度。这一思路的引入对可靠性工程产生了重要的影响[3],具体为以下两个方面:一方面是从系统设计角度,可以通过不同的冗余方式来优化设计系统的可靠度;另一方面从可靠性评估的角度,系统的可靠度可以通过部件的可靠度来确定。系统与部件之间的状态依赖关系称为结构函数[18],它描述了怎样的部件状态能够使系统的功能得以实现,也体现了部件性能的冗余程度。例如,把系统状态与部件状态都粗略地分为可靠或不可靠两种(第i个部件状态记为σi=1,0),那么对于一个包含N个部件的系统而言,它的结构函数是包含N个自变量的递增布尔函数Σ=ϕ(σ1,σ2,⋯,σN),函数取值代表系统的状态Σ。由于利用部件的可靠性状态得到系统整体的可靠性状态的过程是将多个自由度合并成一个自由度,因此实质上这是一种粗粒化,也代表了某种冗余度。
当系统的部件数目足够庞大时,结构函数的复杂性可能会使得系统的失效规律(如失效率时间演化趋势)不能再简单地用部件的失效规律来描写。这可以理解为复杂系统中的演生现象。关于演生现象,物理学家P. W. Anderson曾有一句著名的论述:“多者异也(more is different)”[19],即当系统包含大量组件时,组件之间的相互作用或者系统的组织方式将导致系统整体的行为有别于单个组件的行为。例如,虽然超导体中包含大量电子,但是超导现象却不能由独立电子的行为描述;再如,每个水分子H2O结构是一样的,但由它们组成的雪花却千姿百态,呈现不同的正六边形结构,与H2O本身结构没有直接联系。我们的研究发现,对于复杂系统可靠性的问题,系统的失效规律是由粗粒化过程的不动点性质决定的,而不再由单个部件失效风险的时间变化趋势决定。
事实上,包含数量庞大部件的复杂系统通常具有多层次的特征。这里多层次特征是指一个系统包含若干个子系统,而子系统又可以进一步向下分解并以此类推直至最基础的部件。系统的失效过程是从基础部件开始的,然后逐步向上传递直至系统层。对于相邻两层之间可靠度的依赖关系由结构函数确定。系统的状态可以由基础部件状态出发通过一系列结构函数的复合作用后给出。
Box 2分析了结构函数的性质,对于只有一个阈值的情形,当部件可靠度高于该阈值时,由于每一层结构都起到保护作用,随着层数的增多,系统变得越来越可靠,反之则越来越不可靠。
BOX 2
不动点与系统可靠性
考虑每个部件的状态是统计独立且相同的,根据结构函数,我们可以用部件可靠度r 计算系统的可靠度R,即用一个多项式函数来描写:R=fϕ(r)≡〈ϕ(σ1,σ2,⋯,σN)〉,其中〈⋯〉代表对σ1,σ2,⋯,σN的系综取平均。当所有部件都可靠时,系统一定是可靠的,fϕ(1)=1,反之,当所有部件都不可靠时,系统一定不可靠fϕ(0)=0。可以看出这两个点是不动点。除了这两个不动点,fϕ一般还具有第三个不动点rϕ,0≤rϕ≤1,可以证明对于任意ϕ,当rϕ≤r≤1时,R≥fϕ(r);当0≤r≤rϕ时,R≤fϕ(r)。这个不动点给出了部件可靠度的阈值,当部件可靠度大于该阈值时,系统的可靠度高于部件,此时系统的结构对系统起到保护性作用,系统失效被延缓。与之相反,当部件可靠度低于阈值时,系统失效一定被加速。
当含有不同阈值的多个结构函数经过适当概率混合后,阈值的数目可以发生变化。即除了r=0和r=1外,fϕmix可具有多个不动点。如图3(b)所示,fϕmix(r)在0<r<1之间具有两个不动点r1和r2(r1>r2),系统在r1<r<1范围内加速失效,在r2<r<r1范围内保持稳定,在0<r<r2范围再次加速失效,于是系统整体出现浴盆曲线。
对于复杂系统中部件可靠度高于阈值时,底层部件失效向上层传递受阻的这一现象,从统计物理的角度看是一种渗流[20]。对于这类系统,部件开始缓慢失效的初期,系统的失效风险十分低,当系统接近阈值时,失效风险陡然增加。在层数足够多时,系统失效率函数的趋势与部件失效率函数的细节几乎无关。例如考虑部件的可靠度用威布尔分布r(t)=exp(-tα)刻画,它对应的部件失效率是αtα-1,当0<α<1时,部件失效率随时间递减,当α>1时,部件失效率随时间递增。因此参数α可视为描写部件个体退化行为细节的参数。如果系统结构函数只有一个不动点(图3(a)),当系统层数足够大时,系统层次的失效率x(t)呈现单调递增变化(图3(c))。对比图3(c)的左右两小图可以看出,在层数L足够大时,不同的α取值不会影响系统失效率的变化趋势。这表明系统失效行为不依赖于部件细节。此时可以认为,系统层次涌现出了与部件不同的失效行为:它不再简单地由部件失效率的演化趋势决定,而是由结构函数的性质决定。
图3 (a)和(b)展示相邻两层子系统的可靠度关系示意图,根据Box 2中的分析,图中蓝色曲线与黄色直线的交点即为不动点。图(a)中的fϕ(r)在0<r<1范围内有一个不动点,图(b)中的fϕ(r)在该范围内有两个不动点,对应图中的r1和r2。假设部件寿命是威布尔分布r(t)=exp(-tα)(这里时间t已被无量纲处理),它对应的部件失效率是αtα-1,当0<α<1时,部件失效率随时间递减,当α>1时,部件失效率随时间递增。(c)和(d)展示多层系统的失效率时间变化趋势。其中图(c)中每一层结构对应于(a),这类结构函数在r(t)小于不动点时,会抑制系统失效风险。从(c)中可以看出,随着层数L的增加,系统早期失效率受抑制效果变得显著。当层数足够多时,系统失效率呈递增趋势,这一趋势不依赖于部件层次的细节参数α。图(d)中每一层结构对应于(b),这种结构函数在r2<r(t)<r1范围内,会抑制系统失效风险,在此范围以外,会增加系统失效风险。因此如图(d)中当层数足够多时,无论部件失效率递增(α=1.1)还是递减(α=0.7),系统的失效率曲线都是浴盆曲线[18]
然而,上述得到的失效率并非浴盆曲线。浴盆曲线中存在两个失效率随时间快速转变的阶段,即早期高风险进入平稳期,以及平稳期进入末期高风险。如果这样的行为也是结构函数导致的,那么对应的fϕ应当具有两个非稳定的不动点(图3(b))。系统的失效率如图3(d)所示,对比图3(d)的两个小图可以看出,当系统层数足够大时,系统层次的失效率都是浴盆曲线,同样改变部件细节参数α也不会影响这一特征。复杂系统结构函数的不确定[21],一方面可以被视作失效模式混合的一种起源,另一方面也为理解浴盆曲线普适性提供了一种解释。
4、量子可靠性及其“历史”
主观性是影响可靠性工程的要素之一,原因是失效的判断标准通常来自于人们的经验。这些判据大多是考察系统特征物理参数是否在某个区域范围,有时它可以表述为系统物理状态空间的某些限制。从前面关于多层级系统的问题中可以看出,对于系统可靠与否的判断是最为粗粒化的。随着层次的下降,要对各层次的各个子系统做可靠与否的判断,这其实是对系统物理状态做更为精细的区分与判断。因此对于一些更精细的系统,随着在细观或微观尺度上量子效应的出现,这种主观性判断进一步向更深层次渗透。
图4 两波包重叠(不正交),从系综统计的意义上,如果波包中心位置间距离的尺度不小于波包宽度的尺度,那么这两个波包可以被区分。从单次观测的意义上,不论波包中心位置间距离的尺度是否大于波包宽度的尺度,只要两个波函数不正交,则它们无法确定地被区分
根据量子力学的基本观点,物体的运动呈现波动性,而物质波在空间中的延展特征会对运动状态的区分带来一定限制。如图4所示,对于两个交叠的波包能否被区分,从经典的视角看,如果波包中心位置间距离的尺度不小于波包宽度的尺度,那么这两个波包可以被区分。但这里值得注意的是,无论是波包中心位置还是宽度都是统计结果。实验中想要获得统计结果,必须事先制备出系综。由于不可克隆定理[22],用统一的方法制备任意未知量子态的系综是不可能的,并且如果两个波包有交叠,那么无法通过单次测量的读数确定性地区分它们,这是因为总有一定的概率出现交叠处的读数。两个没有交叠的波包在希尔伯特空间中总是正交的,因此非正交态不可区分[22]。从这个意义上讲,如果要确定性地区分一个量子系统可靠与否,那么失效判据必须定义在一组正交态之上,即可靠状态和非可靠状态对应的希尔伯特子空间是正交的。这可以看作是量子力学和可靠性在小子样(指样本数不足)前提下共同作用的结果。因此,在微观上区分可靠与否是一个内在的挑战。
此外,如前所述,一个系统的可靠性定义为系统在规定时间内保持功能的能力,这可以通过系统保持可靠状态的概率来刻画。经典可靠性定义依赖于系统状态的演化过程,它的量子版本对应于量子历史过程。在量子力学中,系统不同演化轨迹历史之间的干涉,过程量往往无法用经典的语言和逻辑描述,这是量子可靠性研究的另一个挑战。所幸,R. B. Griffiths在上世纪80年代提出的量子力学自洽历史诠释[23,24]给出了如何描述量子过程及其和经典描述之间的关系。为了更好地介绍量子可靠性,Box 3简要回顾自洽历史诠释。
BOX 3
自洽历史诠释
量子系统的历史指的是系统在希尔伯特空间随时间发展演化的轨迹,它包括了时间演化和测量操作。例如,一个粒子从t0时刻在x0位置出发,t1时刻处在x1位置,t2时刻处在x2位置,…,一直到tn时刻在xn位置,这就是一段历史。可以把多条不同的历史看成一个整体形成粗粒化的历史,如图5所示。
在更一般的意义下,历史中每个时刻所经历的状态可以用希尔伯特子空间的投影算符E0, E1, E2, ⋯来描述。根据量子力学的自洽历史诠释,某一特定时刻ti,系统是否可靠由投影算符Ei来刻画,若系统态|ψ〉处在该投影算符的子空间内,即Ei|ψ〉=|ψ〉,称系统可靠。同样,系统不可靠对应的投影为Ei⊥(Ei⊥≡I-Ei),系统演化将在可靠与可靠之间形成一条轨迹,即历史,如:可靠、可靠、可靠、不可靠这一历史对应的就是E0, E1, E2, E3⊥。通常不同历史之间是相互干涉的,我们无法对每一个历史路径独立定义概率。但是,可以根据系统的演化算符U(t, t')对每一段历史定义权重,W(E0, E1, ⋯, En)≡Tr(ρ0hh†),其中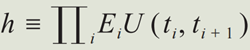 。这个权重在某些情况下不能解释为概率,此时,我们称这组历史不自洽。自洽历史理论对不同历史之间的自洽性给出了精确的定义,它可以表述为:如果任意多条历史的权重之和都等于这些历史粗粒化后的权重,那么这些历史是自洽的。例如,一个粒子从t0时刻在x0位置出发,ti时刻处在xi或xi′位置,一直到tn时刻处在xn位置是一段粗粒化的历史,它的权重需要满足以下条件才是自洽的:
。这个权重在某些情况下不能解释为概率,此时,我们称这组历史不自洽。自洽历史理论对不同历史之间的自洽性给出了精确的定义,它可以表述为:如果任意多条历史的权重之和都等于这些历史粗粒化后的权重,那么这些历史是自洽的。例如,一个粒子从t0时刻在x0位置出发,ti时刻处在xi或xi′位置,一直到tn时刻处在xn位置是一段粗粒化的历史,它的权重需要满足以下条件才是自洽的:
当历史是自洽的,历史权重就满足概率测度的基本要求,权重就变成了几率。此时如果从这些已经自洽的历史角度考察系统的演化过程,可以认为这段过程是经典的。
对于不自洽的历史,可以引入测量仪器和系统之间的适当耦合,使得系统和仪器的整体的历史变得自洽,即利用量子仪器参与的量子测量把原本不自洽的历史权重变成概率。在这个描述中,仪器必须由量子力学描述,测量不能简单地假设为波包塌缩。例如,在图6的电子双缝干涉实验中,对电子经过的窄缝进行观测时干涉条纹消失的这一现象可以被解释为,测量仪器的加入使得电子上下两条路径对应的历史满足自洽条件,此时仪器和系统整体的历史之间不再相互干涉。这种经典概率分布的涌现意味着量子系统真实状态的时间演化特性是客观存在的。
图5 一个粒子从t0时刻处在x0位置出发,经过不同路径在tn时刻处在xn位置。左图和右图分别代表细粒化和粗粒化的路径
图6 粒子通过不同的双缝将经历不同的“历史”,如A-B-C’-D(红色路径)或A-B’-C-D(蓝色路径),它们是相干的
基于自洽历史理论,我们研究了量子相干器件可靠性的描述问题[25],提出了量子可靠性的新概念。首先根据自洽历史理论为每一条历史分配了相应的权重,此时权重暂时不能代表概率。然后,通过引入基于量子仪器的测量,使得包含仪器和系统的整体的细粒化历史满足自洽条件,历史轨迹间彼此独立,以上赋予的权重就变成了器件量子可靠性的概率测度。在这个框架下,量子器件描述方式与经典可靠性的刻画十分相似,由此可以得到量子部件可靠性分析中的寿命分布和失效率曲线等。同时,这类权重量化了实际过程和理想过程之间的差别,并可在不同历史颗粒度下进行分级,因而可以视为量子细粒化的过程保真度。
我们的工作还给出了量子系统结构函数的明确描述方式。在量子系统内部,量子部件状态之间的量子纠缠是经典系统内经典部件所没有的独特特征,这一特征也会改变系统的结构函数,进而影响系统可靠性。例如,用三比特翻转码保护的量子存储:三个物理比特即为系统的三个部件,所保护的逻辑比特是系统的整体状态。当储存的逻辑比特是无相干性的态时,系统的结构函数是经典可靠性中常见的一种,即如果三个部件有两个以上可靠,那么系统可靠。而当储存的逻辑比特是叠加态时,需要在物理比特之间引入纠缠。此时,系统的结构函数无法再用经典可靠性理论描写。图7绘制了系统可靠度(RL)与部件可靠度(RP)的依赖关系,可以看出,当改变系统初始状态即部件之间的纠缠时,阈值(曲线和对角线的交点)会发生相应的改变。这表明部件之间量子纠缠会改变系统结构函数进而影响阈值的大小。其中,越小的阈值表示这种冗余结构对系统的保护越好,当阈值等于1的时候这种冗余结构完全无法保护系统。
图7 三比特翻转码保护的逻辑比特可靠性RL和物理比特可靠性RP关系图。其中被保护的逻辑比特状态是 ,曲线与对角线的交点代表部件可靠性阈值[25]
,曲线与对角线的交点代表部件可靠性阈值[25]
近年,量子计算的技术奇点备受瞩目。量子可靠性可以为定量讨论技术奇点问题提供帮助。技术奇点是指,当某项技术积累到某个水平后,后续的发展将得到极大的加速以至于颠覆当下人们的认识和理解。近年,以量子计算、量子传感、量子通信为代表的量子信息技术快速发展。其中量子计算正孕育着颠覆传统计算技术的潜力,它的技术突破备受关注。目前量子信息技术所面临的主要挑战之一是量子态退相干问题。为了实现通用量子计算,人们采取纠错编码的方式保护量子比特的信息。其中表面码是一种受广泛关注并被寄予厚望的编码方式[26]。人们根据容错阈值判断表面码是否起到保护效果。这里的容错阈值指的是物理比特错误概率的临界值,当物理比特错误概率低于某个临界值时,逻辑比特发生错误的概率随码距的增加而降低。这里码距可以视为衡量错误冗余程度的特征量。最近,国内外的研究团队相继在实验上观察到了逻辑比特错误概率随码距增加而降低的现象[27—29]。这些结果被认为是量子计算研究已出现接近技术奇点的曙光。
从可靠性理论的视角看,容错阈值事实上是前文中系统与部件关系阈值的推广,它描写不同冗余结构稳定性之间的关系,而且和前文中阈值一样是由结构函数和噪声模型共同决定的。量子可靠性理论还可以处理一般的噪声模型以及相关的含时问题,因此有望为这些阈值问题突破提供一些新的思考角度和计算方法。
5、总 结
近年,关于可靠性是否为一门新科学的话题引起了广泛的关注和争论。我们从物理的角度,分析该领域中的几个受关注问题,并希望以此探索这些可靠性工程问题背后的科学基础。本文首先从传统可靠性的浴盆曲线讲起,通过统计推断给出浴盆曲线的推导,同时研究了多层级结构下系统层面失效率的涌现行为。随着系统逐步细化到量子层面,引出量子可靠性概念,分析了可靠性理论与量子力学相结合所需满足的基本限制,并展望了可靠性理论在量子技术领域的潜在应用价值。在量子技术发展的驱动下,不久的将来,量子物理与可靠性工程势必交汇融合,逐步成为交叉科学的新前沿领域。与此同时,面对这些新的机遇和挑战,从可靠性工程中建立一门兼具广泛且统一的可靠性科学,其重要性再次突显。但是,由于关于可靠性是否为一门新科学的争论尚未停止,因此本文的视角难免受到作者知识和兴趣偏好的影响。最后需要指出,本文介绍的内容(包括我们自己的工作)只是可靠性科学探索的“盲人摸象”,离可靠性科学的最后建立还是有相当的距离。本文旨在抛砖引玉,期望引发可靠性研究和物理学领域间的学术交流和融合,在奠定可靠性工程科学基础、形成可靠性科学的同时,面向实际需求,在重大工程技术上有所创新突破。
参考文献
[1] Neumann J V. Probabilistic Logics and the Synthesis of Reliable Organisms from Unreliable Components. Princeton:Princeton University Press,1956
[2] Moore E F,Shannon C E. J. Franklin Inst.,1956,262:191
[3] Mine H. IRE Trans. Circuit Theory,1959,6:138
[4] Rocchi P. Reliability is a New Science. Berlin:Springer International Publishing,2017
[5] Carey J R,Liedo P,Orozco D et al. Science,1992,258:5081
[6] Gnedenko B V,Belyayev Yu K,Solovyev A D. Mathematical Methods of Reliability Theory. Academic Press,1969
[7] Halley E. Philos. Trans. R. Soc. London,1693,17:596
[8] Klutke G A,Kiessler P C,Wortman M A. IEEE T. Relib.,2003,52:125
[9] Wong K L. Qual. Reliab. Eng. Int.,1988,4:279
[10] Gaonkar A,Patil R B,Kyeong S et al. IEEE Access,2021,9:10282
[11] Kunitz H. IEEE T. Reliab.,1987,38:351
[12] Du Y M et al. Phys. Rev. E,2020,101:012106
[13] Du Y M,Chen J F,Guan X F et al. Entropy,2021,23:348
[14] Jaynes E T. Phys. Rev.,1956,106:620
[15] Jaynes E T. Phys. Rev.,1957,108:171
[16] Jaynes E T. Proc. IEEE,1982,70:939
[17] Du Y M,Sun C P. Reliab. Eng. Syst. Safe.,2022,228:108756
[18] Barlow R E,Proschan F. Mathematical Theory of Reliability. Society for Industrial and Applied Mathematics,1996
[19] Anderson P W. Science,1972,177:4047
[20] Stauffer D,Aharony A. Introduction to Percolation Theory. Taylor & Francis,2003
[21] Cui L X,Du Y M,Sun C P. Reliab. Eng. Syst. Safe.,2023,234:109146
[22] Nielsen M A,Chuang I L. Quantum Computation and Quantum Information. Cambridge:Cambridge University Press,2000
[23] Griffiths R B. J. Stat. Phys.,1984,36:219
[24] Griffiths R B. Consistent Quantum Theory. New York:Cambridge University Press,2001
[25] Cui L X,Du Y M,Sun C P. Phys. Rev. Lett.,2023,131:160203
[26] Fowler A G et al. Phys. Rev. A,2012,86:032324
[27] Zhao Y et al. Phys. Rev. Lett.,2022,129:030501
[28]Google Quantum AI. Nature,2023,614:676
[29] Bluvstein D,Evered S J,Geim A A et al. Nature,2024,626:58



 。对于分布函数p,香农(C. E. Shannon)熵定义为
。对于分布函数p,香农(C. E. Shannon)熵定义为


 。这个等式和归一化条件一样可以看作是关于分布p必须满足的约束条件。然而,同时满足这些条件的分布并不唯一。统计推断的任务之一便是在这些满足约束条件的分布集里选择出一个或一些相对合理的分布函数。最大熵原理的基本思想是选择这些满足约束条件的分布中熵最大的那个分布,即认为系统处于不确定性最大的分布上。
。这个等式和归一化条件一样可以看作是关于分布p必须满足的约束条件。然而,同时满足这些条件的分布并不唯一。统计推断的任务之一便是在这些满足约束条件的分布集里选择出一个或一些相对合理的分布函数。最大熵原理的基本思想是选择这些满足约束条件的分布中熵最大的那个分布,即认为系统处于不确定性最大的分布上。

 。参数βk由方程组
。参数βk由方程组 确定。例如y是相空间坐标,f(y)是系统哈密顿量,那么分布p*(y)就是正则系综。
确定。例如y是相空间坐标,f(y)是系统哈密顿量,那么分布p*(y)就是正则系综。 时,我们得到正则分布:
时,我们得到正则分布:
 。
。 。可以把熵和约束看为作用量,即(x,X)的泛函,
。可以把熵和约束看为作用量,即(x,X)的泛函,



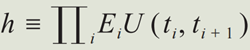 。这个权重在某些情况下不能解释为概率,此时,我们称这组历史不自洽。自洽历史理论对不同历史之间的自洽性给出了精确的定义,它可以表述为:如果任意多条历史的权重之和都等于这些历史粗粒化后的权重,那么这些历史是自洽的。例如,一个粒子从t0时刻在x0位置出发,ti时刻处在xi或xi′位置,一直到tn时刻处在xn位置是一段粗粒化的历史,它的权重需要满足以下条件才是自洽的:
。这个权重在某些情况下不能解释为概率,此时,我们称这组历史不自洽。自洽历史理论对不同历史之间的自洽性给出了精确的定义,它可以表述为:如果任意多条历史的权重之和都等于这些历史粗粒化后的权重,那么这些历史是自洽的。例如,一个粒子从t0时刻在x0位置出发,ti时刻处在xi或xi′位置,一直到tn时刻处在xn位置是一段粗粒化的历史,它的权重需要满足以下条件才是自洽的:




 ,曲线与对角线的交点代表部件可靠性阈值[25]
,曲线与对角线的交点代表部件可靠性阈值[25]


