溶出曲线是口服固体制剂最重要的基本属性之一，此外，复制注射剂和一些口服溶液剂也会要求与参比制剂进行体外溶出曲线对比。常用的溶出曲线比较方法包括f1差异因子法、f2相似因子法、多变量置信区间法和f2bootstrap法。

 在2015年2月5日发布的《普通口服固体制剂溶出度试验技术指导原则》中提到了f1法和f2法，因为f1法在溶出曲线比较时更宽松，所以在后续的指导原则中没有再出现，我们最常用的方法是f2法。f1和f2方法的原理及详细使用对比参见作者以前的文章《溶出曲线对比f1、f2法详解》。

当溶出曲线第一个取样时间点的溶出量相对标准偏差超过20%，或其他取样时间点的溶出量相对标准偏差超过 10%时，f2法不再适用。根据2022年11月8日发布的《已上市化学药品药学变更研究技术指导原则（试行）》溶出曲线研究的问答，此时可以选择多变量置信区间法或f2bootstrap法。此两种方法有各自的适用范围，作者在《溶出曲线对比法之f2bootstrap法》对f2 bootstrap法进行了详细的讲解。本文主要针对多变量置信区间法进行梳理，以期望同仁们在遇到类似问题时，能够合理选择评价方法。

一、何为多变量置信区间法？

为了理解多变量置信区间法，我们先了解下单变量置信区间法，虽然这个概念我们很少听说，但是我们实际工作中也有类似的应用，比如BE等效的判定标准即90%的置信区间下应80.00%~125.00%，就采用了置信区间法。

举个例子，12个计量单位的参比制剂15min的溶出数据分别为76.3、79.2、82.5、78.6、81.3、77.9、79.2、83.8、80.9、75.6、81.5、80.5，平均溶出度为79.78，标准差为2.45。仿制药15min的溶出数据分别是85.4、83.6、82.9、81.8、84.8、79.3、80.8、78.3、85.2、81.3、79.3、83.4，平均溶出度为82.18，标准差为2.43。如果用点估计两者溶出度之间的差异，则点估计差异D=82.18-79.78=2.4，从统计学角度来看，如果需要估计的更准确，应该使用区间估计，毕竟测定溶出选择的样品或溶出数据都会引入误差。根据区间估计的公式“点估计±误差”，下限L90=2.4-t22,0.05×合并方差；上限U90=2.4+t22,0.05×合并方差。其中t22,0.05可以查表得1.7171，其中22代表自由度，参比制剂自由度11（12-1），仿制药自由度11（12-1），所以合并的自由度是22。下限0.05加上限0.05等于0.1，因为1-0.1=0.9即90%，所以代表90%的置信水平。合并方差=√[(2.452+2.432)/11]=1.039。所以参比制剂和仿制药15min溶出度如果用区间估计，差异的下限L90=2.4-1.7171×1.039=0.62，差异上限U90=2.4+1.7171×1.039=4.18。虽然在药学对比时，采用点估计应用较多，其实区间估计更严谨，只是很多时候点估计已经能够说明问题罢了。

以上案例即单变量置信区间法，所谓的单变量是指仅有15min一个时间点这个变量。理解了单变量置信区间法，就比较容易理解多变量置信区间法了，所谓多变量，即不止一个时间点的变量，溶出曲线对比肯定不是一个时间点的对比，而是多个时间点的比较。

二、多变量置信区间法的步骤

对于批内溶出量相对标准偏差大于15%的药品，可能更适于采用非模型依赖多变量置信区间方法进行溶出曲线比较。2015年2月5日发布的《普通口服固体制剂溶出度试验技术指导原则》给出了多变量置信区间法的比较步骤。

2.1测定参比样品溶出量的批间差异，然后以此为依据确定多变量统计矩（Multivariate statistical distance，MSD）的相似性限度。

根据2.4的判定原则可知这一步非常重要，因为最终判定结果是否等效与参比制剂批间最大的相似性限度直接相关。所以，能够获得多批次参比制剂的数据是前提条件，尤其是参比制剂批次间的MSD越大越有利。参比制剂批次间每个时间点平均溶出量差异越大，MSD越大。

不过仿制药开发时，出于成本和注册的要求，一般仅采购三批参比制剂，这很可能无法获得较大的MSD，也就导致了仿制药和参比制剂溶出曲线采用此方法很难相似，判定的准确性存疑。为什么说准确性存疑呢？因为采用此方法计算参比制剂不同批次之间，仍然会判定为不相似，我们能说参比制剂批次间BE不等效吗？如下图所示的三批参比制剂，最大的MSD是参比2和参比3的1.1381，参比1和参比2的MSD是0.6974，参比1和参比3 MSD是0.9468。根据多变量置信区间法的步骤选择最大的1.1381为限度值，假设仿制药的溶出数据和参比1完全一致，仿制药（参比1）和参比3的MSD上限是2.4417，大于1.1381的限度，判定为不相似。将参比3与自身相比，计算的MSD上限是1.4949，仍然大于1.1381的限度，判定为不相似。因为参比制剂之间都无法判定相似，所以我们有理由认为此方法特别苛刻且准确性存疑。

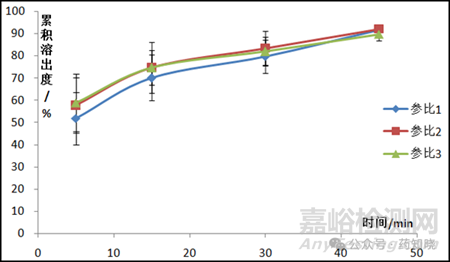
其实，根据作者对本法的思考和理解，这种方法更适合上市后的变更，因为有非常多批次的历史溶出数据，也就能找到最大的MSD，变更后的溶出曲线与变更前的多变量统计距对比，应该落到判定等效结果内，否则，判定为不等效。

2.2确定受试和参比样品平均溶出量的MSD。

参比制剂不同批次的MSD与受试和参比样品之间的MSD计算方法一致，但与参比制剂批次间的需求不同，受试和参比样品之间的MSD越小越好，这样才能得到更小MSD的90%置信区间上限。在做BE试验之前进行风险评估时或提交注册申报资料时，需要提交BE批次的受试制剂和参比制剂的MSD。根据下图MSD的计算公式可知，参比制剂和受试制剂的溶出曲线各时间点的距离差值越小，MSD越小。参比制剂和受试制剂各时间点溶出的RSD越大，MSD越小。

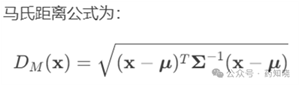
2.3确定受试和参比样品实测溶出量MSD的 90% 置信区间。

因为2.4项下的判定以置信区间的上限与参比制剂的相似限度进行比较，所以，需要使上限尽可能的小，才有可能判定相似。如何让上限尽可能的小呢？正如2.2项下表述，应该使参比制剂和受试制剂的溶出曲线各时间点的距离差值最小、参比制剂或受试制剂各时间点溶出的RSD最大。MSD本质上就是距离，各时间点的距离差值越小，两条溶出曲线越接近，MSD越小，这一点比较好理解。如何理解需要参比制剂或受试制剂各时间点的RSD大呢？可以参考下图， 假如参比和受试样品的溶出曲线RSD可以忽略（左图），那么两条溶出曲线的距离就是我们实际观察到的距离。假如参比和受试样品的溶出曲线RSD非常大（右图），平均溶出量不变，考虑到RSD波动后，受试样品和参比制剂可能互相包含，你中有我，我中有你，自然两者的MSD会变小。

2.4如果受试样品的置信区间上限小于或等于参比样品的相似性限度，可认为两个批次的样品具有相似性。

最后一个步骤是判定原则，至此，已经完成了样品的检验和数据统计，是否具有相似性一目了然。基于以终为始的目标，理解如何判定相似的基本原理，才能在一开始选择参比制剂的批次、受试制剂的溶出曲线开发目标做出最好的选择。

三、多变量置信区间如何计算？

多变量置信区间的计算会用到马氏距离，这个公式非常复杂，如果感谢兴趣可以继续看，如果看不懂也没有关系，能会用软件计算或者记住本文第二节的原理和结论即可。

根据FDA公布的参考文献（Statistical Assessment of Mean Differences Between Two Dissolution Data Sets），给出了一批参比制剂和一批仿制药的溶出数据，见表1。

表1  一批参比制剂和一批仿制药溶出数据

计算参比制剂和仿制药的协方差矩阵，对角线为各时间点的方差，15min的方差等于15min的单个溶出值减去15min的平均值，然后平方，6个平方求和后再取平均值。15min和90min的协方差等于15min的单个溶出值减去15min的平均值，再乘以90min的单个溶出值减去90min的平均值，6个乘积求和后再取平均值。完整的协方差矩阵见表2。

表2 参比制剂和仿制药协方差矩阵

将参比制剂的协方差矩阵和仿制药的协方差矩阵进行合并，即(S1+S2)/2，每一个对应数值相加除以2，得到新的复合协方差矩阵，见表3。

表3参比制剂和仿制药合并后的协方差矩阵

有了以上溶出数据和协方差矩阵，我们就能根据马氏距离的计算公式算出MSD。根据FDA参考文献中的案例，计算两个时间点15min和90min的MSD，更多时间点的计算类似，只是计算更为繁琐，篇幅限制，不再展示。

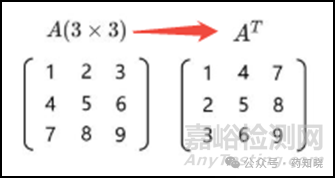
首先将马氏距离公式分成三个部分，（x-μ）T、∑-1和（x-μ），其中（x-μ）T是（x-μ）的行列变换，行变成列，列变成行，见下图。其实都是同一个数组，即15min和90min参比的平均溶出量减去仿制药的平均溶出量，记作（-17.54，3.39）。

据协方差矩阵表3，可知15min和90min的协方差矩阵由σ11=3.396，σ12=1.030，σ21=1.030，σ22=4.435构成。Σ矩阵和∑-1矩阵见下图。

其中det（∑）=σ11*σ22-σ12σ21=3.396*4.435-1.030*1.030=13.999；

       1/det（∑）=0.0714; 最后得出∑-1矩阵是

将已经求出的马氏距离公式的三个部分相乘，如下图，得到两个时间点的MSD=10.44，与FDA参考文献计算结果一致。

有了MSD值和上述计算结果，根据MSD的置信区间CR公式见下图。

其中K=(n2/2*n)(2*n-p-1)/[(2*n-2)*p]，n为每个溶出点的样本，本例为6片，P为比较的时间点个数，本例为15min和90min两个时间点，即P=2，可以计算K=1.35。F值可以查F分布表为3.01，可以计算出置信区间的上限=Dm+√（F/K）=10.44+1.493=11.93，下限=Dm-√（F/K）=10.44-1.493=8.95，与FDA参考文献值计算结果一致。因为F和K的值只和样本数量、取样点有关，所以，多变量统计距Dm一旦确定，置信区间上下限也就确定了。

四、结语

对于批内溶出量相对标准偏差大于15%的药品，多变量置信区间法在进行参比制剂和仿制药溶出曲线对比时，不是一个比较理想的方法，似乎是在碰运气，如2.1中所述，哪怕重合的曲线，因为参比MSD选择问题，都会导致判定不相似。f2bootstrap法似乎更理想，是首选方法。该方法更简单，也比较贴合实际情况，当每个时间点的平均溶出量较为接近时，容易判定为相似。

不管是f2相似因子法，还是多变量置信区间法或f2bootstrap法，都是体外评价溶出曲线相似的一个工具，对于仿制药来说，能够在体外评价相似又能够体内BE等效，当然是皆大欢喜的事情。如果通过各种努力真的无法做到全部介质中体外评价相似，但是体内BE等效了，那也不用怕，毕竟体内BE才是金标准。或者换句话说，我们选择的体外溶出方法是否过于苛刻了？