各阶段常见的典型失效机理

前段制程（FEoL）常见的失效机理

1）与时间相关的电介质击穿（TDDB）-- 栅极氧化物

2）热载流子注入（HCI）

3）负偏压温度不稳定性（NBTI）

4）表面反转（移动离子）

5）浮栅非易失性存储器数据保持

6）局部电荷捕获非易失性存储器数据保持

7）相变（PCM）非易失性存储器数据保持

后段制程（BEoL）常见的失效机理

1）与时间相关的电介质击穿（TDDB）-- 层间电介质/低k值/移动铜离子

2）铝电迁移（Al EM）

3）铜电迁移（Cu EM）

4）铝和铜腐蚀

5）铝应力迁移（Al SM）

6）铜应力迁移（Cu SM）

封装/界面常见的失效机理

1）因温度循环和热冲击导致的疲劳失效

2）因温度循环和热冲击导致的界面失效

3）因高温导致的金属间化合物和氧化失效

4）锡须

5）离子迁移动力学（PCB）--组件清洁度

本文对FEoL阶段的相变（PCM）非易失性存储器数据保持模型进行研究

在FD-SOI和FinFET CMOS技术中，传统浮栅非易失性存储器（NVM）集成在28nm和更小的制程上是一个重大的技术挑战。新的NVM技术基于特殊外来材料的功能特性，采用了与Flash存储器技术完全不同的物理机制，为28nm CMOS转变带来的工艺集成困难提供了更有效的解决方案。在这些常被称为“新兴存储器”的新型NVM技术中，最成熟的是相变存储器（PCM）。

相变记忆的基本机制是由斯坦福·罗伯特·奥夫斯基在20世纪60年代发明的，PCM通过诸如锗锑碲（GeSbTe）之类的薄膜硫族化物材料的电阻变化来存储数据，最常见的成分比例为Ge2Sb2Te5（GST）。

PCM的显著特点是薄膜层的电阻变化与材料在晶态和非晶态之间的热致相变有关，非晶态具有高电阻率，而晶态具有显著较低的电阻率。在PCM中，热刺激由施加在两个电极之间的电脉冲提供，这两个电极与位于它们之间的相变材料直接接触，电脉冲的形状和幅度决定了相变层是转变为非晶态还是晶态，存储器的状态是通过在低电场下测量其电阻来确定。PCM阵列截面图如下图所示。

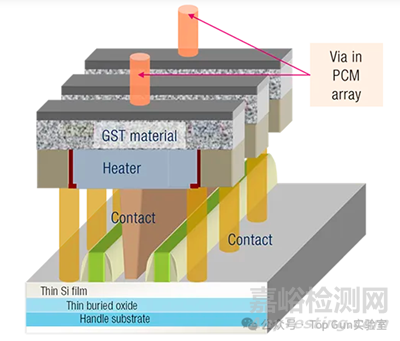
单比特每单元（single-bit-per-cell，SBC）有两个状态：SET和RESET。

1）SET状态：晶态（低电阻）的SET状态在热力学上是稳定的；

2）RESET状态：高电阻的非晶相有两个独立的电阻变化机制--结晶和电阻漂移。

漂移过程是由于硫族化物的结构重排和本征陷阱的动力学导致非晶相电阻率的稳定增加。由于漂移过程增加了高电阻非晶态的电阻，所以它不会导致SBC PCM器件的数据丢失。而结晶会导致电阻下降，因此结晶会导致PCM器件状态变化，造成器件数据丢失。

故PCM的数据保持能力可理解为避免非晶材料不期望的再结晶来保持高电阻RESET状态的能力。

相变（PCM）非易失性存储器数据保持模型：

如前文所述，相变存储器的晶态在热力学上是稳定的。非晶态会在温度条件下慢慢的通过固态非晶相中的晶核形成和晶体生长转变为晶态。为保证在存储设备的使用期限和使用条件下的数据保留，非晶态到晶态的结晶时间必须足够长。用于相变存储器的Ge2Sb2Te5相变合金的结晶遵循阿伦尼乌斯定律，在正常使用温度下非晶态到晶态的结晶时间为数年；因此，需要在高温下进行加速实验，以有效评估活性材料的结晶特性。

在PCM中，当一个最初被编程为高电阻RESET状态的单元在后续的读取操作中被发现处于低电阻SET状态时，那就发生了数据丢失（电阻下降到低于有效阈值失效电阻RFail时，RFail值取决于存储阵列中的传感算法）。电阻下降到低于RFail所需的时间被称为故障时间（TTF）。对于相对较低的温度（小于 200°C），晶核形成和生长机制都由原子扩散势垒和结晶动力学控制，可以用阿伦尼乌斯定律近似模型。其表达式为：

保留损失的热加速因子是通过将使用条件下的故障时间除以高温应力下的故障时间得到的：

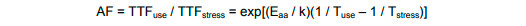
注：该模型适用于SBC PCM器件，该模型仅考虑了通过结晶（相变存储器材料的固有属性）导致的数据丢失，不适用与可能遇到的所有缺陷机制。

开发PCM的加速模型时，应考虑PCM的以下特性：

1）首先，在测试结构或专门设计的特性阵列中，通常在烘烤温度下监测 PCM 电阻，以实现更大的加速。在这种情况下，非晶态电阻率对温度的相关性和漂移现象的结合会改变RFail，导致计算出的Eaa出现误差。可靠的Eaa提取应通过在较长时间（较低烘烤温度）进行多次测量，并将阵列冷却至固定温度进行所有电阻测量来获得。

2）其次，PCM数据丢失一个被广泛接受的物理模型是通过所得混合相结构的类渗流传导。对同一器件进行重复保留测量的实验结果显示数据保持时间不同，从而证明了GST结晶的随机成分。因此，PCM数据保持时间预计具有随机性，因此需要对数据保持时间数据进行统计分析，研究表明该数据遵循威布尔统计。在提取Eaa时，需要进行充分的抽样，以满足威布尔统计数据的要求。

3）最后，关于PCM合金Ge2Sb2Te5的研究数据表明，擦/写循环对数据保持的影响相对较小（在某些情况下实际上改善了数据保持）。然而这种表现可能取决于特定的PCM合金或技术。因此，作为鉴定程序的一部分，应在循环之前和之后进行数据保留和加速模型分析。

注：JEDEC标准JESD91A，《Method for Developing Acceleration Models for Electronic Component Failure Mechanisms》，为测量提取Eaa提供了参考程序。

相变（PCM）非易失性存储器数据保持寿命预估示例：

目标：

计算加速因子（AF），即AF=TTFuse/TTFaccel；对由于非晶RESET状态下结晶而导致的PCM数据丢失的应力进行一次加速寿命计算。

假设条件：

1）正常使用条件为：55°C芯片温度

2）加速条件为：85°C

3）Ge2Sb2Te5表观活化能Eaa：2.5eV

AF计算公式：

AF=tretention,use/tretention,stress

AF=exp[(Eaa/k)(1/Tuse–1/Tretention,stress)]

假设条件代入计算：

AF=exp[(2.5eV/8.62x10–5eV/K)(1/(273+55)K–1/(273+85)K)]=1637

结论：对于 PCM 数据保持，在85°C下烘烤100h的选择相当于在55°C的使用条件下163,700h（18.7年）。

相关文献：

1）S. Lai and T. Lowrey, “OUM—A 180 nm nonvolatile memory cell element technology for stand alone and embedded applications,” IEDM Tech. Dig., 2001, pp. 803–806. 

2）F. Pellizzer et al., “A 90 nm phase change memory technology for standalone non-volatile memory applications,” Symp. on VLSI Tech., 2006, pp. 122–123.

3）S.H. Lee, Y.N. Hwang, S.Y. Lee, K.C. Ryoo, S.J. Ahn, H.C. Koo, C.W. Jeong, Y.T. Kim, G.H. Koh, G.T. Jeong, H.S. Jeong, and K. Kim,” Full Integration and Cell Characteristics for 64 Mb Nonvolatile PRAM”, Symp. on VLSI Tech., 2004, pp. 20-21. 

4）G.W. Burr, M.J. Breitwisch, M. Franceschini, D. Garetto, K. Gopalakrishnan, B. Jackson, B. Kurdi, C. Lam, L.A. Lastras, A. Padilla, B. Rajendran, S. Raoux, and R.S. Shenoy, “Phase Change Memory Technology,” J. Vac. Sci. Technol. B Volume 28, Issue 2, pp. 223-262 (March 2010). 

5）A. Pirovano, A. L. Lacaita, F. Pellizzer, S. A. Kostylev, A. Benvenuti, and R. Bez, “Low-field amorphous state resistance and threshold voltage drift in chalcogenide materials,” IEEE Trans. Electron Devices, vol. 51, no. 5, pp. 714–719, May 2004. 

6）A. Redaelli, D. Ielmini, U. Russo, and A. L. Lacaita, “Intrinsic data retention in nanoscaled phase-change memories—Part II: Statistical analysis and prediction of failure time,” IEEE Trans. Electron Devices, vol. 53, no. 12, pp. 3040–3046, Dec. 2006. 

7）Y.N. Hwang, C.Y. Um, J.H. Lee, C.G. Wei, H.R. Oh, G.T. Jeong, C.H. Kim, and C.H. Chung, “MLC PRAM with SLC Write-speed and Robust Read Scheme,” Symp. on VLSI Tech.,2010 pp. 201-202

8）A. Redaelli, A. Pirovano, I. Tortorelli, D. Ielmini, and A. L. Lacaita. “A Reliable Technique for Experimental Evaluation of Crystallization Activation Energy in PCMs”. IEEE Electr. Dev. Lett., 29(1): pp 41-43 (2008). 

9）U. Russo, D. Ielmini, A. Redaelli, and A. L. Lacaita, “Intrinsic data retention in nanoscaled phase-change memories—Part I: Monte Carlo model for crystallization and percolation,” IEEE Trans. Electron Devices, vol. 53, no. 12, pp. 3032–3039, Dec. 2006. 

10）B. Gleixner, A. Pirovano, J. Sarkar, F. Ottogalli, E. Tortorelli, M. Tosi, R. Bez, “Data retention characterization of phase-change memory arrays,” IRPS Tech. Dig., 2007, pp. 542–546. 

11）B. Gleixner, F. Pellizzer, R. Bez, "Reliability characterization of Phase Change Memory" NonVolatile Memory Technology Symposium (NVMTS), 2009 pp. 7 - 11

12）A. Redaelli, D. Ielmini, A. L. Lacaita, A. Pirovano, F. Pellizzer, and R. Bez, “Impact of crystallization statistics on data retention for phase change memories,” IEDM Tech. Dig., 2005, pp. 742-745.

13）J. W. Christian, The Theory of Transformation in Metals and Alloys. New York: Pergamon, 1965. 

14）U. Russo, D. Ielmini, and A. L. Lacaita, “A physics-based crystallization model for retention in phase-change memories,” Proc. IRPS Tech. Dig., 2007, pp. 547–553.