您当前的位置:检测资讯 > 科研开发
嘉峪检测网 2024-11-05 18:43
机械上有许多零件在工作时承受着随时间变化的应力,这种随时间做周期性变化的应力称为交变应力。例如,内燃机的连杆等受交变载荷而产生的应力、传动轴上各点因转动而产生的随时间做周期性变化的应力等。可以说绝大多数机械零件都是处于交变应力状态下工作的。习惯上将构件在交变应力作用下产生的破坏称为疲劳破坏。据估计,所有构件失效中,有 80%以上是属于疲劳破坏。
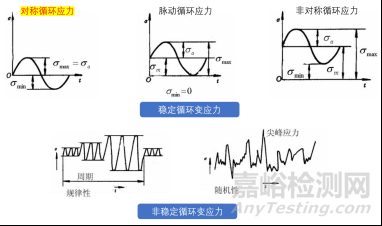
各类型交变应力
实践表明,构件在交变应力作用下的破坏形式与静载荷下全然不同。在交变应力下,虽然最大应力低于屈服极限,但在长期重复之后,也会突然断裂。即使是塑性较好的材料,断裂前也没有明显地塑性变形。这种现象习惯上称为疲劳破坏。
对疲劳破坏的一般解释是:由于构件的形状和材料不均匀等原因,构件某一区域的应力特别高。在长期交变应力作用下,在上述应力特别高的区域,逐步形成微观裂纹。裂纹的尖端处存在严重应力集中,促使裂纹逐渐扩展,由微观变为宏观。裂纹尖端一般处于三向拉伸应力状态下,不易出现塑性变形。当裂纹逐步扩展到一定限度时,便可能骤然迅速扩展,使物件截面严重削弱,最后沿严重削弱了的截面发生突然脆性断裂。

显微镜下的金属裂纹
疲劳曲线,即材料的S-N曲线,是材料所承受的应力幅水平与该应力幅下发生疲劳破坏时所经历的应力循环次数的关系曲线(如下图)。一般来说,材料所承受的循环载荷的应力幅越小,到发生疲劳破裂时所经历的应力循环次数越多。对于钢材等金属,当应力幅降至某一临界点时,S-N曲线就会变为水平,它表明该材料可以承受无限次应力循环也不会发生断裂,该点的应力就被称为疲劳极限(一般我们会以10^7作为疲劳极限的参考循环周期)。
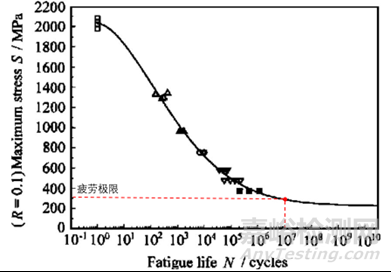
材料的S-N曲线
既然这样,是不是有了材料的S-N曲线,就可以通过应力直接判断其疲劳寿命?当然没有那么简单,前面我们说的S-N曲线是使用标准光滑试样,在对称循环应力下测试得到的结果曲线,但实际工况下,材料不仅尺寸、形状和表面情况是各式各样的,就连所受的应力肯定也是复杂多变的。影响疲劳寿命的因素有很多,最主要的就是平均应力的影响。S-N曲线是平均应力σm=0测试得到的结果,那如果σm≠0,又会对疲劳寿命带来什么影响呢?分两种情况:
平均应力σm<0,即应力比r<-1,材料整体受压缩平均应力,有利于疲劳裂纹的闭合;
平均应力σm>0,即应力比r>-1,材料整体受拉伸平均应力,疲劳裂纹更容易扩展,会降低材料的疲劳寿命;
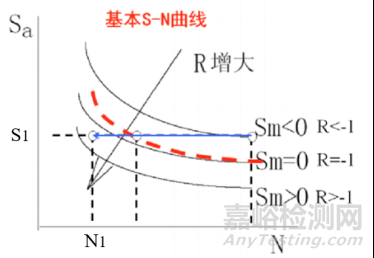
应力比对材料S-N曲线的影响
通过上图,可以发现在指定N1的循环寿命下,当应力比r提高时,或者说,当材料整体向受拉平均应力转变时,应力幅值就会下降;同样的道理,在指定应力幅S1时,随着应力比的提高,材料的疲劳寿命也会下降:
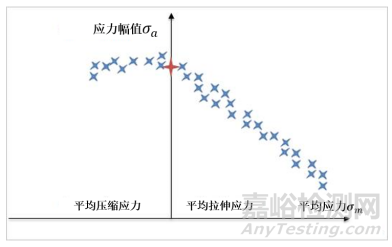
表示平均应力影响的疲劳极限曲线(Haigh曲线图)
因此可以发现不同的应力比,材料实际的S-N曲线也会不同,那为了利用S-N曲线预测材料的疲劳寿命,在实际工程中通常会进行平均应力修正,也就是按照疲劳寿命相等的原则,将平均应力不为零时的应力幅值等效为平均应力为0的应力幅值,然后借助对称循环应力条件下测得的S-N曲线来计算非对称循环应力时的疲劳寿命。
常见的方法是采取对平均应力进行校正。平均应力校正不需要多条SN曲线,也不需要在SN曲线之间进行插值,其方法是将应力循环转换为平均应力为零的等效应力循环。转换后的应力循环必须仍然包含相同的疲劳损伤潜力。这样,只需获得一条平均应力为零的SN曲线即可计算疲劳损伤。
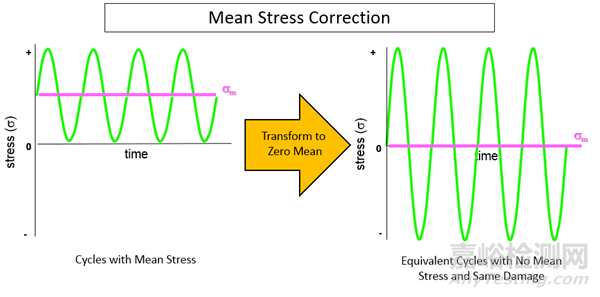
在上图中,是均值为正的应力循环被转换为均值为零的高幅值交变应力循环的示意图。如果我们只考虑应力幅,而忽略平均应力,显然上图右侧的循环会累积更多的损伤,下图是忽略平均应力时两个应力循环所造成的损伤累积比较。
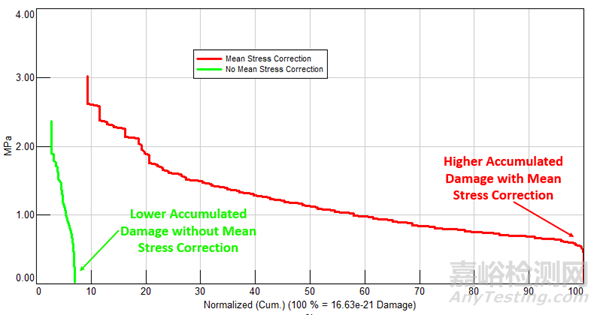
对于纯拉伸载荷谱,平均应力修正(红色)的累积损伤比没有平均应力修正(绿色)的大得多。当然,如果载荷谱中所有循环都是零平均应力,那么两者之间就没有差异了。那么如何将平均应力不为零的载荷谱进行修正以得到正确的等效疲劳损伤呢?这里我们需要用到Goodman-Haigh图。这个图相信做疲劳分析的你都比较熟悉了。
我们将应力循环的交变幅值和平均应力幅值绘制在Goodman-Haigh图上,如下图所示。纵坐标为应力幅,横坐标为平均应力。根据这两个值我们可以确定一个坐标点(标记为X)。下图左上角为一纯拉伸应力,因此该点落在了Goodman-Haigh图的右侧(第一象限)。
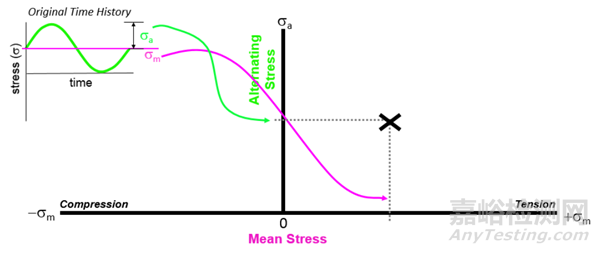
接下来,将材料的疲劳极限(endurance limit)和抗拉强度(ultimate strength)分布在纵坐标和横坐标上标记出来,并将两者连线。如下图中的蓝色实线。
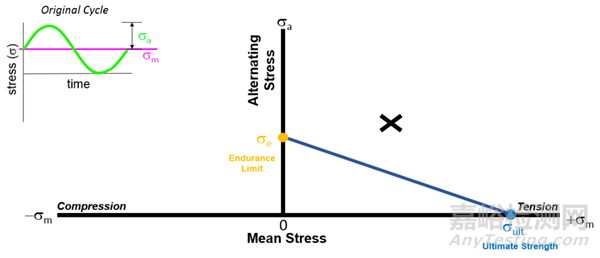
然后,通过前面我们的做的点(标记为X的)作一条和上面蓝色实线平行的一条线,如下图中的蓝色虚线所示。
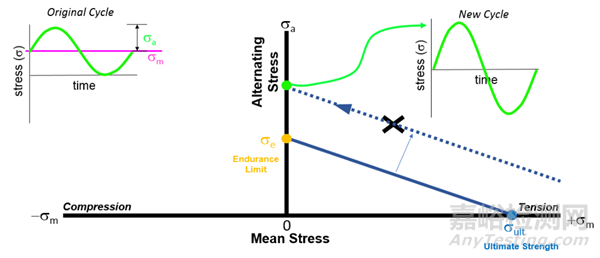
蓝色虚线与纵坐标轴的交点,即我们修正后的平均应力为零的交变应力的应力幅,可以看出,修正后的交变应力的振幅比原来的循环要大,这是对平均应力的一种补偿。
下面我们再来看看另外一种情况,纯压应力,如下图所示。同样的方法根据应力幅和平均应力做个点(标记为X),这时点出现在了Goodman-Haigh图的左侧(第二象限)。通过该点,同样做一条和蓝色实线平行的线,如下图中的蓝色虚线所示。蓝色虚线和纵坐标的交点即是修正后的平均应力为零时的应力幅。
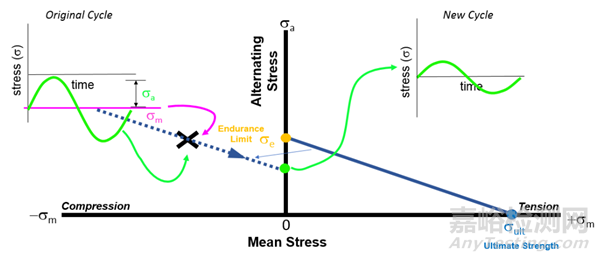
从上图中我们也能看出,当存在平均应力为压应力的载荷时,我们获得的修正厚度应力幅变小,从而损伤累积也会减少,疲劳寿命有所提高(压应力的作用)。
可能大家在做修正的时候,会遇到如下图所示的情况。通过X点作的线和纵坐标的交点落在了负值区域。
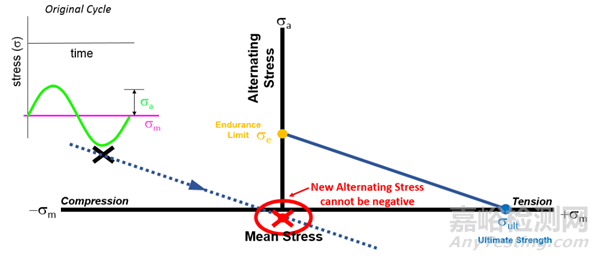
这时我们需要采取不同的投影、作平行线的方法。具体大家看下图就能明白。
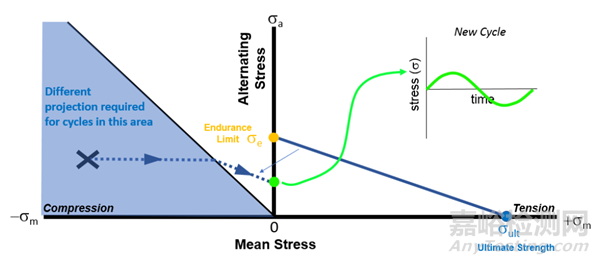

来源:Internet


