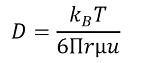前言
线速度是色谱学当中一个重要的方法参数,受流速、温度、色谱柱尺寸、流动相类型等因素的影响。在系统间转移或重现色谱方法时,线速度是需要重点考虑的因素之一。它也可以用来调整运行时间和/或改变色谱分离,所以理解线速度的影响在方法开发和故障排查过程中很重要。
一、VanDeemter方程
提到色谱学当中的线速度,就不得不说起VanDeemter方程。该方程是综合考虑了分离过程中引起峰展宽的物理因素、动力学因素和热力学因素后得到的单位柱长的总峰展宽与流动相流速的关系式。其具体表达式如下[1]:
由公式我们可以将VanDeemter方程(即柱效方程)理解成是由A、B/u、Cu三部分复合而成的曲线方程。以流速(cm/s)为x轴,以塔板高度HETP(mm)为y轴,分别对HETP=A,HETP=B/u,HETP=Cu,HETP=A+B/u+Cu作图,可得如下曲线图。
图1van Deemter H/u 曲线
接下来分别对公式中的A,B,C进行阐述说明。
二、涡流扩散效应
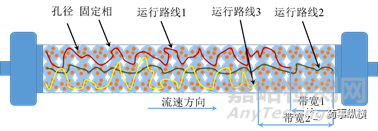
Van Deemter方程中的A项称之为涡流扩散项(Eddydiffusion),描述了由于色谱柱中固定相粒子的存在而引起的峰展宽。通俗的解释就是:色谱柱当中满充固定相填料,而这些填料的存在会阻碍溶质分子运行,填料粒径越大,溶质分子“绕行”距离就越远,或在填料孔径中停留的时间就越长。如图2所示,假设运行路线2为理想运行路线(长直路线几乎无绕行),运行路线1和运行路线3为非理想运行路线(绕行明显)。当溶质分子沿路线2和路线1流出时,此时谱带宽度较小(图2中标示为“带宽1”),离散程度较小,将得到如图3所示谱带展宽较小的红色流出谱图;当溶质分子沿路线2和路线3流出时,谱带宽度较大(图2中标示为“带宽2”),离散程度较大,将得到如图3所示谱带展宽较严重的绿色流出谱图。因此涡流扩散效应亦被称作“多路径效应”。该效应与填料的粒径、形状、孔径的形状及结构有关,而与流速的大小无关。填料粒径越大、填料形状越不规则、孔径的形状与结构越不规整,溶质分子的多路径效应越发明显,离散程度越大,柱效越低,峰展宽越严重。
图2涡流扩散示意图
图3涡流扩散对流出谱图展宽的影响示意图
三、纵向扩散效应
Fick定律:
J为扩散通量,用于量度微元时间内物质流过一个微元面积的量;
D为扩散系数;
∅为溶质浓度;
x为溶质分子迁移的位置长度
VanDeemter方程中的B项称之为纵向扩散项(LongitudinalDiffusion)。为解释纵向扩散效应,我们在此引入Fick定律[2]:由Fick定律可知,扩散通量与扩散系数以及浓度梯度(∂ø/ax)成正比。也就是说纵向扩散项与扩散系数以及浓差成正比。也就是说纵向扩散项与扩散系数以及浓差成正比。根据Einstein-Smoluchowski关系式可知扩散系数D的大小取决于绝对温度、分子的大小、流体的粘度以及分子的流速。从而可以得出如下结论:当流速增加或温度降低时,扩散系数越小,扩散通量越小,纵向扩散效应越不明显,反之,当流速减小或温度增加时,扩散系数越大,扩散通量越大,纵向扩散效应越明显。
Einstein-Smoluchowski关系式
KB为玻尔兹曼常数,为绝对温度
r为溶质分子的半径
µ为流动相的粘度
u为溶质分子的迁移速度
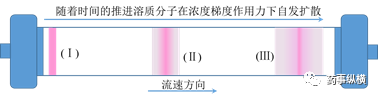
为了直观的说明纵向扩散效应,接下来将结合图3进行说明。假定玫粉色的深浅代表溶质分子浓度分布的差异,越深浓度越大,越浅浓度越小。溶质分子刚进入色谱柱入口时,溶质分子集中在(Ⅰ)区,未发生纵向扩散(深玫粉色区域)。由于(Ⅰ)区左右侧(空白区域)无溶质分子的存在,此时浓差效应明显,即梯度(∂ø/ax)作用力明显,溶质分子向空白区域扩散,呈现出(Ⅱ)区溶质分子的分布状态(中心深玫粉色区域变窄,左右两侧呈现对称的浅玫粉色区域)。随着时间的推进,溶质分子即将离开色谱柱时,呈现出(Ⅲ)区溶质分子的分布状态(中心深玫粉色区域进一步变窄,左右两侧呈现对称的浅玫粉色区域展宽)。对于一个指定的色谱柱,当流速增大时,溶质分子将以较短的时间通过色谱柱,此时用于纵向扩散的时间就相应减少,将会得到如图4所示谱带展宽较小的红色流出谱图;反之,流速小,溶质分子将会以较长的时间通过色谱柱,用于纵向扩散的时间相应增加,最终会得到图4中谱带展宽较严重的绿色流出谱图。
图3纵向扩散示意图
图4纵向扩散对流出谱图展宽的影响示意图
四、传质效应
Van Deemter方程中的C项称之为传质阻力项(MassTransfer)。与分离过程中样品组分在固定相和流动相之间的传质有关。
当流动相在色谱柱中流动时,如果不考虑固定相的作用,我们可以假定此时流动相在柱腔做层流运动。根据Poiseuille定律[4],此时流动相在色谱柱中的流速分布可以用
这也就是说流速和半径之间呈现二次抛物线关系,色谱柱轴心处存在最大流速。据此我们可以形象的画出色谱柱中的流速分布情况,如图5所示。通过上述的分析,也就是说在流动相中的溶质分子存在同流动相相同的速度场分布,而不同的流速分布就造成了溶质分子的传质过程的差异—色谱柱中心的溶质分子传质速率快,距离色谱柱中心越远传质速率越慢,从而造成了流动相中溶质分子的谱带展宽。而且展宽效应会随着流速的增大而增大。
图5不考虑固定相的影响色谱柱中流速分布示意图
图6流动相/固定相中溶质分布示意图
根据色谱学中的速度理论可知,流动相与固定相中的溶质分子的传质速率并不是无限大的,也就是说两相之间的分配平衡并不是在一瞬间就完成的,这个分配过程需要足够的时间去完成。如图6所示,假定(Ⅰ)区起始溶质分子在两相中的展宽一致(展宽1),经过一定的时间,流动相中的溶质分子以初始的速率继续运动,而固定相中的溶质分子由于“保留作用”将会以较慢速率运动或发生停滞从而造成谱带的继续展宽,如图6中的(Ⅱ)区所示(展宽2)。这个过程中,为了维持流动相与固定相中溶质分子的局部分配平衡,流动相中的溶质分子将会穿过相界面传质至固定相被吸附,而固定相中的溶质分子则会脱附并穿过相界面传质至流动相。随着流速的增加,流动相中的溶质传质速度增加,而用于两相平衡的相对时间减小,最终造成谱带的严重展宽。反之,流速减小,流动相中的溶质传质速率减慢,而用于两相分配平衡的相对时间增加,最终减弱谱带的展宽现象。
五、结束语
通过对vanDeemter方程的分析,可以得出色谱柱之间存一个最优线速度,此时可获得最低的塔板高度及最优的柱效。也就是说在此速度下可获得最优的纵向扩散—传质效应。填料粒径越小越均一,涡流扩散效应(多路径效应)越不明显。
六、参考文献
[1] van Deemter JJ, Zuiderweg FJand Klinkenberg A. Longitudinal diffusion and resistance to mass transfer ascauses of non ideality in chromatography. Chem. Eng. Sc. 1956, 5: 271–289. doi:10.1016/0009-2509(56)80003-1
[2] Adolph Fick, V. On liquiddiffusion. The London, Edinburgh, and Dublin Philosophical Magazine and Journalof Science. (1855), 10, 30.
[3] MA Islam, Einstein-Smoluchowskidissusion equation: a discussion. Physica Scripta 70 (2-3), 120, 2004.
[4] Salvatore P Sutera, RichardSkalak, The history of Poseuille’s law. Annual review of fluid mechanics 25(1), 1-20, 1993.