摘要：目的 探讨科研设计中， 计算样本含量时所需条件不足情形下的应对措施。方法 结合实例提出问题， 利用PASS11 软件解决问题。结果 通合理设置参数取值范围来计算样本含量时所需条件不足的问题；采用 Heish提出的方法应对 Logistic 回归协变量信息不足的问题；采用Lakatos 法应对生存分析样本含量计算时生存时间分布未知等问题。

结论 在科研设计中， 灵活地使用 PASS11 软件可以解决样本含量计算所需条件不足的一些问题， 但还有部分问题尚待深入研究。

医学科研设计阶段不可避免地要估计样本含量。高估样本量将会导致研究成本的增加， 同时会使暴露于危险性处理的受试者数量增加， 并且会导致研究周期的延长；样本量的低估会导致研究因为检验效能不足， 而没有发现总体间实际存在的差异 ［ 1 ］ 。故适量的样本含量， 既能满足医学科研的要求， 又能最大限度控制研究成本和研究风险， 保证研究效率。

科学研究中， 保证所估计的样本含量适当取决于很多因素。众所周知的基本影响因素有：检验水准 α 、 检验效能 1-β 、 个体间的变异 σ 、 允许误差 δ 以及单双侧检验 ［ 2 ］ ， 其他的影响因素与具体的设计类型有关。通常计算样本含量时， 都是已知以上的影响因素， 使用公式或者软件来计算样本含量， 但是在实际的科研设计阶段， 尤其是创新性的研究中， 有些参数即使通过查阅既往文献也未必能完全获得或者无法进行预试验来获得， 面对这些情况， 该如何计算样本含量呢？

本研究将结合科研工作者在研究设计阶段计算样本含量时面临的一些困惑， 结合实例提出问题， 并借助 PASS11 软件提出解决问题的方法。

1 计算样本含量所需条件不能精确取值问题的解决

实例 某医生欲比较肿瘤患者在接受新的治疗方案后与接受目前常规治疗方案后不同生存曲线的差异， 将花费 1 年时间来招募受试对象， 其后对患者的生存状况进行为期 4 年的随访。过去的临床研究经验表明对照组的 4 年生存率为 0.2 ， 实验组和对照组每年的失访率和非依从率大概分别为 5% 和 4% ，试估计在检验水准为 0.05 ， 检验效能为 0.8 的情况下， 需样本含量为多少？

该研究欲在设计阶段计算出区分不同生存曲线差异的样本量， 利用 PASS11 软件计算需要的参数有检验水准， 检验效能， 对照组的生存率， 风险比， 生存时间， 病例招募时间， 研究对象入组方式， 总的研究时间， 失访率和非依从率， 在上例中只有风险比这个参数是未知的， 通过查阅文献， 发现各文献中的风险比都是不同的， 在计算样本含量时取任何一篇文献中的风险比作为样本含量估计的参数都不合理。此时，可以利用文献资料得到一个风险比所在的范围， 如文献研究显示其风险比在 0.25 到 0.75 范围之间。于是本研究中， 选择 PASS11 中的Logrank Tests （ Lakatos ） 模块进行计算， 在模块对应的窗口输入已知的参数取值， 其中风险比 （ HR ） 项， 设置为：0.25 to0.75 by 0.05 ， 其含义为风险比从 0.25 到 0.75 之间每间隔 0.05取值 １ 次， 这样， 可得到不同风险比时所需样本含量， 见表 1 。

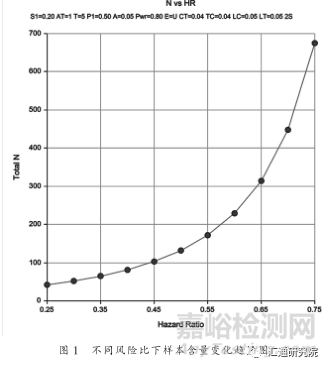
由表 1 和图 1 可以得出， 样本含量随风险比的增大而逐渐增大， 而且增长的速度也在逐渐增大。此时， 该如何确定样本含量呢？笔者有以下几点建议：（ 1 ） 若研究经费充足，且在设计的研究期限中能收集到足够的样本， 建议选取最大的样本含量， 对本例， 即 338 例；（ 2 ） 以研究期限内预期能收到的样本例数记作样本含量， 同时把表 1 附在研究设计中予以解释说明。

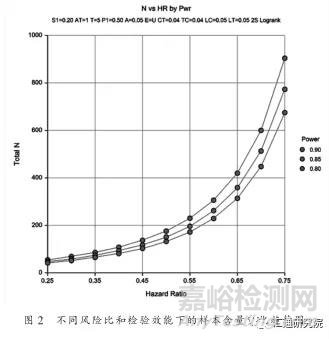
此外， 样本含量估计时， 当两个或多个参数存在不确定性时， 也可采用上述类似的办法给出随着参数变化时样本含量的变化范围。如上例中， 当期望的检验效能的取值为 0.8 到 0.9时， 可在 PASS11 中设置检验效能 0.8 to 0.9 by 0.05 ， 即检验效能取 0.8 ， 0.85 ， 0.9 ， 此时若风险比仍按 0.25 到 0.75 间每隔0.05 取值， 可得到 3×11 = 33 个样本含量， 见图 2 。

2 Logistic 回归样本含量计算时协变量信息缺失问题的解决

多因素分析时， 样本含量的估计常常是令科研工作者困扰的问题。通常大家采取的办法是， 取研究中拟纳入的协变量个数的 10～15 倍作为样本含量的估计值。但大家应该注意， 这个条件仅满足了多因素分析数学运算所需的最低要求， 但不能保证足够的检验效能；此外， 当研究设计阶段对协变量信息认识不全面时， 也给样本含量的估计带来了困难。

遇到以上的问题， 以 Logistic 回归为例， Heish ［ 3 ］ 提出使用方差膨胀因子来调整单个协变量计算出来的样本含量为多因素分析时所用，

如下式：

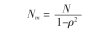
其中 N 是根据一个协变量计算出的样本量， ρ 为该协变量与余下 m-1 个协变量的复相关系数， N m 是校正后的 m 个协变量计算出的样本含量。

具体的实现可以通过样本含量计算软件 PASS11 ， 根据单个协变量的基本信息， 将计算所需要的参数输入到对应模块的窗口中， 通常所需要的参数主要有检验水准 α ， 检验效能 1-β ， 基线发病率 P0 ， 比值比 OR ， 目标协变量对其他协变量作回归时的决定系数 R 2 ， 由这些参数可以直接计算出校正后的样本含量 N m ， 这样既准确又便捷， 省去了使用公式计算的繁琐和复杂。下面结合实例来说明。

实例 一项探讨创伤后应激障碍和观看包含暴力内容后心率之间关系的研究， 已知心率是符合正态分布的， 心率对其他协变量作回归时的决定系数为 0.2 ， 该疾病在士兵中的发生率为 7% ， 求在检验水准为 0.05 ， 检验效能为 0.8 的情况下比值比达到 3 时的样本含量。

该研究已知一个协变量的信息， 在不知道其他协变量信息的情况下， 可以利用该协变量与余下协变量的复相关系数来计算样本含量， 选择 PASS11 中的 Logistic Regression 模块， 在对应 的 窗 口 中 输 入 已 知 的 参 数 取 值 ， 其 中 ：基 线 发 病 率 P0（ Baseline Probability that Y = 1 ） ：0.07 ， 比 值 比 Odds Ratio（ Odds1／Odds0 ）：3 ， 心率对其他协变量作回归时的决定系数R-Squared of x1 with Other X's ：0.2 ， 点击运行按钮， 计算出样本含量为 124 。

在上述的 Logistic 回归的样本含量计算中， 在已知一个协变量信息的情况下， 还需知道该协变量与其他协变量的复相关系数， 如何准确获得复相关系数， 也是今后值得深入研究的一个课题。

3 生存分析中生存时间分布未知时样本含量的估计

随访资料生存分析中样本含量估计时， 常假设生存时间服从指数分布 ［ 4 ］ ， Lachin-Foulkes 法是指数分布样本量测定方法的典型代表 ［ 5 ］ 。但医学实践中， 常见到生存时间不服从指数分布 ， 甚至无法确定生存时间分布的情 形， 此时若仍使用Lachin-Foulkes 法估计样本含量， 就会出现偏差。

1988 年， Lakatos 提出的方法 ［ 6 ］ 则可解决生存时间不符合指数分布， 且分布类型未知时样本含量的估计问题。该方法利用马尔科夫模型对每一个具体的随访过程拟合出一个独特的生存过程， 其中在各时段风险率， 删失率和病人的依从性都可以不同。陈素领等人曾介绍了该方法运用马尔科夫模型来进行样本含量计算的原理， 并用 VB 语言编写了计算程序， 给出了常见情况下的样本含量速查表， 方便读者查阅 ［ 4 ］ 。目前， PASS11软件中已经具备了 Lakatos 计算模块， 可以在模块中输入相应的参数取值， 就无需了解生存时间的具体分布类型， 同时也避免了烦琐的编程计算过程， 可以让医学工作者很方便地计算出样本量， 下面结合实例来说明在 PASS11 软件中对这类问题的实现。

实例 某研究者欲采用平行对照的临床试验来比较某新疗法与相对标准疗法治疗某疾病的生存过程。已知标准疗法 2 年生存率为 50% 。该研究预期用 1 年时间来招募患者， 其后进行为期 2 年的随访， 文献提示新疗法和标准疗法的年失访率和非依从率大概分别为 5% 和 4% 。研究者预计新疗法 2 年生存率可达 70% ， 请估计样本含量。

上例中， 试验组和对照组之间是相互独立的， 若新疗法的疗效消长幅度与标准疗法不同步， 且两疗法疗效消长幅度比例不恒定， 即不满足生存时间服从指数分布的假定 ［ 7 ］ ， 若此时不知道生存时间符合什么分布， 可采用 Lakatos 法估计样本含量。

在 PASS11 中， Log-rank 检验中包括 Lakatos 模块， 将上例中对应的参数取值输入到相应模块中去， 其中对照组的生存率 S1 （ Proportion surviving-control ）：0.5 ， 实验组的生存率 S2（ Proportion surviving-treatment ）：0.7 ， 生存 时 间 T0 （ SurvivalTime ）：2 ， 招募研究对象的时间 Accrual Time ：1 ， 研究对象的入组方式 Accrual Pattern ：Equal （ equal 表示研究对象是随时间均匀入组的）， 研究的总时间 Total Time ：3 ；由于随访研究中经常会出现失访和不依从的现象， 故 PASS11 模块中设置有实验组和对照组的失访率以及非依从率这 2 个参数项， 非依从性包括随访对象从实验组进入到对照组和随访对象从对照组进入的实验组这 2 种情况， 通过以上 2 项参数的设置会使得计算出的样本含量更符合随访实际情况， 从而达到更精确的目的。上例即通过文献查阅的方式获得新疗法和标准疗法 2 组的年失访率和非依从率， 输入以上参数后点击运行按钮， 就可以计算出其样本含量：在检验效能为 0.9 时， 实验组和对照组的样本含量分别为 130 ；在检验效能为 0.8 时， 实验组和对照组的样本含量分别为 98 。

4 讨论

当前， 针对样本含量计算的研究很多， 但大多数研究关注样本含量计算方法的改进探讨， 如吴艳乔等人提出使用 O／E法估计样本含量 ［ 8 ］ ， 李贤等人利用单因素裂区方差分析模型建立了两个和多个处理组重复测量设计所需样本含量的公式 ［ 9 ］ ，路浩等人提出用迭代非中心法来计算 Log rank 检验所需样本含量 ［ 10 ］ ；少数针对样本含量计算的实际应用的文献也多侧重于软件介绍， 如姚嵩坡等人使用 SAS 对假设检验中检验效能计算的实现 ［ 11 ］ ， 郭静等人提出利用 PASS2000 估计临床试验期中分析效能及样本大小 ［ 12 ］ 。

本文立足于从非卫生统计专业的科研工作者的角度， 针对医学科研工作者在研究设计阶段计算样本含量时常见的困惑，提出相应的解决办法。科研设计时， 特别是创新性研究时， 常遇到计算样本含量的条件不足的情况， 若不进行充分考虑， 而随意选取计算样本含量的参数， 会导致整个研究的失败， 浪费科研经费和科学家的研究生命。本文提出的方法， 解决了科研工作者的实际困难， 也使得样本含量的计算更符合医学实践。例如在实际临床试验研究中， 一般都是将随访时间划分为若干个区间， 然后在每个区间的开始或者结束时对受试者进行观察［ 4 ］ 。上文介绍的 Lakatos 方法也是将随访区间等分为 N 个区间， 这与临床随访研究的实际情况是相符合的。此外， 医学科研中大家可能还会遇到以下情况：由于受限于现实条件， 比如预算经费有限， 调查对象数量受限等等， 实际收集到的样本量与通过公式或软件计算出来的样本量有差距， 但是又不知道收集到样本含量使研究得出阳性结果的把握度有多大， 这时候可以计算在目前情况下所能获得的样本含量对应的检验效能能够达到多少， 如果检验效能仍然可以达到 0.8 以上， 说明对研究结果判断的可靠程度还是比较大的。

以上所讨论的样本含量的估计均是固定样本含量设计的情形， 即在研究设计之初确定样本含量， 并在全部研究对象完成研究之后进行统计分析。但是对于某些医学临床试验， 如果不论研究中发生什么情况，都需完成所有样本含量再进行评估，可能无法最大限度保护参加试验的患者的利益 ［ 13 ］ ；为此， 成组序贯设计 ［ 14 ］ 和适应性设计 ［ 15 ］ 样本含量的估计应运而生了， 如Hersey 等人报道的牛痘病毒裂解液治疗高危黑色素瘤的临床试验中， 由于期中分析时发现对照组的生存率明显高于预计， 于是研究者根据期中分析的信息对样本含量进行了调整 ［ 16 ］ ；To等人报道的一项评价宫颈内口缝合术预防早产的效果的研究中， 在期分析时由于疗效差异小于预期故对样本量进行了调整 ［ 17 ］ 。不过， 当前关于此类设计样本含量的估计仅限应用于设计类型比较简单的试验研究， 要推广到较复杂的科学研究中尚待时机。