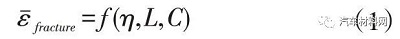摘要:针对超高强钢冷成形开裂的理论分析与预测问题,归纳了现有理论模型的特点、适用范围及其在超高强钢成形断裂失效分析的应用现状,指出由于超高强钢的脆性化倾向导致其断裂分析存在的难点。基于超高强钢的材料特性及其准脆性断裂的本质,对成形开裂理论预测模型与数值模拟方法提出建议。
关键词:高强钢 塑性成形 断裂失效 理论模型
1、 前言
金属成形过程的断裂失效一直是工程界关注的重点问题。作为目前汽车领域最经济可行的轻量化手段,高强钢的应用日益广泛且强度指标不断提升。但高强钢成形时具有与普通钢截然不同的断裂失效表现,如断前无明显颈缩、剪切断裂以及边缘开裂等,使得传统的断裂理论模型及适用于颈缩失效的成形极限图(FLD)手段均无法准确预测高强钢板的成形开裂。与此同时,高强钢种类的多样化以及成形加载路径的复杂化,对其断裂失效的分析提出了更为严苛的要求。目前,对超高强钢的成形断裂尚无准确可靠的理论预测模型,给汽车关键零部件及其成形工艺设计带来了严峻挑战。
本文首先归纳了韧性断裂模型的发展及其在高强钢成形方面的应用现状,指出了超高强钢断裂理论分析的难点。从超高强钢的材料特性及其脆性断裂本质的角度出发,对超高强钢成形开裂理论预测模型开发以及数值模拟方法提出建议。
2 基于韧性断裂损伤理论的耦合/非耦合模型
迄今为止,对高强钢成形的断裂分析和预测主要基于传统韧性断裂(损伤)理论。这些理论可分为3 类:基于细观孔洞形核、长大和聚合的多孔材料模型,连续介质损伤模型,唯象模型。前2 类考虑了损伤演化对塑性的影响,属于耦合模型,但由于在传统塑性本构模型中耦合了损伤变量,给模型求解和参数标定增加了难度,不易融入有限元代码。第3 类模型则独立考虑断裂(损伤)变量,忽略断裂(损伤)演化对材料断裂之前强度的影响,因此是非耦合模型。
2.1 多孔材料模型
多孔材料模型是基于孔洞理论,即基于物理推导的模型,主要包括以Gurson 模型为代表的细观损伤模型[1],以及McClintock[2]模型、Rice-Tracey[3]模型、GNT(Gurson-Tvergaard-Needleman)模型以及剪应力修正的Gurson 模型等。
1977 年,Gurson 在McClintock、Rice-Tracey 的孔洞生长模型基础上,为避开对细观和宏观耦合处理的困难,采用多孔材料的正则法则等连续介观思想,建立了含微孔材料连续介质单元体的体胞模型。由于Gurson 模型未考虑细观剪切带与孔洞扩展之间的交互作用,因此Tvergaard和Needleman[4]引入损伤函数来考虑材料失效时孔洞的迅速聚合,修正为GTN 模型。但GTN 模型认为孔洞的长大是导致最终断裂的微观机制,忽略了由剪切引发的微孔洞生长被抑制的因素。LI 等[5]将GTN 模型应用于旋压过程,表明GTN 模型适合预测材料隆起区的宏观裂纹,但不能预测负应力三轴度下变形区域的损伤演化。因此,近年来将剪切损伤引入GTN 模型。如XUE 等[6]考虑了损伤演变与第三偏应力不变量之间的相关性,使得改进后的GTN 模型集成了孔洞的剪切效应,适合描述低应力三轴度下的孔洞剪切机制。ZHOU 等[7]提出了修正的GTN 模型,将剪切损伤作为独立的损伤变量。然而,由于负应力三轴度作用下剪切扩展会加速损伤积累,改进的GTN 模型通常会给出更提前的断裂预测。对此,WU 等[8]将断裂应变重新定义为应力三轴度的函数,并对负应力三轴度下的孔洞形核函数进行修正,建立了更准确的适合于低应力三轴度η <-1/3 的损伤演化预测模型。
2.2 连续介质损伤力学模型
连续介质损伤力学(Continuum Damage Mechanics,CDM)通过建立一个损伤演变方程来表征一个连续损伤变量,借此描述局部微观缺陷的演变,并且损伤效应被直接引入到材料的本构模型中,以此描述材料的劣化过程[9]。CDM 考虑了损伤演化对材料塑性造成的影响,也属于耦合型模型。
CDM 的框架最早由法国学者LEMAITRE[10]建立,他采用刚度退化来描述材料在线性加载条件下的损伤,推导了一种基于连续损伤变量、等效应力和热力学体系的各向同性塑性损伤模型。然而,由于没有考虑剪切带局部化效应,基于CDM 的韧性断裂模型可能会导致复杂加载条件下损伤演化的预测偏差[11]。为此,CAO 等[12]提出了一种修正的基于应力三轴度的LEMAITRE 损伤模型,用于预测低应力三轴度和剪切主导载荷下的韧性断裂,同时提出一种获得由低到高的宽范围应力三轴度下损伤模型参数的方法。LIAN 等[13]以唯象的方式对传统的各向同性硬化LEMAITRE 损伤模型进行修正,考虑Lode 角对韧性断裂的影响以及在塑性变形过程中损伤引起的软化效应。YUE 等[14]采用包含Lode 角和微裂纹闭合效应的完全耦合延性损伤模型以及混合非线性各向同性和动态硬化的模型来探究DP600 钢在不同加载路径下的断裂行为。NGUYEN[15]通过引入Lode 参数来定义加载不对称条件,从唯象的角度考虑了剪切效应,提出了一种评估板料成形性能的连续损伤断裂模型。HUANG[16]通过考虑剪切效应的材料屈服面特性,建立了考虑Lode 参数影响的连续损伤模型(LCDM)。
2.3 非耦合的韧性断裂准则
非耦合准则单纯依据韧性断裂微观机理构建断裂发生时应力状态变量与应变状态变量之间应满足的数学关系,不考虑损伤与塑性变形相互耦合[17]。主要包括最大切应力准则、Cockcroft-Latham、Johnson-Cook、GISSMO 以及修正的Mohr-Coulomb(MMC)唯象型模型,以及基于经验的断裂成 形 极 限 图(FFLD)、Bao-Wierzbicki、Xue-Wierzbicki 断裂模型[18]。
早期的韧性断裂准则主要考虑宏观力学影响因子(如第一主应力、等效应力、静水应力或其中的多个组合)对断裂的影响。COCKCROFT 和LATHAM[19]认为,断裂主要与材料的最大主应力有关,当断裂位置的单位体积拉伸应变能达到临界破坏值时,材料发生断裂。OH 等[20]采用二维孔洞模型,对C-L 准则中的临界断裂应变能进行了修正解释,将该准则成功应用于轴对称挤压和拉拔工艺中。OYANE 等[21]描述了无孔材料和多孔材料韧性断裂的判据,给出了这些准则中材料常数的估算方法,并阐明了静水应力对断裂应变的影响机制。JOHNSON 和COOK[22]以无氧高导电性铜、工业纯铁、40CrNi2MoA 试样在不同应变率下的扭转试验、一定温度范围内的霍普金森杆试验以及各种缺口试样的准静态拉伸试验数据为对象,建立了考虑应变、应变速率和温度因素的累积损伤模型。但Johnson-Cook 模型以线性方式计算损伤积累,但实际中大多数零部件的损伤失效是以非线性方式积累。CLIFT 等[23]利用单位体积广义塑性功的临界值作为起裂条件,并用有限元模拟方法较为准确地预测了镦粗、轴对称挤压和拉伸3 种不同变形条件下材料的破裂。KO 等[24]对于传统韧性断裂准则预测中心翻孔破裂不准确的情况,综合考虑了Cockcroft准则中最大主应力对损伤的影响以及Oyane 准则中应力三轴度对断裂的影响,建立了一种新的韧性断裂准则。
研究表明,材料断裂行为受到多种因素的综合影响,如应变路径、损伤积累方式、应变率。GISSMO 断裂失效模型是一种基于应变路径的唯象模型,它综合考虑了材料在不同受力状态下不同的临界失效应变值、非线性应变路径及非线性损伤积累,反映了材料从受损开始、到损伤积累直至断裂的整个过程,因此可以较精确地描述材料变形过程以非线性损伤积累的失效。GISSMO 模型应用简便,已广泛应用于金属材料的断裂仿真评价中。
经典非耦合韧性断裂模型大都局限在高应力三轴度范围内,即η取值为1/3~2/3,不能在较大的应力三轴度范围内取得准确的预测结果。研究发现,在低应力三轴度下,材料(特别是高强钢)仍可能发生断裂。以BAO 和WIERZBICKI[25]为代表,为研究应力状态对AA2024-T351 韧性断裂的影响,设计了11 种具有不同几何形状的试样,进行了压缩试验、剪切试验和拉伸试验,获得了-0.3 <η <0.9 应 力 三 轴 度 范 围 内 材 料 的 断 裂 应变。不同试样断裂结果表明:断裂应变与应力三轴度η 的关系并不是单调递减的。在负应力三轴度(η <0)的压缩试验中发生的是拉长/扭转的剪切型韧性断裂;在高应力三轴度(η >1/3)的缺口拉伸试验中发生的是孔洞长大的拉伸型韧性断裂;在介于二者之间的低应力三轴度条件下( 0 <η <1/3),发生的是拉伸型和剪切型复合的韧性断裂[26]。BAO 和WIERZBICKI 的研究促进了韧性断裂研究领域的快速发展,后续许多学者开始将剪切作用机制引入韧性断裂准则,为考虑偏应力对断裂的影响,引入Lode 参数的概念,试图建立适用范围更广和准确性更高的新型韧性断裂准则。例如,XUE 等[27]应用近年来发展的塑性损伤理论,将应力三轴度和Lode 角相关性纳入材料的非线性损伤规律和材料劣化中,利用新模型成功预测出2024-T351 铝合金三点弯曲时的剪切开裂模式。GAO 等[28]描述了一种包含静水应力以及应力偏张量第二和第三不变量函数的各向同性韧性断裂模型,并对该模型进行了校准和验证。BAI 和WIERZBICKI[29]从屈服面与断裂轨迹的相似性角度出发,在等效断裂应变空间、应力三轴度空间和Lode 参数空间中建立了一个新的三维非对称韧性断裂模型。此后,BAI 等[30]基于描述脆性断裂的Mohr-Coulomb 准则,引入包含应力三轴度、Lode 参数与等效塑性应变的权函数,提出了修正MMC 模型,MMC 断裂准则可以很好地克服传统成形极限图在预测剪切断裂时的局限性,但当材料不符合σˉ=Aεˉn 应力应变关系时,预测效果不佳。为了提高模型预测的准确性,MOHR 和MARCADET[31]将Mohr-Coulomb 中的Tresca 等效应力转换为Hosford等效应力,建立了Hosford-Coulomb 准则(H-C 模型),通过试验证明H-C 模型克服了MMC 模型的局限性,可以较为准确地预测先进高强钢的韧性断裂起始位置。LIAN 等[32]在Bai-Wierzbicki 模型基础上,建立修正的应力三轴度和Lode 角影响的损伤起裂准则来描述微观尺度下材料的软化直至开裂过程。2012 年,LOU 与HUH[33]提出了一种新的韧性断裂准则来表征板料在塑性变形过程中孔洞的形核(等效塑性应变的函数)、长大(应力三轴度的函数)和剪切贯通(由归一化最大剪应力控制)的断裂行为,该模型将应力三轴度的临界值赋予恒定的-1/3,认为应力三轴度低于该值下,不会发生断裂。2014 年他们拓展了该准则[34],基于孔洞形核、生长和剪切贯通的微观机理,提出了一种宏观韧性断裂准则,为应力三轴度赋予一个可变的截断值来表征微观组织、Lode 参数、温度和应变率对金属韧性的影响,准确预测了从镦粗到平面应变拉伸不同应力三轴度下AA2024-T351 的断裂行为。穆磊[35]提出了一个基于孔洞形核和变形机制的非耦合型韧性断裂预测模型,使用无量纲化的最大主应力和无量纲化的最大剪应力来描述孔洞的长大机制和拉长扭转机制,将模型由主应力空间转化到由应力三轴度、Lode 参数和临界断裂应变构成的三维空间,获得了基于该模型的三维韧性断裂曲面模型。
研究表明,剪切断裂行为与材料组织均匀性有关,例如同种强度的双相钢,马氏体分布越均匀越不容易产生剪切断裂[36]。目前对剪切断裂的研究主要还是在应力应变关系以及韧性断裂准则等宏观的力学性能上。边缘开裂则归因于剪切工艺造成的边部微观缺陷对后续成形过程中材料的变形产生的影响,如切边质量较差的试样伸长率比切边质量好(实质是减小剪切断面微裂纹)的试样低10%[37]。通过不同的方式将材料的微观组织结构以及冲裁过程造成的边缘材料的残余应力、塑性应变、初始损伤、几何形貌引入到后续成形的仿真研究中[38-41],在简单加载路径的零件成形上实现了较好的预测效果。表1 为一些基于应变(力)的代表性断裂准则。
2.1 热水烫种消毒:先将蔬菜种子装入尼龙网袋中,再用30℃左右的温水浸种30分钟,促使种子上的病菌活化,这样容易杀死病菌。同时应不断搓洗,以洗掉种子上所带的抑制发芽的物质,而且也可使带茸毛(番茄)的种子湿透,以增加烫种效果。
3、 高强钢冷成形断裂特点及其理论预测难点
经典断裂力学认为,材料或构件中不可避免地存在裂纹、夹杂等各种缺陷。这些缺陷在外力作用下的扩展演化行为与材料特性密切相关,并由此建立针对脆性材料的线弹性和针对韧性材料的弹塑性两类理论[9]。随着高强钢强度级别不断提升,成形时其材料属性已进入事实上的“脆性”范畴(如延伸率<5%),且高强钢强化相马氏体体积分数越高,脆性断裂趋势越大[42]。事实上,从塑性变形的开始直至断裂,脆性材料与韧性材料在微观组织演化与宏观力学行为方面均存在着本质的差异。
a.断裂前塑性变形阶段的微观组织性能演化不同。客观上,实际材料均存在一定程度的不均匀属性。但韧性材料在外载荷作用下,可发生大范围、大程度的塑性流动变形,此阶段加工硬化的组织性能演化机制具有将材料内在不均匀性“分散”与“平均化”的趋势,从而使材料在失稳断裂前呈现一定“均质性”,因此材料可假设为“匀质”并用塑性应变确定其断裂阈值。
反之,脆性材料成形时只能发生小范围的塑性流动,原始微观非均匀缺陷(包括板侧的毛刺)的影响无法转移,因此对初始缺陷更加敏感。这也解释了材料特性与边缘开裂趋势的内在联系:韧性好的低强度级别材料可通过协调性变形弱化边部缺陷,边部开裂可能性较小;随着强度级别提高,材料对边缘微观缺陷敏感性增加,因此高强钢容易出现边缘开裂。
b.宏观的断裂表现不同。材料原始微观缺陷理论上是随机分布的。脆性材料由于变形量小而无法使缺陷效应“平均化”,性能参数试验值分散度很大,且测量误差相对于整体应变的占比较大。因此,由于脆性断裂的显著“突发性”与“随机性”,起裂与断裂的理论分析预测更为困难。
迄今为止,对高强钢断裂失效的分析大多基于韧性断裂的思路和假设,这难免造成结果的误差。例如,基于细观孔洞演化的模型可考虑应变路径等多因素影响,在高强钢断裂分析中已得到应用,但无法准确分析高强钢剪切断裂、边缘开裂的特殊失效形式;唯象试验判据简单易用,但难以考虑变形历史与加工硬化影响;半经验性CMD 宏观模型考虑了与应力/应变相关因素,但难以引入复杂加载路径的影响。材料的断裂包括高强钢的剪切断裂被认为由应力状态控制。基于应力的韧性断裂准则认为材料的应力状态达到某一临界断裂条件则发生断裂,如最大主应力准则、最大切应力准则、M-C 准则、MMC 模型等。理论上,这类准则预测脆性断裂更具优势,但由于未考虑变形过程中的应变历史,同样存在一定的局限性。此外,断裂是一种带有大应力梯度的局部现象,很难直接通过试验获取相关区域内与应力相关的状态变量。因此,这类准则在实际应用时,通常根据增量理论将基于应力的判据转换为基于应变的表达形式,如公式(1)。
表1 基于应变(力)的几个断裂准则
注:η 为应力三轴度;L 为Lode参数;θˉ为罗德角参数;A、C1、C2、C3、C4、C5、C6 为对应断裂模型的标定参数。
此时,模型回归到应变空间中,由高强钢脆性造成的应变实测分散性将引起标定参数较大的波动性,最终亦无法准确预测高强钢的断裂行为。总体上,由于实际高强钢成形断裂问题的复杂性,现有基于“韧性”断裂思路以及应变(力)的失效模型的预测精度有限。
研究发现,高强钢成形过程中会产生更多的局部塑性变形,通过简单拉伸试验得到的低延伸率(如<5%)或者应变来评价高强钢的成形性能具有局限性(过于保守),由此建立的恒等效应变断裂模型不再适用。相比之下,考虑不同应变路径的成形极限图(FLD)更为合理。但基于缩颈失稳理论建立的FLD 往往高估成形极限,也无法预测边缘开裂与剪切开裂等特殊开裂模式。
4、 超高强钢成形开裂预测理论研究思路
4.1 理论分析与预测模型
针对脆性材料的特殊断裂机制,已有一些异于传统思路的理论尝试。邢修三[44]将断裂理论建立于微裂纹发展动力学的统计基础上,导出有关宏观力学量;谢鹏等[45]基于边界效应模型(BEM),并引入细观结构参量—平均粒径G,建立脆性材料细观结构与宏观力学性能之间的关系;范书群等[46]根据缺陷累计失效概率的概念得到脆性材料破坏的概率公式;SINGH[47]利用离散与连续介质的方法研究了脆性断裂的一些基础问题。但将脆性断裂的思想用于高强钢失效分析的研究还未见报道,相关工作仍有待开展。
基于能量原理的力学准则通常具有明显的物理背景,而且能够同时考虑应变(及历史)、应力因素的综合影响。图1所示为基于“韧—脆性”断裂特性的高强钢失效行为多尺度精细模型构建思路。以高强钢“韧—脆性”材料特性为核心思想,结合微观机制引入复杂应力状态下的非均匀变形行为,并考虑宏观随机断裂特性与材料初始状态多重因素的影响,基于能量原理(ΔE=dε×dσ)构建针对“韧—脆性”材料的断裂失效模型。其中,从高强钢“韧—脆性”的材料本质特性出发,结合经典断裂力学理论,设计面向于高强钢的“韧—脆性”指标测试方法及试验系统,分析不同复杂应力状态及表面初始状态(表面预损伤)对高强钢断裂特征的影响规律,获取“韧—脆性”特征量化表达。微观方面,针对高强钢微观组织结构,基于非平衡统计的概念和方法引入微观缺陷分布函数(初始微裂纹密度分布函数),考察裂纹演化的微观机理,同时引入应变局部化因子以考虑高强钢在变形过程中的应变局部化效应;联立微观缺陷分布函数和应变局部化因子以表征材料“非均匀性”参量,进而更为全面的揭示高强钢材料微观组织结构对内部裂纹萌生及扩展的影响机制。基于应力/应变历史和微观断面特征推导成形极限应变能,获取成形极限应变能与“韧—脆性”指标、材料“非均匀性”参量之间的函数表达,从能量角度构建基于“韧—脆性”断裂特性的高强钢失效行为多尺度精细模型。
图1 基于“韧—脆性”断裂特性的高强钢失效行为多尺度精细模型
4.2 数值仿真
目前针对材料断裂失效的仿真大多采用FEM(有限元法)加单元删除法。该方法简单高效,但单元删除在一定程度上会导致系统质量和能量的损失,引起断裂特征的模糊化。此外,FEM 模拟结果的准确性也较大程度的依赖于精细化的网格尺寸,在裂纹形貌方面不具优势。
无网格方法是近年来兴起的一类新的数值方法,其中无单元Galerkin 法比较成熟,并已被应用于弹塑性问题分析[48]。无网格法采用直接点积分与稳定性增强项以及键断裂模型,保证了质量、动量与能量的守恒以及数值稳定性、收敛性,因而能够有效地模拟材料的失效与破坏,在模拟裂纹扩展的非连续体问题时具有显著优势。Livermore 公司在光滑粒子伽辽金法(Smooth Particle Galerkin Method,SPG)的框架下开发了键断裂模型。SPG是采用直接点积分(DNI)的Galerkin 法,它依照位移光滑理论导出了数值稳定性的增强项,从而抑制了弱形式常规DNI 导致的低能(沙漏)模式,能够获得稳定收敛的数值解,进而可用于材料的失效与破坏分析。如图2 所示,一旦材料达到失效条件,则键断开,相应位置积分点的应力置零,而非FEM 在应力置零的同时删除单元,从而避免了能量与模型特征损失。图3 为本文利用SPG 方法模拟某高强钢板折弯开裂的效果,结果显示键断裂处理方式在一定程度上保留了断裂特征。
图2 键断裂模型[48]
图3 利用SPG方法模拟某高强钢板折弯开裂
SILLING 等[49]提出的动力学法(Peridynamics,PD)也是一种无网格非局部数值方法。PD 基本方程采用积分形式代替传统连续介质力学的偏微分方程,避免了空间求导,在不连续处仍旧成立,无需进行连续性假设,解决了奇异性和计算效率问题,特别适合处理脆性材料的复杂破坏问题。如图4 所示,任波[50]利用PD 方法准确预测了汽车挡风玻璃受冲击作用下的破裂扩展行为。
图4 利用近场动力学法模拟玻璃受击破裂[50]
鉴于无网格方法在模拟材料自发裂纹成核和扩展问题中的巨大潜力,有理由认为,它将在高强钢断裂仿真分析方面取得应用。
5、 结束语
随着高强钢强度级别的不断提升,材料呈现明显的脆性化趋势并带来塑性变形能力大幅下降,其断裂具有与韧性材料截然不同的表现,如开裂的随机性、非均匀性以及初始缺陷的敏感性等。传统基于韧性材料的断裂准则无法准确分析和预测高强钢成形的开裂。鉴于超高强钢的材料特性,预测其断裂失效与成形极限需充分考虑(准)脆性的本质以及与此相关的复杂加载路径下的微观非均匀变形与宏观随机断裂特性,并计入应变、应力与材料初始状态多重因素的影响,才可能从根本上解决问题。
参考文献:
[1] GURSON A L. Continuum theory of ductile rupture by void nucleation and growth: Part I yield criteria and flow rules for porous ductile media[J]. Journal of Engineering Materials and Technology,1977,99(1):2-15.
[2] MCCLINTOCK F A, KAPLAN S M, BERG C A. Ductile fracture by hole growth in shear bands[J]. International Journal of Fracture Mechanics,1966,2(4):614-627.
[3] RICE J R, TRACEY D M. On the ductile enlargement of voids in triaxial stress fields[J]. Journal of the Mechanics and Physics of Solids,1969,17(3):201-217.
[4] TVERGAARD V, NEEDLEMAN A. Analysis of the cupcone fracture in a round tensile bar[J]. Acta Metallurgica,1984,32(1):157-169.
[5] LI H, FU M W, LU J, et al. Ductile fracture: Experiments and computations[J]. International Journal of Plasticity,2011,27(2):147-180.
[6] XUE L. Constitutive modeling of void shearing effect in ductile fracture of porous materials[J]. Engineering Fracture Mechanics,2008,75(11):3343-3366.
[7] ZHOU J, GAO X S, SOBOTKA J C, et al. On the extension of the Gurson-type porous plasticity models for prediction of ductile fracture under shear-dominated conditions[J]. International Journal of Solids and Structures,2014,51(18):3273-3291.
[8]WU H,XU W C,SHAN D,et al.An extended GTN model for low stress triaxiality and application in spinning forming[J]. Journal of Materials Processing Technology, 2018,(263):112-128.
[9]温彤.韧性损伤模型及其在金属塑性加工中的应用研究[D].重庆:重庆大学,1999.
[10] LEMAITRE J. A continuous damage mechanics model for ductile fracture[J]. Transactions of the Asme Journal of Engineering Materials and Technology, 1985, 107(107):83-89.
[11] KHAN A S, LIU H W. A new approach for ductile fracture prediction on Al 2024-T351 alloy[J]. International Journal of Plasticity,2012(35):1-12.
[12] CAO T S, GACHET J M, MONTMITONNET P, et al. A Lode-dependent enhanced Lemaitre model for ductile fracture prediction at low stress triaxiality[J]. Engineering Fracture Mechanics,2014(124-125):80-96.
[13] LIAN J H, FENG Y , S MÜNSTERMANN. A Modified Lemaitre Damage Model Phenomenologically Accounting for the Lode Angle Effect on Ductile Fracture[J].Procedia Materials Science,2014(3):1841-1847.
[14] YUE Z , CAO K , BADREDDINE H , et al. Failure prediction on steel sheet under different loading paths based on fully coupled ductile damage model[J]. International Journal of Mechanical Sciences,2019(153-154):1-9.
[15] NGUYEN N T, KIM D Y, KIM H Y. A continuous damage fracture model to predict formability of sheet metal[J]. Fatigue and Fracture of Engineering Materials and Structures,2013(36):202-216.
[16]HUANG X W,GE J Z,ZHAO J,et al.A continuous damage model of Q690D steel considering the influence of Lode parameter and its application[J]. Construction and Building Materials,2020(262):120067.
[17]杨婷,熊自柳,孙力,等.汽车用先进高强钢韧性断裂模型的研究与应用进展[J].锻压技术,2021,46(1):10-16+23.
[18]董梁.高强钢板材剪切边缘局部成形性能表征与开裂预测研究[D].上海:上海交通大学,2017.
[19] COCKCROFT M, LATHAM D. Ductility and the workability of metals[J].The Journal of the Institute of Metals,1968,96(1):33-39.
[20]OH S I,CHEN C C,KOBAYASHI S.Ductile Fracture in Axisymmetric Extrusion and Drawing—Part 2:Workability in Extrusion and Drawing[J]. Journal of Engineering for Industry,1979,101(1):36.
[21]OYANE M,SATO T,OKIMOTO K,et al.Criteria for ductile fracture and their applications[J].Journal of Mechanical Working Technology,1980,4(1):65-81.
[22] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates,temperatures and pressures[J]. Engineering Fracture Mechanics,1985,21(1):31-48.
[23] CLIFT S E, HARTLEY P, STURGESS C, et al. Fracture prediction in plastic deformation processes[J]. International Journal of Mechanical Sciences,1990,32(1):1-17.
[24]Y K KO,J S LEE,H HUH,et al.Prediction of fracture in hub-hole expanding process using a new ductile fracture criterion[J]. Journal of Materials Processing Technology,2007(187-188):358-362.
[25] BAO Y B, WIERZBICKI T. On fracture locus in the equivalent strain and stress triaxiality space[J]. International Journal of Mechanical Sciences, 2004, 46(1): 81-98.
[26]赵长财,杨卓云,董国疆,等.韧性断裂准则新发展及其在轻合金板材成形中的应用[J]. 中国有色金属学报,2020,30(8):11.
[27] XUE L, WIERZBICKI T. Ductile fracture initiation and propagation modeling using damage plasticity theory[J].Engineering Fracture Mechanics, 2008, 75(11): 3276-3293.
[28] GAO X S, ZHANG T T, ZHOU J, et al. On stress-state dependent plasticity modeling:Significance of the hydrostatic stress, the third invariant of stress deviator and the non-associated flow rule[J].International Journal of Plasticity,2011,27(2):217-231.
[29] BAI Y, WIERZBICKI T. A new model of metal plasticity and fracture with pressure and Lode dependence[J]. International Journal of Plasticity,2008,24(6):1071-1096.
[30]BAI Y,WIERZBICKI T.Application of extended Mohr-Coulomb criterion to ductile fracture[J]. International Journal of Fracture,2010,161(1):1-20.
[31]MOHR D,MARCADET S J.Micromechanically-motivated Phenomenological Hosford-Coulomb Model for Predicting Ductile Fracture Initiation at Low Stress Triaxialites[J]. International Journal of Solids and Structures,2015(67-68):40-55.
[32] LIAN J, WU J, Munstermann S. Evaluation of the cold formability of high-strength low-alloy steel plates with the modified Bai- Wierzbicki model[J]. International Journal of Damage Mechanics,2015,24(3):383-417.
[33]LOU Y S,HUH H,LIM S,et al.New ductile fracture criterion for prediction of fracture forming limit diagrams of sheet metals[J].International Journal of Solids and Structures,2012,49(25):3605-3615.
[34] LOU Y S, YOON J W, HUH H. Modeling of shear ductile fracture considering a changeable cut-off value for stress triaxiality[C]// International Journal of Plasticity,2014:56-80.
[35]穆磊.面向先进高强钢的韧性断裂预测模型研究与应用[D].北京:北京科技大学,2018.
[36]CHOI K S,LIU W N,SUN X,et al.Influence of Manufacturing Processes and Microstructures on the Performance and Manufacturability of Advanced High Strength Steels[J]. Journal of Engineering Materials & Technology,2009,131(4):41205-41213.
[37]祝洪川,孙宜强, 吴青松. 先进高强钢断裂性能研究[J].锻压技术,2015,40(12):115-119.
[38]WANG K,GREVE L,WIERZBICKI T.FE Simulation of Edge Fracture Considering Pre-damage from Blanking Process[J].International Journal of Solids and Structures,2015(71):206-218.
[39] CLIFF B, DAVID A, MICHAEL W . Predicting Failure during Sheared Edge Stretching Using a Damage-Based Model for the Shear-Affected Zone[J]. Sae International Journal of Materials & Manufacturing, 2013, 6(2): 304-312.
[40] SARTKULVANICH P, KROENAUER B, GOLLE R, et al. Finite element analysis of the effect of blanked edge quality upon stretch flanging of AHSS[J]. CIRP Annals-Manufacturing Technology,2010,59(1):279-282.
[41] UTHAISANGSUK V, PRAHL U, BLECK W. Stretchflangeability characterisation of multiphase steel using a microstructure based failure modelling[J]. Computational Materials Science,2009,45(3):617-623.
[42]罗娟娟,史文,黄群飞,等.高马氏体量双相钢的组织与性能研究[J].钢铁,2008,43(4):84-88.
[43] WIERZBICKI T, BAO Y, LEE Y W, et al. Calibration and evaluation of seven fracture models[J]. International Journal of Mechanical Sciences,2005,47(4-5):719-743.
[44] 邢修三. 金属穿晶脆性断裂统计理论[J]. 物理学报,1999(1):110-116.
[45]谢鹏,刘问,胡雨村,等.重组竹横向准脆性断裂的断裂参数[J].复合材料学报,2020,37(6):1466-1475.
[46]范书群,李永池,王志亮.脆性断裂的概率统计方法和应用[J].力学与实践,2007(2):57-60.
[47]SINGH G.Discrete and continuum studies of some fundamental issues in brittle fracture mechanics[D]. London:Imperial College London,2013.
[48] WU Y C, HU W, PAN X F, et al. Recent Developments of Smoothed Particle Galerkin (SPG) Method for Joint Modeling[C]// 16th International LS- DYNA® Users Conference,ANSYS SimuLive,2020.
[49] SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids,2000(48):175-209.
[50]REN B,WU C T,E ASKARI.A 3D Discontinuous Galerkin FEM with the Bond-based Peridynamics Model for Dynamic Brittle Failure Analysis[J]. International Journal of Impact Engineering,2017(99):14-25.
来源:期刊《汽车工艺与材料》作者:周银1 温彤1 方刚1,2 路胜海3 李冠楠4
(1.重庆大学材料科学与工程学院,重庆 400044;2.中国汽车工程研究院股份有限公司,重庆 401122;3.河钢集团钢研总院,石家庄 050023;4.河钢集团邯钢公司,邯郸 056015)