您当前的位置:检测资讯 > 科研开发
嘉峪检测网 2024-11-01 09:14
摘 要: 用氮气中水气体标准物质和内置水分发生器分别校准仪器,测量氮气中痕量水,并对测定结果的不确定度进行评定。不确定度来源主要包括单点线性校准、测量随机效应、影响准确测量的仪器参数和氮气中水气体标准物质4个方面,合成得到相对示值误差的扩展不确定度。当测试点的摩尔分数分别为4.3、51.8、99.7 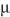 mol/mol时,采用标准气体校准时相对示值误差的扩展不确定度分别为5.5%、4.4%、5.2%,采用水分发生器校准时相对示值误差的扩展不确定度分别为6.1%、4.8%、6.3%。在测量区间1~100
mol/mol时,采用标准气体校准时相对示值误差的扩展不确定度分别为5.5%、4.4%、5.2%,采用水分发生器校准时相对示值误差的扩展不确定度分别为6.1%、4.8%、6.3%。在测量区间1~100 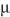 mol/mol范围内,离校准点越远,单点线性校准引入的不确定度越大,校准曲线的精确度和可信度越差;测试点量值越大,外部物理条件引入的不确定度就越大;不同校准途径对相对示值误差不确定度的影响不大。
mol/mol范围内,离校准点越远,单点线性校准引入的不确定度越大,校准曲线的精确度和可信度越差;测试点量值越大,外部物理条件引入的不确定度就越大;不同校准途径对相对示值误差不确定度的影响不大。
关键词: 石英晶体振荡法; 气体中痕量水; 不确定度
石英晶体振荡法水分仪应用石英晶体微天平技术原理[1],配置高灵敏度谐振式质量传感器,在测量高纯气体中痕量水方面的应用日渐广泛[2‒6]。式(1)~(3)可以诠释其测量原理[7‒9]:石英晶体在压电效应作用下产生频率稳定的机械振动[10],晶体谐振频率与质量负载之间的关系见式(1)[11],当晶体表面吸水涂层薄膜均匀分布、不因外力而变形,且晶体质量远大于吸附水分的质量时,谐振频率变化量与吸附水分的变化量成正比[8],由此式(1)转化为式(2),结合单点校准曲线,由式(3)计算出高纯气体中痕量水含量:
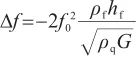 (1)
(1)
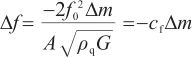 (2)
(2)
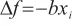 (3)
(3)
式中: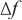 ——谐振频率变化值;
——谐振频率变化值;
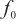 ——晶体固有频率;
——晶体固有频率;
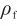 ——涂层薄膜密度;
——涂层薄膜密度;
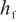 ——涂层薄膜厚度;
——涂层薄膜厚度;
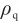 ——晶体密度;
——晶体密度;
G——AT切向剪切模量;
∆m ——水分吸附质量;
A——压电活性表面积;
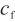 ——质量灵敏度系数;
——质量灵敏度系数;
b——校准曲线的斜率;
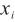 ——水分的摩尔分数。
——水分的摩尔分数。
目前国内使用的石英晶体振荡式水分仪主要由英国密析尔仪表公司和美国阿美特克有限公司两家企业生产,其内置水分发生器出厂时已进行定值和不确定度评定,可作为仪器的内部校准源,用于测量前的仪器标定。此外,也可用氮气中水气体标准物质作为外部校准源,在测量前对仪器进行标定。笔者分别用内、外校准源标定仪器,在测量区间1~100 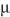 mol/mol范围内选取3个测量点,测量高纯氮气中痕量水含量,并进行不确定度评定及推论分析[12‒13],同时比较两种途径获得的示值误差及其扩展不确定度的差异,为仪器的校准溯源提供数据参考。
mol/mol范围内选取3个测量点,测量高纯氮气中痕量水含量,并进行不确定度评定及推论分析[12‒13],同时比较两种途径获得的示值误差及其扩展不确定度的差异,为仪器的校准溯源提供数据参考。
1、 实验部分
1.1 主要仪器与试剂
石英振荡法微量水分仪:QMA401型,摩尔分数测量精度为0.001 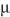 mol/mol,频率测量精度为0.000 1 Hz,内置水分发生器的生成水分摩尔分数标称值为54.2
mol/mol,频率测量精度为0.000 1 Hz,内置水分发生器的生成水分摩尔分数标称值为54.2 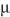 mol/mol,
mol/mol,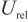 =2.3% (
=2.3% (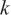 =2),英国密析尔仪表公司。
=2),英国密析尔仪表公司。
氮气中水气体标准物质:水的摩尔分数标称值分别为4.3、51.8、99.7 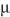 mol/mol,
mol/mol,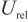 =2.0% (
=2.0% (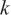 =2),上海基量标准气体有限公司。
=2),上海基量标准气体有限公司。
1.2 影响水含量准确测量的主要仪器参数
设置仪器参数的起始值:腔室压力为0.05 MPa,烘箱温度为40 ℃,气体流量为60 mL/min。保持其中两项参数不变,按表1中的调控量值,设置第3项参数的量值。每设置一次参数,测量氮气中水气体标准物质一次,然后进行吹扫净化残留的被测气体并平衡系统,进行下一步操作。重复上述过程3次,观察水含量测定结果的变化趋势,并计算最大变化量。调控仪器参数后水含量测定结果变化趋势如图1~图3所示,水含量最大变化量计算结果见表1。由表1可知,水含量变化量的绝对值为测试点量值的7.0%~20.4%,说明水分仪腔室压力、烘箱温度、气体流量是影响准确测定水含量的主要参数,3者的量值漂移会对测定结果产生较大波动。
表1 不同腔室压力、气体流量和烘箱温度下水的摩尔分数最大变化量
Tab. 1 Maximum variation of water content under different chamber pressures, gas flow rates,and oven temperatures ( μmol/mol )

注:校准点水的摩尔分数(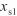 )为54.2 μmol/mol,测试点水的摩尔分数(
)为54.2 μmol/mol,测试点水的摩尔分数(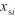 )为99.7 μmol/mol。
)为99.7 μmol/mol。
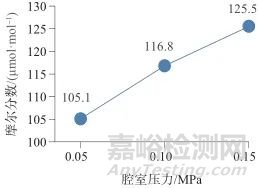
图1 不同腔室压力时水的摩尔分数测定结果
Fig. 1 Measurement results of water content (mole fraction) at different chamber pressures
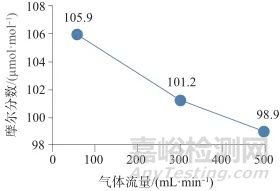
图2 不同气体流量时水的摩尔分数测定结果
Fig. 2 Measurement results of water content (mole fraction) at different gas flow rates

图3 不同烘箱温度时水含量(摩尔分数)测定结果
Fig. 3 Measurement results of water content (mole fraction) at different oven temperatures
1.3 水含量单次测量结果
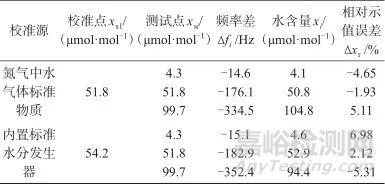
参照水分仪说明书设置最佳参数:腔室压力为0.1 MPa,烘箱温度为60 ℃,气体流量为300 mL/min。选择氮气作为载气,出口压力为实验室环境压力。仪器稳定后分别用氮气中水标准物质和内置水分发生器对水分仪进行校准,并对氮气中水气体标准物质进行测定,水含量的相对示值误差按式(4)计算,测定结果见表2。
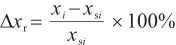 (4)
(4)
式中: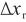 ——相对示值误差,%;
——相对示值误差,%;
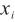 ——摩尔分数单次测定值,
——摩尔分数单次测定值,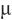 mol/mol;
mol/mol;
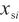 ——气体标准物质的摩尔分数,
——气体标准物质的摩尔分数,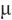 mol/mol。
mol/mol。
表2 氮气中水气体标准物质测定结果
Tab. 2 Measurement results of water gas standard substance in nitrogen
2、 测量模型
测量模型见式(4)。
灵敏系数:
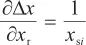 ;
; 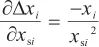
传播率:
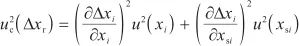
因此可得相对示值误差的标准不确定度:
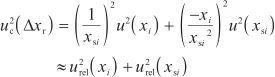 (5)
(5)
3、 不确定度来源
由测量模型可知,水含量相对示值误差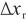 的不确定度主要来源于水含量单次测量值
的不确定度主要来源于水含量单次测量值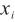 和氮气中水气体标准物质的摩尔分数
和氮气中水气体标准物质的摩尔分数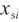 。其中单次测量值
。其中单次测量值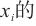 不确定度主要来源于单点线性校准、影响准确测量的仪器参数和测量的随机效应。
不确定度主要来源于单点线性校准、影响准确测量的仪器参数和测量的随机效应。
4、 不确定度评定
4.1 单次测量值引入的相对标准不确定度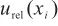
4.1.1 单点线性校准引入的标准不确定度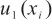
评定单点线性校准引入不确定度,由于不存在最小二乘法线性拟合,故不能参照CNAS—GL006:2019《化学分析中不确定度的评估指南》附录E,采用线性回归引入不确定度的评定方法。单点校正是实际意义上的两点校准,两点校准的校准点为(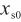 ,
,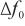 )和(
)和(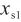 ,
, ),则单点可记为(0,
),则单点可记为(0,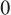 )和(
)和(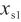 ,
,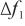 )。由于单点校准的零点是理论上的理想测量点,
)。由于单点校准的零点是理论上的理想测量点, 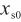 标准不确定度
标准不确定度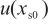 取0
取0 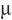 mol/mol,频率差值
mol/mol,频率差值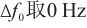 ,且
,且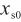 和
和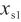 不相关,故用式(6)计算线性校准引入的标准不确定度
不相关,故用式(6)计算线性校准引入的标准不确定度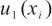 [14],测试点线性校准引入的标准不确定度见表3。
[14],测试点线性校准引入的标准不确定度见表3。
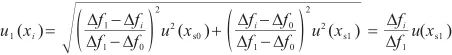 (6)
(6)
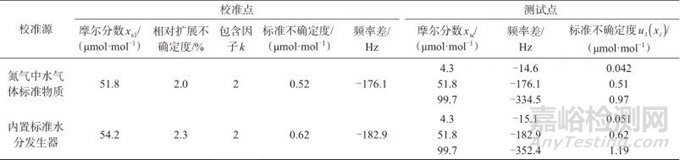
表3 测试点线性校准引入的标准不确定度
Tab. 3 Standard uncertainty introduced by linear calibration of test points
4.1.2 测量随机效应引入的标准不确定度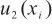
在测量过程中,即使是在重复性条件下的多次测量,也存在诸如取样、仪器调整、零位调整、对模拟式指示器的估读、环境条件的随机影响、操作过程中的随机性等效应而导致的测量结果分散。这种分散性称为随机效应,由测量随机效应引入的标准不确定度用重复性标准偏差计算。单次测量结果也包含随机效应引入的不确定度分量[15],按式(7)计算测量随机效应引入的标准不确定度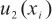 。
。
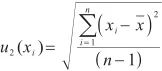 (7)
(7)
仪器测量气体后需要吹扫来净化残留并平衡系统,故每隔20 min测量氮气中水气体标准物质一次,连续测量6次。测量随机效应引入的标准不确定度见表4。
表4 测量随机效应摩尔分数测定值及标准不确定度
Tab. 4 Measurement value and standard uncertainty of mole fraction by measuring random effects ( μmol/mol )

4.1.3 主要仪器参数引入的标准不确定度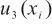
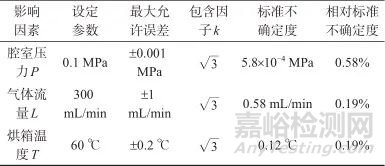
由于水分仪腔室压力、烘箱温度和气体流量的量值漂移对水含量测定结果影响较大,故评定不确定度时,需考虑上述参数最大允许误差引入的不确定度分量。选取水分仪的最佳测试参数,由于3个参数彼此独立不相关,且水分含量测定结果与腔室压力值正相关,与烘箱温度值、气体流量值负相关,故按式(8)分别计算腔室压力、气体流量和烘箱温度引入的相对标准不确定度,结果见表5。
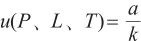 (8)
(8)
式中:a——被测量可能值区间的半宽度,等于仪器参数最大允许误差值的绝对值;
k——包含因子,按均匀分布,k=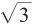 。
。
表5 腔室压力、气体流量和烘箱温度引入的相对标准不确定度
Tab. 5 Relative standard uncertainty introduced by chamber pressure,gas flow rate,and oven temperature
按式(9)和式(10)分别计算仪器参数引入的合成相对标准不确定度和标准不确定度,结果见表6。
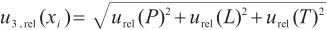 (9)
(9)
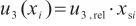 (10)
(10)
表6 仪器参数引入的不确定度
Tab. 6 Uncertainty introduced by instrument parameters

4.1.4 单次测量值的相对标准不确定度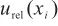
根据不确定度传播律,将单点线性校准、测量随机效应和影响仪器准确测量的主要参数引入的不确定度进行合成,得到水含量单次测量值的合成标准不确定度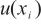 。由于上述各不确定度分量相互独立不相关,按式(11)和式(12)分别计算
。由于上述各不确定度分量相互独立不相关,按式(11)和式(12)分别计算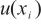 和
和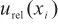 ,结果见表7。
,结果见表7。
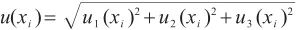 (11)
(11)
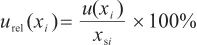 (12)
(12)
表7 水含量单次测量值的相对标准不确定度
Tab. 7 Relative standard uncertainty of single measurement value of water content

4.2 氮气中水气体标准物质的相对标准不确定度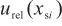
标准气体的相对扩展不确定度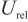 =2%,包含因子
=2%,包含因子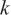 =2,则标准气体的相对标准不确定度:
=2,则标准气体的相对标准不确定度:
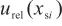 =1%
=1%
4.3 相对示值误差的合成标准不确定度和扩展不确定度
相对示值误差的标准不确定度和扩展不确定度分别按式(5)和式(13)计算,计算结果见表8。
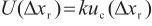 (13)
(13)
表8 相对示值误差的标准不确定度和扩展不确定度
Tab. 8 Standard uncertainty and extended uncertainty of relative indication error

5、 推论分析
单点线性校准引入的不确定度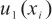 主要受测试点频率差值
主要受测试点频率差值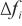 影响,离校准点越远,单点校准引入的不确定度
影响,离校准点越远,单点校准引入的不确定度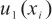 越大,呈线性比例关系,同时离校准点越远,校准曲线的精确度和可信度越差;影响准确测量的主要仪器参数引入的不确定度
越大,呈线性比例关系,同时离校准点越远,校准曲线的精确度和可信度越差;影响准确测量的主要仪器参数引入的不确定度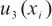 ,不受校准源的影响,主要取决于物理因素的最大允许误差和测试点的量值
,不受校准源的影响,主要取决于物理因素的最大允许误差和测试点的量值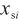 ,测试点量值越大,外部物理条件引入的不确定度就越大。测量中间点既为校准点又为测量点,另外两点分别靠近测量区间最小、最大值,佐证了在常用区间1~100
,测试点量值越大,外部物理条件引入的不确定度就越大。测量中间点既为校准点又为测量点,另外两点分别靠近测量区间最小、最大值,佐证了在常用区间1~100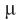 mol/mol内单点线性校准和仪器参数引入的不确定度的可靠性。
mol/mol内单点线性校准和仪器参数引入的不确定度的可靠性。
单点线性校准、测量随机效应和影响准确测量的主要仪器参数是水含量单次测量值标准不确定度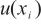 的主要来源,上述3种因素引入的不确定度分量
的主要来源,上述3种因素引入的不确定度分量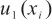 、
、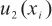 和
和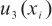 ,经合成得到水含量单次测量值的标准不确定度
,经合成得到水含量单次测量值的标准不确定度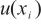 ,从而使
,从而使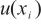 的评定更加合理。测量值的相对示值误差∆xr及其扩展不确定度
的评定更加合理。测量值的相对示值误差∆xr及其扩展不确定度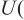
∆xr)均在仪器的允许±10%范围之内 ,两种校准途径的同一测试点U(∆xr)最大差值为1.1%,使用不同校准途径对测量值的示值误差不确定度影响不大。
6、 结语
石英晶体振荡式水分仪的校准属于单点校准,测量过程亦是单次测量,故需对影响水分含量准确测量的仪器参数、单点线性校准、测量随机效应和标准气体4个方面引入的不确定度分量进行评定,合成得到示值误差的测量结果不确定度。评定结果表明,使用不同校准途径对测量值的示值误差不确定度影响不大。实际工作中,虽然使用内置水分发生器校准仪器既便捷又经济实用,但其典型使用寿命为3年左右,且不恰当的使用和维护会造成量值的漂移和不确定度变大,合理有效地使用外部校准源氮气中水气体标准物质来校准仪器,不仅可以用来确定水分发生器的稳定性,还可获得与使用内部校准源相当的测量结果不确定度。
参考文献:
1 SAUERBRRY G. Verwendung von schwingquarzen zur wägung dünner schichten und zur mikrowägung[J]. Zeitschrift für Physik, 1959,155 (2):206.
2 张中慧,杨献奎,郑秋艳,等.电子气体中水分检测方法[J].化学分析计量,2023,32(2):103.
ZHANG Zhonghui,YANG Xiankui,ZHENG Qiuyan,et al. Detection methods of moisture in electronic gas[J]. Chemical Analysis and Meterage,2023,32(2):103.
3 曾晓晓,才来中,吴婷.石英晶体微天平在HL-2A 装置上的应用[J].核聚变与等离子体物理,2017,37(2):144.
ZENG Xiaoxiao,CAI Laizhong,WU Ting. Application of quartz crystal microbalance on HL-2A tokamak[J]. Nuclear Fusion and Plasma Physics,2017,37(2):144.
4 董了瑜,王成然,李志昂,等.氮中微量水分气体标准物质的制备[J].中国测试,2023,49(5):69.
DONG Liaoyu,WANG Chengran,LI Zhiang,et al. Preparation of trace water vapor in nitrogen gas reference material[J]. China Measurement & Test,2023,49(5):69.
5 邹春阳,王博伟,闫雪晴,等.石英晶体微天平(QCM)应用的研究进展[J].浙江农林大学学报,2020,37(5):1 006.
ZOU Chunyang,WANG Bowei,YAN Xueqing,et al. Application and development of quartz crystal microbalance (QCM)[J]. Journal of Zhejiang A & F University,2020,37(5):1 006.
6 杨会兵,王晓蕾,高澜,等.露点型温湿度传感器静态测试与性能分析[J].中国测试,2020,46(3):145.
YANG Huibing,WANG Xiaolei,GAO Lan,et al. Static test and performance analysis about temperature and humidity sensor by the dew point[J]. China Measurement & Test,2020,46(3):145.
7 李黎榕.石英晶体振荡法在气体中微量水分检测中的应用[J].化工设计通讯,2019,45(12):79.
LI Lirong. Application of quartz crystal oscillation method in the determination of trace moisture in gas[J]. Chemical Engineering Design Communications,2019,45(12):79.
8 周丽琴,刘桂礼,李东,等.石英晶体负载谐振频率的计算法测量研究[J].中国测试,2009,35(3):31.
ZHOU Liqin,LIU Guili,LI Dong,et al. Calculated method measurement study on load resonance frequency of quartz crystal[J]. China Measurement & Test,2009,35(3):31.
9 何高法,周传德,任建兵,等.药品包衣厚度测量系统晶振频率分析及实验研究[J].中国测试,2016,42(5):28.
HE Gaofa,ZHOU Chuande,REN Jianbing,et al. Analysis and experimental study of quartz crystal oscillation frequency of drug coating thickness measuring system[J]. China Measurement & Test,2016,42(5):28.
10 FERREIRA G N M,DA-SILVA A C,TOME B. Acoustic wave biosensors:physical models and biological applications of quartz crystal microbalance[J]. Trends in Biotechnology,2009,27(12):689.
11 PETRUNIN M A, GLADKIKH N A, MALEEVA M A, et al. Application of the quartz crystal microbalance technique in corrosion studies. A review[J]. International Journal of Corrosion and Scale Inhibition, 2020, 9(1):92.
12 周鑫,周泽义.光腔衰荡光谱法测定气体中微痕量水不确定度评估[J].计量学报,2012,33(2):178.
ZHOU Xin,ZHOU Zeyi. Evaluation of uncertainty in the determination of trace amounts of water in gases using cavity decay spectroscopy[J]. Acta Metrologica Sinica,2012,33(2):178.
13 周雄,刘伟,张小芹,等.微波透射法水分测定仪校准方法的研究[J].价值工程,2023,42(12):102.
ZHOU Xiong,LIU Wei,ZHANG Xiaoqin,et al. Research on the calibration method of microwave transmission moisture analyzer[J]. Value Engineering,2023,42(12):102.
14 张国城,张庆暖.对分析仪器两点线性校准引入不确定度的探讨[J].分析仪器,2015(2):63.
ZHANG Guocheng,ZHANG Qingnuan. Uncertainty evaluation of analytical instrument caused by two-point linear calibration[J]. Analysis Instrument,2015(2):63.
15 李慎安. JJF 1059—1999 《测量不确定度评定与表示》讨论之二十单次测量结果中是否就没有A类不确定度[J].工业计量,2008,18(6):40.
LI Shen′an. JJF 1059—1999 "Evaluation and Representation of Measurement Uncertainty" discussion part 20:Is there no Class A uncertainty in a single measurement result[J]. Industrial Measurement,2008,18(6):40.
引用本文: 蔡光华 . 石英晶体振荡法测量气体中痕量水的不确定度评定[J]. 化学分析计量,2024,33(9):111. (CAI Guanghua. Uncertainty evaluation for the determination of trace water in gas by quartz crystal oscillating method[J]. Chemical Analysis and Meterage, 2024, 33(9): 111.)

来源:Internet


