摘  要 / Abstract

 

随着历史数据和同期外部数据等真实世界数据（RWD）资源及质量日益提升，越来越多的研究者开始关注使用外部数据为药物和医疗器械的安全性及有效性评价提供更全面有效的证据支持，特别是在难以实施大样本随机对照试验的罕见病和儿科疾病领域。因此，创新的分析方法对于高效利用这些数据变得尤为重要。在此背景下，本文旨在系统梳理并介绍临床试验中外部数据借用的研究方法，同时对比各种研究方法的优势与劣势，以期为研究者提供有价值的参考，进而推动临床试验在利用外部数据时更加高效、准确。

 

With the ongoing improvement in the resources and quality of real-world data (RWD), including historical data and concurrent external data, an increasing number of researchers are focusing on leveraging external data to provide more comprehensive and effective evidence for evaluating the safety and efficacy of drugs and medical devices. This is particularly crucial in fields such as rare diseases and pediatrics, where conducting large-scale randomized controlled trials is often impractical. Therefore, innovative analytical methods are essential for efficiently utilizing these data. In this context, this paper aims to systematically review and introduce the research methods for borrowing external data in clinical trials, while comparing the advantages and disadvantages of various methods. The goal is to provide valuable references for researchers and promote more efficient and accurate use of external data in clinical trials.

 

关 键 词 / Key words

 

真实世界研究；外部数据；药物和医疗器械；临床试验；统计分析方法

 

real-world study; external data; drugs and medical devices; clinical trials; statistical methods

 

1、背    景

 

随机对照试验（randomized controlled trial，RCT） 是评估药物有效性和安全性的金标准。对于支持注册上市的药物疗效评价，大多数情况下RCT 是必须的。然而，由于成本高昂、研究周期长、招募患者困难和伦理限制等因素，实施充分的RCT 可能会面临多种挑战，特别是儿科疾病和罕见病领域的研究[1]。试验外部真实环境中产生的数据（如医院信息系统数据和自然人群队列数据等）以及各种同期/ 历史外部试验积累的数据，即真实世界数据（real world data，RWD），可能承载大量关于药物有效性和安全性的信息。如果能够利用科学合理的设计策略和因果推断方法，通过借用这些信息使尽量少的受试者分配至疗效较差甚至无效的对照治疗，同时减少所需样本量，加速有效治疗药物惠及患者，将是非常合乎伦理性且必要的。

 

然而，由于试验设计、患者群体以及医疗水平等多种因素的综合作用，外部数据与当前试验数据之间往往存在异质性。若未经充分评估，直接在当前试验中利用这些外部数据，很可能导致疗效估计产生偏倚。目前，越来越多借用外部RWD 信息提高临床试验效率的统计方法被提出。本文将对此进行系统梳理介绍，并对比各种研究方法的优势与劣势，以期为研究者在临床试验中更加高效、准确地利用外部数据提供有价值的参考。

 

2、基本定义

 

2.1 外部数据可借用性的评价标准

 

在当前试验的设计和分析中使用历史对照数据面临5 个重要问题：什么是相关的历史数据？历史数据能提供多少额外的患者？如何评估历史数据和当前数据之间的一致性？新的研究需要多大的样本量？如何将历史数据纳入分析？

 

Pocock[2] 指出，可接受的历史对照数据必须满足6 个条件：①精确定义的标准治疗。历史对照组所接受的治疗必须是精确定义的，并且与随机化对照组接受的治疗相同。②近期临床研究的一部分。历史对照组必须来自一个近期的临床研究，该研究包含了与新试验相同的患者资格要求。③一致的评估方法。治疗评估的方法在历史对照组和新试验中必须是一致的。④可比较的患者特征分布。历史对照组中患者的重要特征分布应该与新试验中的特征分布相似。⑤同一组织实施的研究。以前的研究必须在同一组织实施，且主要由相同的临床研究者进行。⑥无其他预期结果差异的因素。没有其他因素可能导致人们预期在随机化对照和历史对照之间会有不同的结果。例如，如果新研究的患者招募速度更快，可能会让人怀疑前一研究中研究者参与的积极性，从而可能导致患者选择过程的不同。

 

以上这些条件的设定旨在最大程度降低历史对照组可能引入的偏倚，进而确保历史对照数据在与新疗法进行比较时具备更高的可信度和可靠性。尽管某些标准显得较为严苛，但它们为选择和评估相关的外部研究提供了重要的参考依据。

 

2.2 符号定义

 

基于混合设计背景，假设当前试验是一个双臂RCT，对照组部分拟借用外部对照数据。以Y 表示结局变量，X 表示观测到的协变量向量，Z 表示研究指示变量。其中Z=1 表示数据来自当前试验；Z=0 表示数据来自外部对照数据。T 表示治疗指示变量，T=1 表示受试者被分配到试验组，T=0 表示受试者被分配到对照组。Dt、Dc、De 分别表示当前试验组的数据、当前对照组的数据以及外部对照数据。Nt、Nc、Ne 分别表示当前试验组、当前对照组以及外部对照数据的样本量。θt、θc 和θe分别表示当前试验组、当前对照组和外部对照数据的感兴趣参数。

 

3、借用外部数据的统计学方法

 

现有在临床试验中借用外部数据的流行方法大体上可分为基于Bayes 理论的方法和基于传统频率学派理论的方法。

 

3.1 基于Bayes 理论的方法

 

 表1 汇总了几种基于Bayes理论的方法的优缺点以及主要思想。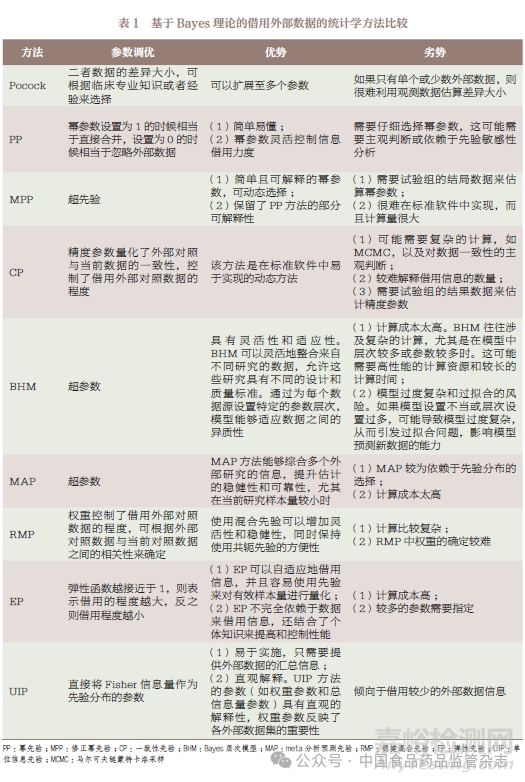

3.1.1 Pocock 方法

 

Pocock 方法[2] 引入服从正态分布N(0,σ2δ) 的随机变量δ=θc-θe，用 σ2δ衡量研究间可能的异质性程度。基于Bayes 理论可得到θc 的后验分布，见公式（1）。其中，π(θc) 为模型参数的无信息先验；L(θc|Dc) 是当前对照组数据的似然函数；L(θc-δ|De)是考虑随机变量δ 的外部对照数据的似然函数。若存在K 个满足要求的外部对照数据，分别用D1,D2,…, DK表示，即De=(D1,…,DK)，则后验分布见公式（2）。即允许不同外部对照数据的异质性偏倚δk 不同。由于难以通过外部对照来精确估算σ2δ，该方法建议为σδ预先设定一个值，并基于不同的σδ 值进行敏感性分析。

 

3.1.2 幂先验

 

幂先验（power prior，PP）方法由Chen 等[3] 于2000 年提出，该方法将外部对照数据信息利用似然函数的幂指数打折后作为当前对照数据的一个先验，即：

 

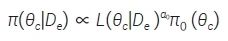
其中，π0 (θc) 是θc 的初始先验分布，通常选择无信息先验；L(θc|De) 是外部数据的似然函数；α0为幂参数，取值为0~1，表示对外部数据信息打折α0后借用；α0=1 相当于直接合并所有的外部对照数据到当前研究中，即完整借用外部信息，适用于当前数据和外部数据完全一致时；α0=0则θc的先验分布就是其初始先验分布，即π(θc|De)=π0 (θc)，表示完全不借用外部信息，适用于当前数据与外部数据完全不一致的情形。基于Bayes 定理， 利用当前对照组的数据更新先验分布π(θc|De)，从而得到对照组参数θc的后验分布，见公式（3）。其中L(θc|Dc) 是当前对照组的似然函数。

 

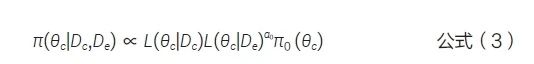
该方法可以直接扩展至借用多个外部数据的情形，假设第i 个外部数据的幂参数为αi, i=1,…,K，则多个外部对照数据的PP 为：

 

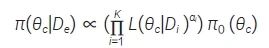
同理，基于Bayes 原理利用当前数据对π(θc|De) 更新，得到参数θc的后验分布。

 

对于取值固定的幂参数α0的取值选择，目前已有较多确定方法（表2）。此外，也有一些拓展的幂先验方法。

 

（1） 正则化幂先验（normalized power prior，NPP）方法[3]。将幂参数当作一个随机变量，构造θc和α0 的联合先验分布，见公式（4）。但上述先验违反了似然性原理[8]，导致α0取值趋于零。

 

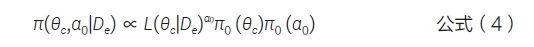
（2）修正幂先验（modified power prior，MPP）方法[9-10]。通过引入归一化常数对NPP 方法的联合先验分布进行校正，见公式（5）。

 

 

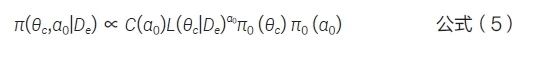
其中C(α0)=1/∫L(θc|De)α0π0(θc)dθc。MPP 分母中包含积分项，大多数情况下几乎不可能推导出该积分的解析表达式，采用马尔可夫链蒙特卡洛采样（Markov chain Monte Carlo，MCMC）时计算复杂度和耗时都较高，影响了实用性和效率。对此，Gravestock和Held[11] 提出了一种经验Bayes（Empirical Bayesian）方法来确定幂参数，其核心思想是寻找使得幂参数的边际似然函数达到最大的α0，即：

 

该方法极大地减轻了计算负担，并且可直接扩展至多个外部数据的情形，见公式（6）。其中α=(α1,…,αk)T。

 

 

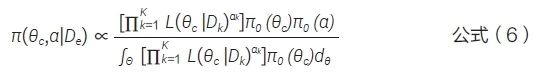
3.1.3 一致性先验

 

一致性先验（commensurate prior，CP）[12] 对PP 进行了自适应改进，通过衡量内外部数据之间的一致性程度调整PP。该方法假设当前对照数据与外部对照数据所具有的潜在参数不同，即θc ≠ θe。在该假设下，θc的CP 定义为一个条件先验分布，其均值为当前对照数据中的参数θc，精度为τ。在试验开始之前，θc 和θe 的联合后验分布为，见公式（7）。τ 是一个超参数，量化了内外部数据的一致性，控制了合并外部对照数据的程度。τ 值越大表示一致性越强，借用外部数据的程度越大。τ 也能作为一个随机变量而不是固定的值，其先验分布的选择与 meta分析中研究间方差参数的先验相似。此外，Murray 等[13] 还提出了一种灵活的半参数方法，并将该方法扩展到了分段指数生存分布（piecewise exponential survival distribution）。

 

 

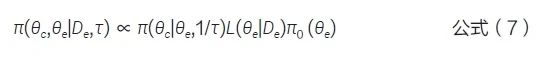
3.1.4 Bayes 层次模型

 

Bayes 层次模型（Bayesian hierarchical model，BHM）[14]通常假设不同研究中的感兴趣参数均源自同一个正态分布，利用其方差τ 反映研究间的异质性，从而控制外部数据的借用程度。τ值越大表示异质性越大，从而借用的信息越少。在此基础上也有各种扩展方法（表3）。

 

 

3.1.5 Meta 分析预测先验

 

假设存在K个满足要求的外部数据，分别用D1, D2,…, DK表示K个外部对照研究中的数据，记为De=(D1,…,DK)。令θ1,θ2,…,θK表示每个外部数据中感兴趣的参数。假设θ1,θ2,…,θK,θc是可交换的，模型表示为：

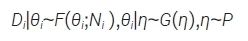
其中，Ni 表示试验的样本量，i ∈ {1,2,...,K,c}，η 为超参数。θc 的推断可以采用直接和间接两种方法。直接法MAC（meta-analytic combined） 方法[22] 在当前试验结束后直接对内外部数据进行meta 分析，得到后验分布。间接法meta 分析预测（meta-analytic predictive，MAP）先验方法[22-23] 先对外部数据进行 meta 分析得到θc的预测分布，并将其作为先验分布π(θc|D1,...,DK）；再基于Bayes 理论结合当前数据得到θc 的后验分布。 MAC 方法和 MAP 方法的后验估计通常使用混合共轭分布来近似，以使估计更加简便。

 

Schmidli 等[22] 在MAP 的基础上提出了稳健的 meta 分析预测（Robust meta-analytic predictive，rMAP） 先验方法，该方法在当前数据和外部数据存在较大差异时通过增加一项模糊先验来对外部数据进一步打折。Li 等[24] 在 rMAP 先验的基础上对二分类终点提出了经验BayesMAP（empirical Bayes meta analytic predictive，EB-MAP）先验方法，通过在先验分布上增加额外的参数来借用更多的外部数据信息。Zhang 等[25]提出了经验Bayes- 稳健-MAP（empirical Bayes robust meta analytic-predictive，EB-rMAP）先验方法，以 Box 的先验预测P 值为基础，通过一个调优参数平衡模型的简约性和灵活性来动态借用外部数据。Lin 等[26] 通过使用 Dirichlet 过程和PP 提出了一种用于网络meta 分析（network meta-analysis） 的非参数Bayes 模型。Hupf 等[27]提出了一种基于非参数Bayes方法的半参数MAP 先验，通过引入灵活的先验设定，并采用狄利克雷过程混合先验（Dirichlet process mixture prior） 更好地处理了研究间的异质性，提高了稳健性。

 

3.1.6 稳健混合先验

 

稳健混合先验（robust mixture prior，RMP）[23] 对基于外部数据得到的信息先验π1(θc|De)和弱信息先验π0(θc) 两个部分加权形成一个混合的先验分布：

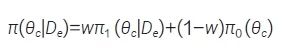
权重w控制了借用外部数据的程度。Yang 等[28] 在此基础上提出了一种自适应混合先验（self-adapting mixture，SAM），通过基于似然比检验动态调整混合权重，解决了指定混合权重的问题。

 

3.1.7 弹性先验

 

弹性先验（elastic prior，EP）方法[29] 引入了一个弹性函数g(T)，该函数根据外部数据与当前试验数据的一致性来调整信息的借用程度。其中T 是一个统计量，用来量化De 和Dc之间一致性，当θe=θc 时，T 渐近于0 ；当θe ≠ θc 时，T 渐近于无穷大。针对不同类型的试验终点，T 的选择具有灵活性，可以是适用于不同场景的统计检验量，如二项分布终点的卡方检验、正态分布终点的t 检验，以及生存分析中的log-rank 检验等。定义一个单调弹性函数g(T)，用于将 T 的值映射到 (0,1) 范围内，从而当 T趋近于0 时，g(T)趋近于1，表示可以较大程度地借用外部数据的信息；而当T 趋近于无穷大时，g(T) 趋近于0，意味着几乎不借用外部数据的信息。EP 方法的基本思想是通过调整π(θ|De) 的方差来适应性地控制信息的借用程度，该调整通过乘以 g(T)-1 来实现的。当 De 和Dc是一致的时，弹性先验 π* (θ|De) 就等同于π(θ|De)，即实现了完全信息借用。

 

3.1.8 单位信息先验

 

与其他基于似然函数构建的先验方法不同， 单位信息先验（unit information prior，UIP）方法[30-31] 直接将Fisher 信息量作为先验分布的参数，且能够根据外部数据集与当前研究的一致性或可交换性，动态调整从每个数据集中借用的信息量。UIP方法直观地解释了信息量的多少， 仅需要外部数据的汇总统计量而非个体水平数据。此外，UIP 的参数具有易于理解的含义， 使得该方法在合并多个外部数据集信息时， 能够直接应用于临床试验和观察性研究中，有效整合来自不同来源的证据，为临床决策提供更加精确和可靠的支持。

 

3.1.9 倾向性评分结合基于Bayes理论的方法

 

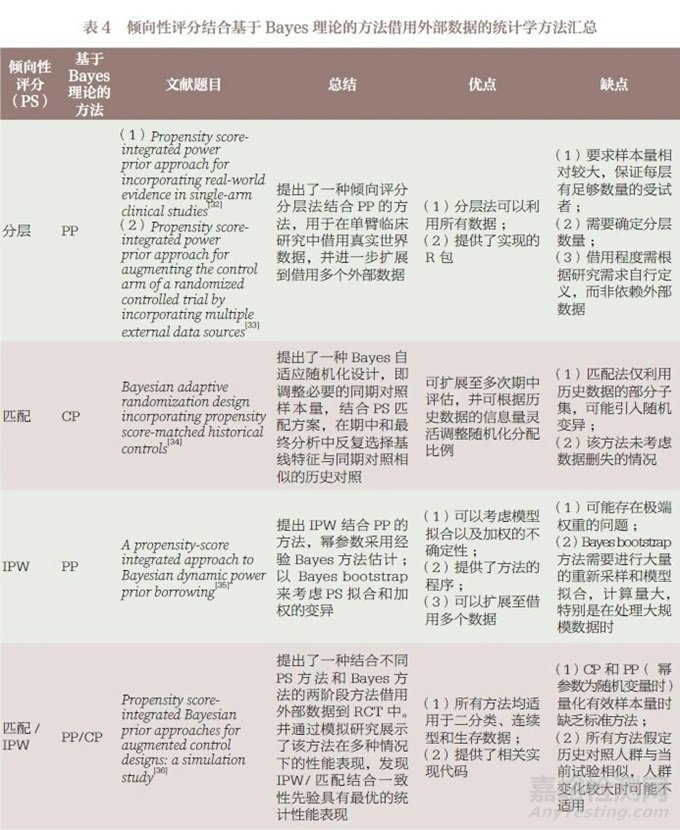
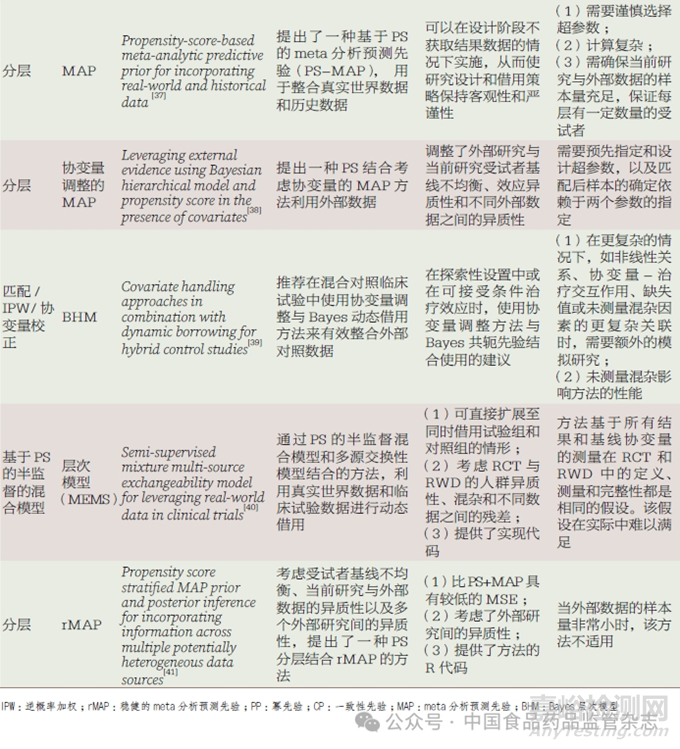
将倾向性评分（propensity score，PS）方法和基于Bayes理论的方法相结合，一方面，先利用PS 方法均衡内外部数据间的基线差异，减少基线特征差异导致的偏倚；另一方面，通过基于Bayes 理论的方法对外部数据借用程度进行打折。表4 简要汇总了近年已发表的PS 结合基于Bayes 理论的方法借用外部数据的文献，并针对各文献的研究方法和优缺点进行了讨论说明。

 

 

 

3.2 基于传统频率学派理论的方法

 

基于传统频率学派理论的方法主要包括匹配与偏倚校正、先检验后合并、PS 结合复合似然函数方法、因果估计量方法以及适应性LASSO 方法5 种方法。表5 汇总了基于传统频率学派理论方法的优缺点以及主要思想。

 

3.2.1 匹配与偏倚校正

 

匹配与偏倚校正（matching and bias adjustment） 方法[42] 假设内外部数据的潜在结局具有不同期望，其差异可反映不同研究数据的差异：

 

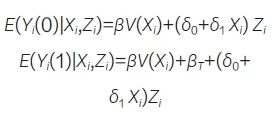
其中Yi(1) 和Yi(0) 分别表示当前研究个体i接受治疗和不接受治疗下的“潜在结局”，V(Xi) 是一个未知但单调的协变量函数，δ0 和δ1 是代表不同研究数据差异的参数，可以是常数或协变量的函数， βT 是待估参数。该方法的具体步骤如下：首先，基于PS进行匹配，先对当前研究的对照组及试验组进行匹配；然后，将当前研究试验组未成功匹配的个体与外部对照数据进行匹配；最后，再将当前对照数据与外部对照数据进行匹配。完成上述步骤后，对当前对照组与外部对照组匹配的数据拟合最小二乘法模型：

 

 

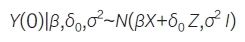
基于估计的δ̂0 对当前试验组与外部对照组匹配的数据进行调整，以扣除对照组内外部效应不一致的影响。完成上述调整后，再对所有匹配成功的数据进行合并分析。为考虑估计δ̂0 的不确定性，可基于多重填补的策略重复上述过程进行多次偏差调整和抽样，并采用Rubin 合并方法获得合并的点估计和区间估计。

 

3.2.2 先检验后合并

 

Viele 等[43] 提出了一种基于“先检验后合并（test-thenpool）”策略的频率学派方法，首先对内外部数据进行假设检验以评估是否存在统计学上的显著差异。如果差异不显著，则合并数据进行最终分析；如果差异显著，则仅使用当前研究数据。改进的“ 基于等效的先检验后合并（equivalence-based test-then-pool）”方法[44] 则通过等效性检验进行评估，不仅可检验内外部数据间是否存在差异，还考察这些差异是否小于预先设定的等效性边界。

 

3.2.3 PS 结合复合似然函数

 

Chen 等[45] 提出了一种基于研究间倾向性评分结合复合似然函数（PS-integrated composite likelihood approach） 的方法，先根据当前研究患者的PS 范围，排除RWD 中超出该范围的患者，再基于PS 分层，在每个分层内为处理组和对照组指定综合似然函数，并通过加权乘积形式调整RWD 的权重，以削弱其对整体估计的影响，最后将所有分层的估计值进行加权平均，得到整体人群的治疗效应估计。可使用重叠系数作为相似性度量来确定每个分层中RWD 的折扣参数，并使用自助法或Jackknife 方法获得治疗效应估计的方差并构建假设检验和置信区间，完成统计推断。

 

3.2.4 因果估计量方法

 

Chu 等[46] 提出， 采用内外部数据加权平均方法估计因果效应时， 应选择使得治疗效应估计的均方误差（mean square error，MSE） 最小的权重为近似最优权重，合并后的治疗效应θ 定义为：

 

 

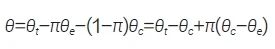
其中，π 即为权重参数，取值范围在0 到1 之间，其近似最优取值为当MSE(θ) 最小时的值。

 

Guo 等[47] 提出的因果估计量方法是通过自适应权重因子π 的形式， 动态地融合外部对照数据和当前试验数据，见公式（8）。其中，n 为总样本量，即n=Nt+Nc+Ne； π 是平衡当前对照和外部对照信息的权重，取值为当前对照样本量占当前与外部有效样本量（effective sample size）之和的占比；w0 (xi) 是考虑内外部数据基线分布不均衡后的权重。

 

 

 

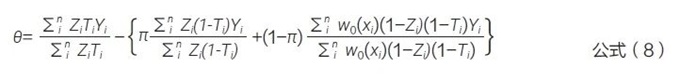
3.2.5 适应性LASSO 方法

 

Li 等[48] 借鉴了Bayes 异质性先验借用方法的思想，将其转化为频率派框架中的正则化回归问题。在这个框架下，外部数据的借用可通过一个自适应的惩罚项[ 自适应最小绝对收缩与选择算子（Least Absolute Shrinkage and Selection Operator，LASSO）] 来动态调整，以适应内外部数据之间的差异。该方法首先通过常规的统计回归方法，初步估计外部对照和当前对照数据的差异δ，根据已观测数据得到参数δ 的初步估计值δ̂0：

 

 

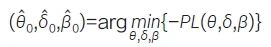
其中，θ 表示治疗效应，β 表示协变量效应。随后基于初步估计的差异δ̂0 ，动态调整模型中的正则化强度，根据目标函数估计治疗效应，见公式（9）。其中，γ和λ 是超参数，二者皆大于0。λ表示借用外部数据的程度，λ 越大提示惩罚越高，因此借用的外部数据越多；γ 表示借用程度对δ̂的适应程度，当漂移越来越大时，较大的γ 能够快速适应并降低借用度。该方法得出的治疗效应渐近服从已知分布，可以用于构建置信区间和进行假设检验。

 

 

 

 

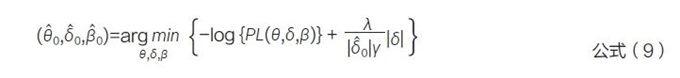
4、讨论与总结

 

RWD 的可用性为临床试验方法学带来了新的视角，通过采用创新的方法和研究设计，可以有效减少所需的样本量，缩短临床试验的时间，从而加速研发进程，尽快为患者提供有效治疗。这种探索不仅可以挖掘外部数据在克服传统临床试验局限性方面的巨大潜力，也为未来临床研究方法论的创新提供了新路径，有利于更有效地解决复杂的问题。

 

在借用外部RWD 时需要考虑数据的质量、数据的可比性、数据的适用性等一系列问题。在数据满足研究要求时，统计学方法的选择就成为了研究的焦点。通过对基于Bayes 理论的方法和基于传统频率学派理论的方法在借用外部对照数据中的应用进行比较和分析，可以看到不同方法在不同情境下的优势和局限性。基于传统频率学派理论的方法，如频数法，在简单、明确的数据情况下表现出较高的易用性和可解释性。基于经典的假设检验，为研究者提供了直观和易于理解的统计推断，但可能无法充分考虑到外部数据与当前试验数据之间的差异。相比之下，基于Bayes 理论的方法在借用外部对照数据时表现出更高的灵活性和准确性，通过引入先验信息，能够更好地结合外部数据与当前试验数据，降低外部数据的权重，并考虑数据之间的异质性。这有助于提高分析的精度和可靠性，特别是在复杂、不确定的数据情况下。然而，基于Bayes 理论的方法的应用仍然面临一些固有挑战，如先验信息的选择、模型的假设和计算复杂性等。

 

综合而言，在选择适宜的统计分析方法时，建议根据研究问题的性质、数据的特性、研究证据的支持场景（例如支持确证性研究或探索性研究）进行综合考虑。对于简单、明确的数据情况，基于传统频率学派理论的方法可能更适用；而对于复杂、不确定的数据或需要更深入分析的情况，基于Bayes 理论的方法可能更具优势。同时，也需要注意到不同方法的具体局限性和挑战，并在实际应用中灵活运用和调整，以获得更准确和可靠的研究结果。

 

引用本文

 

陈金梅,赵圆圆,朱鹏飞,陈平雁,秦国友*,吴莹*.临床试验中借用外部数据的统计学方法[J].中国食品药品监管,2024(10):10-23.