当电磁波在真空中传播时，速度为光速，这也是信息从一个地方传到另一个地方时可以达到的最大速度。如果电磁波在介质中传播，速度会降低到v＜c0.n=v/c的比值为透明介质的折射率。一种研究在可见光光谱范围的折射率的传统方法是使用棱镜观察光的色散。因为介质的折射率作为入射光波长的函数会变化，光将会产生色散。这不仅在可见光谱范围内，对于覆盖整个半无限光波场的函数会变化，光将会产生色散。这不仅在可见光谱范围内，对于覆盖整个半无限光谱范围的不同波长也是有效地。色散在一些光谱范围内，对于覆盖整个半无限光谱范围的不同波长也是有效的。色散在一些光谱范围可能会相当的弱，但在其他一些范围可能会相当强。一些由太赫兹辐射探测的材料可以观察到较强的折射率的变化。

如果我们摒弃透明介质的假设，那么吸收过程起着重要的作用。在可见光范围内，吸收光线的媒质通常有着特定的颜色。如果一个媒质通常有着特定的颜色。如果一个媒质看上去是红色，在光传输波长中显示红色的波不会衰减有着特定的颜色。如果一个媒质看上去是红色，在光传输波长中显示红色的波不会衰减或衰减作用较弱，而其他波长沿传播方向会衰减较多。光的吸收和色散是彼此紧密相连的，这种联系可以用复折射率的概念表述。复折射率是一个可观察到的量。然而，我们需要首先引入复介电常数，这是影响复折射率的主要参数。因为媒质的介电常数描述媒质的属性及其与电磁波相互作用。

从经典电磁学理论我们知道媒质电荷的极化，P和入射电场E成正比，并存在关系式：

式中:Ƹ₀是真空中介电常数；x是所谓的媒质的电极化率。上式采用标量形式，但它同样适用于各向同性条件下媒质的矢量形式。

电感应强度D是由下列公式定义：

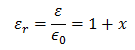
式中ɛ为媒质的介电常数。

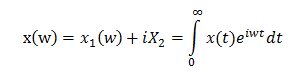
式中Ƹr为相对介电常数，是一个数值，在描述电磁场和媒质相互作用中起重要作用。

值得注意的是，我们还没有提到任何关于磁场与媒质相互作用作用的内容。因为在在本书中，太赫兹范围内磁场与媒质之间的相互作用被认为是很弱的。磁场与传统媒质的相互作用，对于像无线电波这样的，可以得到洛伦茲模型，对导体来说就是所谓的德鲁特模型。半导体的介电常数定性上来讲是洛伦茲模型，对导体来说就是所谓的德鲁特模型。半导体的介电常数定性上来讲是洛伦茲介电常数和德鲁特介电常数的和。因果关系基本规律在吸收-色散过程中发挥着重要作用。媒质的响应函数x（t）受外部场的影响可以由傅里叶变换给出：

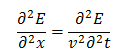
式中：w是电场的角频率；i是虚数单位。

积分的下限为零，因为系统的反应总是迟于扰动引起的响应。这就是因果关系如何影响系统响应的一个方面。由于x(t)是一个实函数，我们通过傅里叶变换得到一个复函数。相应的物理解释为方程式里面的实数部分描述的是色散，而虚数部分跟电场的吸收相关。由于磁化率是复数，这导致媒质的相对介电常数也是复数值。

为了简单起见，沿着x轴方向传播的电场的波动方程可以由下面的表达式给出：

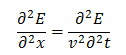
式可由麦克斯韦方程组推导得到。正如前面所述，媒质中电场的速度v取决于是折射率。因子1/v²可以用因子Ƹu替代。其中，u是媒质的磁导率。在不存在吸收的情况下，有一个简单的解，这个解为平面波。在存在吸收的情况下，需要修改折射率的概念，折射率需要用复折射率来代替，N=n+ik，这里k就是所谓的吸收系数。吸收系数描述了电场幅值衰减的强度。复折射率的定义为：

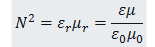
式中：ur是媒质的相对磁导率；u0为真空的磁导率。

考虑到1/v²=Ƹu,根据定义式可以明显地看出，引入复介电常数且利用太赫兹假设u=u0，复折射率可以由下式得到：

当内部磁场不同于入射场磁场时，会出现磁场损耗。为了得到复折射率，需要根据定义式引入一个复磁导率。但如前所述，这种情况应该与传统材料的低角频率是相关的，在超材料中，负实折射率通过同时调整超材料的介电常数和磁导率得到。

一条射线以ɵ1角度入射到两种不同的折射率媒质的界面，会以相同角度反射，以ɵ2角度折射。斯涅耳定律如下：

在复折射率的情况下，斯涅耳定律变成了一个包含复数的方程，很难简单表达其物理含义。

电场从左边入射，媒质在纵轴的右手边。电场的幅值沿垂直方向衰减。如果媒质是均匀的，那么我们可以应对传输有效的比尔—朗伯定律。比尔朗伯定律可以写为：

式中l0是入射强度，I 的强度在距离d处测量，α是媒质的吸收系数。上式是均匀介质中传输的光谱采用的基本方程。消光系数和吸收系数由下面公式结合起来，即：

在针对传输数据进行分析时，需要考虑辐射入射到样本上时内部和外部反射。